Integrals and Miscellaneous 16

From (Almost) Impossible Integrals, Sums, and Series(Amazon)$$\sum_{n=1}^\infty\frac{H_n^{(p)}}{n^q}+\sum_{n=1}^\infty\frac{H_n^{(q)}}{n^p}=\zeta(p)\zeta(q)+\zeta(p+q)$$PROOF.\begin{eqnarray*}\sum_{n=1}^\infty\frac{H_n^{(p)}}{n^q} &=& \sum_{n=1}^\infty\sum_{k=1}^n\frac{1}{n^q k^p} \\&=& \sum_{k=1}^\infty\sum_{n=k}^\infty\frac{1}{n^q k^p} \\&=& \sum_{k=1}^\infty\frac{1}{k^p}\sum_{n=k}^\infty\frac{1}{n^q} \\&=& \sum_{k=1}^\infty\frac{1}{k^p}\left(\zeta(q)+\frac{1}{k^q}-H_{k}^{(q)}\right) \\&=& \zeta(q)\zeta(p)+\zeta(p+q)-\sum_{k=1}^\infty\frac{H_k^{(q)}}{k^p}\end{eqnarray*}Especially setting $p=q$ yields$$\sum_{n=1}^\infty\frac{H_n^{(p)}}{n^p}=\frac{1}{2}\left(\zeta(p)^2+\zeta(2p)\right)$$

$$\int_0^1\frac{\Li_2^2(t)}{t}dt=2\zeta(2)\zeta(3)-3\zeta(5)$$PROOF.
Cauchy's product of $\Li_2$ and $\Li_2$ is\begin{eqnarray*}\Li_2^2(t) &=& t^2\sum_{n=1}^\infty\sum_{m=1}^{n}\frac{t^{n-1}}{m^2(n-m+1)^2}\end{eqnarray*}\begin{eqnarray*}\therefore\quad\int_0^1\frac{\Li_2^2(t)}{t}dt &=& \sum_{n=1}^\infty\sum_{m=1}^{n}\frac{1}{m^2(n-m+1)^2}\int_0^1 t^n dt \\&=& \sum_{n=2}^\infty\sum_{m=1}^{n-1}\frac{1}{m^2n(n-m)^2} \\&=& \sum_{n=2}^\infty\frac{1}{n^3}\sum_{m=1}^{n-1}\left(\frac{1}{m}+\frac{1}{n-m}\right)^2 \\&=& \sum_{n=2}^\infty\frac{1}{n^3}\sum_{m=1}^{n-1}\left(\frac{1}{m^2}+\frac{1}{(n-m)^2}+\frac{2}{n}\left(\frac{1}{m}+\frac{1}{n-m}\right)\right) \\&=& \sum_{n=2}^\infty\frac{1}{n^3}\left(2H_{n-1}^{(2)}+\frac{4}{n}H_{n-1}\right) \\&=& 2\sum_{n=1}^\infty\frac{H_{n-1}^{(2)}}{n^3}+4\sum_{n=1}^\infty\frac{H_{n-1}}{n^4}\end{eqnarray*}The first sum is$$\sum_{n=1}^\infty\frac{H_{n-1}^{(2)}}{n^3}=3\zeta(2)\zeta(3)-\frac{11}{2}\zeta(5)$$which I proved "2023/2/11" below. And the second is$$\sum_{n=1}^\infty\frac{H_{n-1}}{n^4}=2\zeta(5)-\zeta(2)\zeta(3)$$which we obtained here. Hence we get$$\int_0^1\frac{\Li_2^2(t)}{t}dt=2\zeta(2)\zeta(3)-3\zeta(5)$$

From @MAGNA81407795:$$\prod_{n=1}^\infty\frac{(4n+3)(4n+15)}{(4n+6)(4n+12)}=\frac{512\sqrt{\pi}}{1155\G^2(\frac{3}{4})}$$PROOF.\begin{eqnarray} LHS &=& \frac{\G(\frac{5}{2})\G(4)}{\G(\frac{7}{4})\G(\frac{19}{4})}\lim_{n\to\infty}\frac{\G(\frac{7}{4}+n)\G(\frac{19}{4}+n)}{\G(\frac{5}{2}+n)\G(4+n)}\\ &=& \frac{\G(\frac{5}{2})\G(4)}{\G(\frac{7}{4})\G(\frac{19}{4})}\tag{1} \\&=& \frac{512\sqrt{\pi}}{1155\G^2(\frac{3}{4})}\end{eqnarray}We used the lemma that suppose $\sum_{i=0}^k a_i=\sum_{i=0}^k b_i$ then$$\lim_{z\to\infty}\frac{\G(z+a_1)\G(z+a_2)\cdots\G(z+a_k)}{\G(z+b_1)\G(z+b_2)\cdots\G(z+b_k)}=1$$proved here.

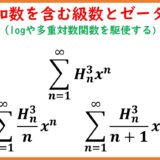
\begin{eqnarray}\sum_{n=1}^\infty\frac{H_n^{(2)}}{n^3} &=& -\frac{9}{2}\zeta(5)+3\zeta(2)\zeta(3) \\ \sum_{n=1}^\infty\frac{H_n^{(3)}}{n^2} &=& \frac{11}{2}\zeta(5)-2\zeta(2)\zeta(3)\end{eqnarray}

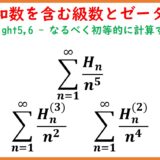
\begin{eqnarray*}\sum_{n=1}^\infty\frac{H_n}{n^5} &=& \frac{7}{4}\zeta(6)-\frac{1}{2}\zeta(5)\\\sum_{n=1}^\infty\frac{H_n^{(2)}}{n^4} &=& -\frac{1}{3}\zeta(6)+\zeta(3)^2\\\sum_{n=1}^\infty\frac{H_n^{(4)}}{n^2} &=& \frac{37}{12}\zeta(6)-\zeta(3)^2\end{eqnarray*}

\begin{eqnarray*}\sum_{k=1}^\infty\sum_{n=1}^\infty\frac{1}{n^3(n+k)^2} &=& \frac{9}{2}\zeta(5)-2\zeta(2)\zeta(3)\\\sum_{n=1}^\infty\sum_{k=1}^\infty\frac{1}{n^3(n+k)^3}&=&-\frac{1}{2}\zeta(6)+\frac{1}{2}\zeta(3)^2\\\sum_{n=1}^\infty\sum_{k=1}^\infty\frac{1}{n^4(n+k)^2}&=&\frac{25}{12}\zeta(6)-\zeta(3)^2\end{eqnarray*}PROOF here:

調和数を含んだ級数(Euler-sum)とゼータ関数 part14

Theorems:$$\int_0^1 x^{n-1}\ln(1-x)dx=-\frac{H_n}{n}$$$$\int_0^1 x^{n-1}\ln^2(1-x)dx=\frac{H_n^2+H_n^{(2)}}{n}$$$$\int_0^1 x^{n-1}\ln^3(1-x)dx=-\frac{H_n^3+3H_nH_n^{(2)}+2H_n^{(3)}}{n}$$Lemmas:$$\sum_{k=1}^n\frac{H_k}{k} =\frac{H_n^2+H_n^{(2)}}{2}$$$$\sum_{k=1}^n\frac{H_k^2+H_k^{(2)}}{k}=\frac{H_n^3+3H_nH_n^{(2)}+2H_n^{(3)}}{3}$$

Abel's transformation：
Suppose $A_n:=\sum_{k=0}^n a_k$ then$$\sum_{k=m+1}^{m+n} a_kb_k=A_{m+n} b_{m+n+1}-A_m b_{m+1}+\sum_{k=m+1}^{m+n} A_k(b_k-b_{k+1})$$

PROOF:

logを含む難しい積分10(調和数・アーベルの級数変形法)

$${}_3F_2\left[\begin{matrix}1,1,\nu+1\\2,\lambda+1\end{matrix};1\right] =\frac{\lambda}{\nu}\Bigl(\psi(\lambda)-\psi(\lambda-\nu)\Bigr)$$$${}_3F_2\left[\begin{matrix}1,1,1\\2,\lambda+1\end{matrix};1\right] =\lambda\zeta(2,\lambda)$$$${}_3F_2\left[\begin{matrix}1,1,1+a\\2,2+a\end{matrix};-1\right] = \frac{1+a}{a}\left(\psi(1+a)-\psi\left(1+\frac{a}{2}\right)\right)$$\begin{eqnarray}&&{}_4F_3\left[\begin{matrix}1,1,1+a,1+b\\2,\frac{a+3}{2},1+2b\end{matrix};1\right]\\&=&\frac{1+a}{2a}\left[\psi\left(\frac{1+a}{2}\right)-\psi\left(\frac{1}{2}\right)+\psi\left(b+\frac{1}{2}\right)-\psi\left(b+\frac{1-a}{2}\right)\right]\end{eqnarray}$${}_3F_2\left[\begin{matrix}1,1,1+a\\2,\frac{a+3}{2}\end{matrix};\frac{1}{2}\right] = \frac{1+a}{2a}\left[\psi\left(\frac{1+a}{2}\right)-\psi\left(\frac{1}{2}\right)\right]$$$${}_3F_2\left[\begin{matrix}1,1,1\\2,\frac{3}{2}\end{matrix};\frac{1}{2}\right] = \frac{\pi^2}{8}$$PROOF.

超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値１

\begin{eqnarray}&&{}_4F_3\left[\begin{matrix}1,1,1+a,1+b\\2,2+a-b,2+a\end{matrix};1\right] \\&=& \frac{(1+a)(1+a-b)}{ab}\sum_{n=1}^\infty \frac{(a)_n(b)_n}{n(1+a-b)_n(1+a)_n} \\ &=& \frac{(1+a)(1+a-b)}{ab}\left[\psi\left(1+\frac{a}{2}\right)+\psi(1+a-b)-\psi(1+a)-\psi\left(1+\frac{a}{2}-b\right)\right]\end{eqnarray}

\begin{eqnarray}&&{}_5F_4\left[\begin{matrix}1,1,1+a,2+\frac{a}{2},1+b\\2+a,2,1+\frac{a}{2},2+a-b\end{matrix};-1\right] \\&=& -\frac{(1+a)(1+a-b)}{(2+a)b}\sum_{n=1}^\infty \frac{(a)_n(1+\frac{a}{2})_n(b)_n(-1)^n}{n(\frac{a}{2})_n(1+a-b)_n(1+a)_n} \\ &=& \frac{(1+a)(1+a-b)}{(2+a)b}\left[\psi(1+a)-\psi(1+a-b)\right]\end{eqnarray}

\begin{eqnarray}&&{}_8F_7\left[\begin{matrix}1,1,1+a,1+b,1+c,2+\frac{a}{2},2+2a-b-c+m,1-m\\2,1+\frac{a}{2},2+a-b,2+a-c,2+a,1+b+c-a-m,2+a+m\end{matrix};1\right] \\&=& -\frac{(1+a)(1+a-b)(1+a-c)(b+c-a-m)(1+a+m)}{bcm(2+a)(1+2a-b-c+m)}\\&&\times\Bigl[\psi(1+a-b)+\psi(1+a-c)+\psi(1+a+m)+\psi(1+a-b-c+m)\\&&\quad\quad-\psi(1+a)-\psi(1+a-b-c)-\psi(1+a-b+m)-\psi(1+a-c+m)\Bigr]\end{eqnarray}

\begin{eqnarray}&&{}_6F_5\left[\begin{matrix}1,1,a,b,c,\frac{3+c}{2}\\2,\frac{1+c}{2},1+c,2-a+c,2-b+c\end{matrix};1\right] \\&=& \frac{c(1-a+c)(1-b+c)}{(a-1)(b-1)(c+1)}\\&&\times\Bigl[\psi(1-a+c)+\psi(1-b+c)-\psi(c)-\psi(2+c-a-b)\Bigr]\end{eqnarray}

超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値２

$$\sum_{n=1}^\infty H_n^{(p)}x^n=\frac{\Li_p(x)}{1-x}$$PROOF.
The cauthy product of the following two series:$$\Li_p(x)=\sum_{n=1}^\infty\frac{x^n}{n^p}\;,\;\frac{1}{1-x}=1+x+x^2+\cdots$$gives\begin{eqnarray*}\frac{\Li_p(x)}{1-x} &=& \left(\sum_{n=1}^\infty\frac{x^n}{n^p}\right)\left(\sum_{n=0}^\infty x^n\right) \\&=& \sum_{n=1}^\infty\left(\sum_{k=1}^n \frac{1}{k^p}\right)x^n \\&=&\sum_{n=1}^\infty H_n^{(p)}x^n\end{eqnarray*}

\begin{equation}\sum_{n=1}^\infty (H_n^2-H_n^{(2)})x^n=\frac{\ln^2(1-x)}{1-x}\tag{A}\end{equation}PROOF.
Recall the following formula$$\sum_{n=1}^\infty H_n^{(2)}x^n=\frac{\Li_2(x)}{1-x}$$proved "2023/2/18" above in this page, and $$\sum_{n=1}^\infty H_n^2x^n=\frac{\ln^2(1-x)+\Li_2(x)}{1-x}$$proved here. Then (A) follows.

$$\sum_{n=0}^\infty\frac{(2n)!!}{(2n+1)!!}\frac{(n+1)(2n+5)}{(2n+1)(2n+3)^2}=1$$$${}_4F_3\left[\begin{matrix}1,\frac{1}{2},\frac{1}{2},\frac{7}{2}\\\frac{5}{2},\frac{5}{2},\frac{5}{2}\end{matrix};1\right]=\frac{9}{5}$$

\begin{eqnarray*}{}_3F_2\left[\begin{matrix}1,1,\frac{1}{2}\\\frac{3}{2},\frac{3}{2}\end{matrix};1\right] &=& 2G\\{}_3F_2\left[\begin{matrix}1,1,\frac{3}{2}\\\frac{5}{2},\frac{5}{2}\end{matrix};1\right] &=& 18-18G\end{eqnarray*}PROOF:

4F3の特殊値の計算例（一般化超幾何級数のEuler積分表示）

$$I:=\int_0^\infty xe^{-x}\cos xdx=0$$$$J:=\int_0^\infty xe^{-x}\sin xdx=\frac{1}{2}$$PROOF. We define$$I(s):=\int_0^\infty e^{-sx}\cos xdx\;,\;J(s):=\int_0^\infty e^{-sx}\sin xdx$$to find $I=-I'(1)$ , $J=-J'(1)$. It follows from Laplace transforms that$$I(s)=\frac{s}{s^2+1}\;,\; J(s)=\frac{1}{s^2+1}$$and$$I'(s)=\frac{1-s^2}{(s^2+1)^2}\;,\; J(s)=\frac{-2s}{(s^2+1)^2}$$Hence,$$I=0\;,\;J=\frac{1}{2}$$

Simpler way: We can integrate directly.$$\int xe^{-x}\cos xdx=\frac{e^{-x}}{2}[(x+1)\sin x-x\cos x]+C$$$$\int xe^{-x}\sin xdx=-\frac{e^{-x}}{2}[(x+1)\cos x+x\sin x]+C$$

$$S:=\sum_{n=1}^\infty\frac{(-1)^n\ln n}{n}=\g\ln2-\frac{\ln^22}{2}$$PROOF.
We define $$f(s):=\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n^s}=\left(1-\frac{1}{2^{s-1}}\right)\zeta(s)$$to find $$S=\lim_{s\to0}f'(s+1)$$We obtained in the previous post that$$\displaystyle\lim_{s\to 1}\left(\zeta(s)-\frac{1}{s-1}\right)=\gamma$$Hence,$$\zeta(s)=\frac{1}{s-1}+\g+O(s-1)$$and we see easily that$$2^s=1+s\ln2+s^2\frac{\ln^22}{2}+O(s^3)$$$$\therefore\quad f(s+1)=\ln2+s\g\ln2-s\frac{\ln^22}{2}+O(s^2)$$Or$$f'(s+1)=\g\ln2-\frac{\ln^22}{2}+O(s)\xrightarrow[]{s\to 0}\g\ln2-\frac{\ln^22}{2}$$

From @Turkimath1:$$S:=\sum_{n=1}^\infty\frac{(-1)^n\ln^2 n}{n}=2\g_1\ln2+\g\ln^22-\frac{\ln^32}{3}$$PROOF.
We define $$f(s):=\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n^s}=\left(1-\frac{1}{2^{s-1}}\right)\zeta(s)$$to find $$S=-\lim_{s\to0}f''(s+1)$$We obtained in the previous post that$$\displaystyle\lim_{s\to 1}\left(\zeta(s)-\frac{1}{s-1}\right)=\gamma$$Hence,$$\zeta(s)=\frac{1}{s-1}+\g-\g_1(s-1)+O((s-1)^2)$$where $\g_1$ denotes Stieltjes constant of order 1. And we see easily that$$2^s=1+s\ln2+s^2\frac{\ln^22}{2}+s^3\frac{\ln^22}{6}+O(s^4)$$$$\therefore\quad f(s+1)=\ln2+\left(\g\ln2-\frac{\ln^22}{2}\right)s+\left(-\g_1\ln2-\frac{\g\ln^22}{2}+\frac{\ln^32}{6}\right)s^2+O(s^3)$$Differentiate twice to get$$f''(s+1)=-2\g_1\ln2-\g\ln^22+\frac{\ln^32}{3}+O(s)\xrightarrow[]{s\to 0}-2\g_1\ln2-\g\ln^22+\frac{\ln^32}{3}$$

$$\sum_{n=1}^\infty\frac{(-1)^{n-1}H_n}{n^4} = \frac{59}{32}\zeta(5)-\frac{1}{2}\zeta(2)\zeta(3)$$$$\int_0^1\frac{\ln^2x\ln^2(1+x)}{x} = -\frac{29}{8}\zeta(5)+2\zeta(2)\zeta(3)$$PROOF here:

調和数を含んだ級数(Euler-sum)とゼータ関数 part15

$$\int_0^x\frac{\ln^4 u}{1-u}du=24\Li_5(x)-24\Li_4(x)\ln x+12\Li_3(x)\ln^2x-4\ln^3x\Li_2(x)-\ln^4x\ln(1-x)$$(abbreviated) PROOF.$$LHS=\sum_{n=1}^\infty\int_0^x u^{n-1}\ln^4udu$$Integration by parts 4 times yields the equation.

Especially,$$\int_0^1\frac{\ln^4 u}{1-u}du=24\zeta(5)$$$$\int_0^\frac{1}{2}\frac{\ln^4 u}{1-u}du=24\Li_5\left(\frac{1}{2}\right)+24\Li_4\left(\frac{1}{2}\right)\ln 2+\frac{21}{2}\zeta(3)\ln^22-4\zeta(2)\ln^32+\ln^52$$

\begin{eqnarray*}\int_0^\frac{1}{2}\frac{\ln^4(1-u)}{u}du &=& 24\zeta(5)-24\Li_5\left(\frac{1}{2}\right)-24\Li_4\left(\frac{1}{2}\right)\ln 2\\&&\quad-\frac{21}{2}\zeta(3)\ln^22+4\zeta(2)\ln^32-\ln^52\\ \int_0^\frac{1}{2}\frac{\ln u\ln^3(1-u)}{1-u}du &=& 6\zeta(5)-6\Li_5\left(\frac{1}{2}\right)-6\Li_4\left(\frac{1}{2}\right)\ln 2\\&&\quad-\frac{21}{8}\zeta(3)\ln^22+\zeta(2)\ln^32\end{eqnarray*}(abbreviated proof)
The first integral can be obtained by putting $u\to 1-u$ and using the result of "2023/2/25". We easily find the second integral by IBP and using the first integral.

From @penta_math\begin{eqnarray*}\int_0^\infty\frac{\sqrt{x}}{x^3+1}dx &=& 2\int_0^1 \frac{\sqrt{x}}{x^3+1}dx \\&=& 2\sum_{n=0}^\infty(-1)^n\int_0^1 x^{3n+\frac{1}{2}}dx \\&=& \frac{2}{3}\sum_{n=0}^\infty\frac{(-1)^n}{n+\frac{1}{2}} \\&=& \frac{1}{3}\sum_{n=0}^\infty\left(\frac{1}{n+\frac{1}{4}}-\frac{1}{n+\frac{3}{4}}\right) \\&=&\frac{\psi(\frac{3}{4})-\psi(\frac{1}{4})}{3}\\&=& \frac{\pi}{3}\end{eqnarray*}

\begin{eqnarray*}&&\int_0^x\frac{\ln^2u\ln^2(1-u)}{u}du \\&=& -4\Li_5(x)+4\Li_4(1-x)\ln x-4\Li_4(x)\ln x-4\Li_4\left(\frac{x}{x-1}\right)\ln x\\&&+4\Li_3(x)\ln x\ln(1-x)-2\Li_3(1-x)\ln^2x\\&&+2\Li_2(1-x)\ln^2x\ln(1-x)+\ln^3x\ln^2(1-x)\\&&+\frac{2}{3}\ln^2x\ln^3(1-x)-\frac{1}{6}\ln x\ln^4(1-x)-2\zeta(2)\ln x\ln^2(1-x) \\&& +2\zeta(3)\ln^2x-4\zeta(4)\ln x-4\zeta(3)\ln x\ln(1-x)\\&&+4\sum_{n=1}^\infty\frac{H_n}{n^4}x^n\end{eqnarray*}

$$\int_0^1\frac{\ln^2u\ln^2(1-u)}{u}du = 8\zeta(5)-4\zeta(2)\zeta(3)$$\begin{eqnarray*}&&\int_0^\frac{1}{2}\frac{\ln^2u\ln^2(1-u)}{u}du \\&=& 4\Li_5\left(\frac{1}{2}\right)+\frac{1}{8}\zeta(5)+4\Li_4\left(\frac{1}{2}\right)\ln2+\frac{7}{4}\zeta(3)\ln^22\\&&-\frac{2}{3}\zeta(2)\ln^32-2\zeta(2)\zeta(3)-\frac{\ln^52}{15}\end{eqnarray*}

\begin{eqnarray*}&&\int_0^\frac{1}{2}\frac{\ln^2u\ln^2(1-u)}{1-u}du \\&=& -4\Li_5\left(\frac{1}{2}\right)+\frac{63}{8}\zeta(5)-4\Li_4\left(\frac{1}{2}\right)\ln2-\frac{7}{4}\zeta(3)\ln^22\\&&+\frac{2}{3}\zeta(2)\ln^32-2\zeta(2)\zeta(3)+\frac{\ln^52}{15}\end{eqnarray*}

\begin{eqnarray*}&&\int_0^1\frac{\ln^2x\ln^2(1+x)}{1+x} \\&=& 8\Li_5\left(\frac{1}{2}\right)-\frac{33}{8}\zeta(5)+8\Li_4\left(\frac{1}{2}\right)\ln2+\frac{7}{2}\zeta(3)\ln^22\\&&-\frac{4}{3}\zeta(2)\ln^32-2\zeta(2)\zeta(3)+\frac{4\ln^52}{15}\end{eqnarray*}

\begin{eqnarray*} \sum_{n=1}^\infty\frac{H_n}{n^42^n}&=& 2\Li_5\left(\frac{1}{2}\right)+\frac{1}{32}\zeta(5)+\Li_4\left(\frac{1}{2}\right)\ln2-\frac{\zeta(4)}{8}\ln2\\&&+\frac{\zeta(3)}{2}\ln^22-\frac{\zeta(2)}{6}\ln^32-\frac{1}{2}\zeta(2)\zeta(3)+\frac{\ln^52}{40}\end{eqnarray*}

PROOF：

logを含む難しい積分11(調和数とEuler sumの利用)