$$I=\int_0^{2\pi}\frac{dx}{3+2\sin x}$$
以前まったく同じ積分をワイエルシュトラス置換で求めました.
今回は定番の複素積分を使って求めようと思います.
$\sin x$ や $\cos x$ が登場する積分では $z=e^{ix}$ とおいて複素積分に持ち込むという頻出の方法があります.この置換によって三角関数は$$\cos x=\frac{e^{ix}+e^{-ix}}{2}=\frac{z+z^{-1}}{2}$$$$\sin x=\frac{e^{ix}-e^{-ix}}{2i}=\frac{z-z^{-1}}{2i}$$という有理式に書き直されます.また微小要素は$$dz=ie^{ix}dx \Longrightarrow dx=\frac{dz}{iz}$$となります.
さて $z$ の積分経路ですが,$x$ が $0\to 2\pi$ と変化するとき,$z=e^{ix}$ より $z$ は複素平面上で半径 $1$ の円を描くことが分かります.つまり $z$ の経路は複素平面の下図 $C$ となります.
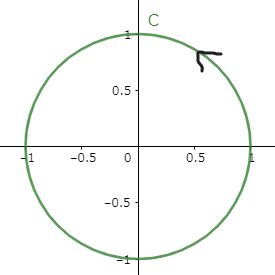
以上から求めたい積分を置換すると$$I=\oint_C\frac{1}{3+2\frac{z-z^{-1}}{2i}}\frac{dz}{iz}$$整理して$$I=\oint_C\frac{dz}{z^2+3iz-1}$$となります.ではこれをどう計算するのでしょうか?
この複素積分の被積分関数は$$f(z)=\frac{1}{z^2+3iz-1}$$です.分母が2次式になっており,その根は$$\alpha =-\frac{3-\sqrt{5}}{2}i \; ,\; \beta =-\frac{3+\sqrt{5}}{2}i$$であるため$$f(z)=\frac{1}{(z-\alpha)(z-\beta)}$$と書き換えられます.つまり $f(z)$ は $z=\alpha\; ,\;\beta$ において $1$ 位の極を持ちます(値が発散してしまうことから極と分かります。その極は分母に1次式として現れているので1位の極といいます).このうち円 $C$ の内部にあるのは $\alpha$ のみです(下図).
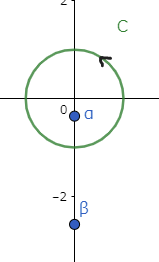
そして円の外にある $\beta$ は何と積分結果に影響を与えません.ここでは詳しく解説しませんが,周回積分のときは閉曲線の内側の領域だけ見てたらいいんだと考えてください.
さて $f(z)$ は円の内側の領域においては $z=\alpha$ に $1$ 位の極を持ちますので$$f(z)=\frac{g(z)}{z-\alpha}$$とおけば $g(z)$ は円の内側において正則な関数です.定義からもちろん$$g(z)=\frac{1}{z-\beta}$$です.$f(z)$ の分母の1位の極を表す $z-\alpha$ を取り除いたのが $g(z)$ だよというイメージですね.極を取り除かれた $g(z)$ は $z=\alpha$ まわりでふつうにテイラー展開できます.$$g(z)=a_0+a_1(z-\alpha)+a_2(z-\alpha)^2+\cdots$$これを見ると明らかに $g(\alpha) =a_0$ です.後ほど使います.
積分に話を戻します.ここまでの議論から$$I=\oint_C f(z)dz=\oint_C\frac{g(z)}{z-\alpha}dz$$従ってテイラー展開を代入すると$$I=\oint_C\left[\frac{a_0}{z-\alpha}+a_1+a_2(z-\alpha)+\cdots\right]dz$$これを項別に積分します.第1項だけ仲間外れにしておきます.\begin{equation} I=a_0\oint_C\frac{1}{z-\alpha}dz+\oint_C\left[a_1+a_2(z-\alpha)+a_3(z-\alpha)^2\cdots\right]dz\tag{1}\end{equation}
コーシーの積分定理により被積分関数が正則である2つ目の積分はゼロとなります.よって \begin{equation} I=a_0\oint_C\frac{dz}{z-\alpha}\tag{2}\end{equation} とんでもない定理で,破壊力がありますね.
(2)もまたコーシーの積分定理によって,経路を $\alpha$ を中心とする半径 $\epsilon$ の小さい円 $C'$に変更することができます.すると$z-\alpha=\epsilon e^{i\theta}$ とおいて $dz=i\epsilon e^{i\theta}d\theta$ となるので$$ I=a_0\int_0^{2\pi}\frac{i\epsilon e^{i\theta}d\theta }{ \epsilon e^{i\theta} }dz=2\pi ia_0$$
実はこれと同じ経路を(1)の段階で適用すると2つ目の積分がゼロになることを示せます.
$g(\alpha) =a_0$ でしたから$$I=2\pi i g(\alpha)=\frac{2\pi i}{\alpha -\beta}$$したがって以下の結論を得ます.
$$\int_0^{2\pi}\frac{dx}{3+2\sin x} =\frac{2\pi}{\sqrt{5}}$$
$$J=\int_0^{2\pi}\frac{dx}{2-\sin x}$$
$z=e^{ix}$ とすれば$$J=-2\oint\frac{dz}{[z-(2+\sqrt{3})i][z-(2-\sqrt{3})i]}$$経路は先ほどと同じです.円の内側にある極は $z= (2-\sqrt{3})i $ (1位)だけなのでその極を除いた関数 $$g(z)=\frac{1}{z-(2+\sqrt{3})i} $$は正則で $z= (2-\sqrt{3})i $ まわりにテイラー展開可能です.
先とまったく同様の議論で$$J=-2\cdot 2\pi ig\left( (2-\sqrt{3})i \right)=\frac{2}{\sqrt{3}}\pi$$
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。