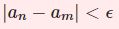今日のお役立ち文献は 藤原松三郎『数学解析第一編 微分積分学 第1巻』
任意の $\epsilon>0$ に対してある自然数 $N$ が存在し$$n>N \Rightarrow |a_n-\alpha|<\epsilon$$とできるとき、数列 ${a_n}$ は $\alpha$ に収束する。
$n$ が小さいときには $a_n$ はあまり $\alpha$ に近くないかもしれませんが、$n$ がある大きい数 $N$ より大きければ $a_n$ と $\alpha$ の差は小さくなります。つまり小さい数 $\epsilon$ を用いて $|a_n-\alpha|<\epsilon$ と書けるというわけです。
$a_n$ が限りなく $\alpha$ に近づくということは、「$\epsilon$ がどんなに小さくても$|a_n-\alpha|<\epsilon$と書ける」ことです。それが実現するのは $n$を十分大きくとったときすなわち $n>N$ のときなのです。なにか小さな数 $\epsilon$ が与えられたとき、自然数 $N$ は $|a_n-\alpha|<\epsilon$ となる $n$ の「ライン」です。どのような $\epsilon$ にたいしても、自然数 $N$ が具体的に例示できれば、$a_n$ は限りなく $\alpha$ に近づきますよ、というわけです。
※「ライン」という表現はあまり正しくないかもしれません。$N$をよぶんに大きくとれば、$n<N$でも$|a_n-\alpha|<\epsilon$となる可能性があります。
もくじ
$a_n=\frac{1}{n}$ で定義される数列は、$n\to\infty$ の極限でゼロといわれます。「分母がいくらでも大きくなるから、そりゃゼロだろう」といわれれば、雰囲気としては確かにそうだと分かるでしょう。それを「雰囲気」で終わらせずに $\epsilon$ 論法として明確化することが大事です。
$\epsilon$ 論法の概念を掴むために、次のように考えましょう。$\frac{1}{n}<0.1$ となるには、$n=100$ とすればいいです。$n$ のその先も不等式は保たれるので $n\ge 100$ ですね。すなわち「0.1という数値に対して $N=100$ と決めれば、任意の $n>N$ で $\frac{1}{n}<0.1$ とできる」。次に $\frac{1}{n}<0.01$ となるには?同様に考えると「0.01という数値に対して $N=1000$ と決めれば、任意の $n>N$ で $\frac{1}{n}<0.01$ とできる」。続けて0.001に対しては、0.0001に対しては・・・も同じようにできます。しかしこれを繰り返していては永遠に終わりがありません。
そこで、どんな数値に対しても、$1/n$ をそれより小さくできるのだということを説明するのです。0.00…01のようにゼロが $a$ 個続く値に対しては、$N$=100…00というゼロが $a+1$ 個の数を決めれば、任意の $n>N$ で $\frac{1}{n}<0.00\dots01$ とできるでしょう。
考え方はこのような感じです。実際には「任意の $\epsilon>0$ に対して $N>\frac{1}{\epsilon}$ なる自然数 $N$ を決めれば、任意の $n>N$ で $\frac{1}{n}<\epsilon$ とできる」という主張になります(不等式の計算をして確認しましょう)。$\epsilon$ は任意に小さい数なのですから、よって$\frac{1}{n}$ の極限はゼロというわけです。
$a_n=\displaystyle\frac{1}{n^2}$ は 0 へ収束する.
任意の $\epsilon>0$ に対してどのように $N$ をとればよいかを考えます。ですので $N$ は $\epsilon$ に依存します。$n>N$ として$$|a_n-0|=\frac{1}{n^2}<\frac{1}{N^2}\le\frac{1}{N}$$よって $\epsilon$ に対し $N\ge1/\epsilon$ となるような $N$ を適当に選ぶことにします。そうすると確かに$$|a_n-0|=\frac{1}{n^2}<\frac{1}{N^2}\le\frac{1}{N}\le\epsilon$$従って次のようにいえるので0へ収束します。
任意の $\epsilon>0$ に対して $N\ge1/\epsilon$ なる自然数 $N$ が存在し $$n>N \Rightarrow |a_n-0|<\epsilon$$とできる。
別解として、具体的な $N$ の値を決めるケースもあげておきます。天井関数を用いて$$N=\lceil\displaystyle\frac{1}{\sqrt{\epsilon}}\rceil$$とすれば $n>N$ に対し$$|a_n-0|=\frac{1}{n^2}<\frac{1}{N^2}=\frac{1}{\lceil\displaystyle\frac{1}{\sqrt{\epsilon}}\rceil^2}\le\epsilon$$となります。
$a_n=\displaystyle\frac{n-1}{2n+3}$ は$ 1/2$ へ収束する.
任意の $\epsilon>0$ に対して$$N=\left\lceil\displaystyle\frac{5}{\epsilon}\right\rceil$$ととると、$n>N$ ならば$$ |a_n-\frac{1}{2}|=\frac{5}{4n+6}<\frac{5}{n}<\frac{5}{N}\le\frac{5}{5/\epsilon}=\epsilon$$となって証明できました。
そもそもの$N$の見つけ方ですが、$$ |a_n-\frac{1}{2}|<\cdots<\cdots$$と評価していき、$最右辺(Nの式)=\epsilon$ とか $最右辺(Nの式)<\epsilon$ などと立式して $N=(\epsilonの式)$ とするといいです。
$a_n=n^{\frac{1}{n}}$ は $1$ に収束する.
\begin{eqnarray*}\left(1+\sqrt{\frac{2}{n}}\right)^n&=&1+n\sqrt{\frac{2}{n}}+\frac{n(n-1)}{2}\frac{2}{n}+\cdots\\&>&1+\sqrt{2n}+(n-1)\\&=&n+\sqrt{2n}\\&>& n\end{eqnarray*}$$\therefore\; n^{\frac{1}{n}}<1+ \sqrt{\frac{2}{n}} $$
任意の $\epsilon>0$ に対して $N\epsilon>2$ なる $N$ をとると、$n>N$ ならば\begin{eqnarray*}|n^{\frac{1}{n}}-1|&<& \sqrt{\frac{2}{n}} < \sqrt{\frac{2}{N}}\\&<&\frac{2}{N}<\epsilon \end{eqnarray*}
私は初めて $\epsilon-N$ 論法や $\epsilon-\delta$ 論法を勉強したときには何をやっているのかよく分かりませんでした。のちに再勉強し、いろいろ例題を作って解いてみたり、逆に収束しないことを示したりしていくうちに何となくイメージができてきた感じです。そうなるとだんだん面白くなってくるので、つまづいている方はあきらめずに学習して欲しいと思います。
冒頭の否定をとることで、次の文章ができます。
ある $\epsilon>0$ をとると、任意の自然数 $N$ に対して $n>N$ かつ$$|a_n-\alpha|\ge\epsilon$$なる $n$ が存在するとき、数列 ${a_n}$ は $\alpha$ に収束しない。
ある正の数 $\epsilon$ を定めたとき、$n$ をどんなに大きくしても $|a_n-\alpha|\ge\epsilon$ となってしまう $n$ があるよということです。
といってもあんまり使い道はなさそうな定理です。「$\alpha$ に収束しないことを示せ」ではなく、単に「収束しないことを示せ」という問いの方が多いでしょう。その場合はコーシー列の否定を使う方法があります。
$a_n=\displaystyle\frac{1}{n^2}$ は $\dfrac{1}{2}$ に収束しない。
$\epsilon=1/4$ ととります。$n$ を1より大きい自然数とすると$$\left|\frac{1}{n^2}-\frac{1}{2}\right|=\frac{1}{2}-\frac{1}{n^2}\ge\frac{1}{4}=\epsilon$$よって収束しません。
$a_n=(-1)^n$ は $-1$ に収束しない。
$\epsilon=2$ ととります。任意の自然数 $N$ に対して $n=2N\:(>N)$ とすると$$|(-1)^n+1|=2\ge\epsilon$$よって収束しません。
$a_n$ と $b_n$ の極限が分かっている場合、次の定理が便利です。
$a_n\to\alpha$ , $b_n\to\beta$ のとき、
(1) $a_n+b_n\to \alpha+\beta$ ,
(2) $a_nb_n\to\alpha\beta$.
引き算・割り算も同様。
【証明】(1)について。条件より任意の $\epsilon>0$ に対して自然数 $N$ が存在して $\forall n>N$ に対し$$|a_n-\alpha|<\frac{\epsilon}{2}\;,\;|b_n-\beta|<\frac{\epsilon}{2}\quad※$$したがって\begin{eqnarray*}|a_n+b_n-(\alpha+\beta)|&<&|a_n-\alpha|+|b_n-\beta|\\ &<& \frac{\epsilon}{2}+\frac{\epsilon}{2}\\ &=&\epsilon\end{eqnarray*}
(2)について。条件より正の数 $1$ に対して自然数 $N_0$ が存在して$$|b_n-\beta|<1\quad(\forall n>N_0)$$\begin{equation}\therefore\quad |b_n|<1+|\beta|\quad(\forall n>N_0)\tag{1}\end{equation}また任意の $\epsilon>0$ に対して自然数 $N_1$ が存在して $\forall n>N_1$ に対し\begin{equation}|a_n-\alpha|<\frac{\epsilon}{1+|\alpha|+|\beta|}\;,\;|b_n-\beta|<\frac{\epsilon}{1+|\alpha|+|\beta|}\quad※\tag{2}\end{equation}さて任意の $\epsilon>0$ に対して$N=\max\{N_0,N_1\}$ とすると $\forall n>N$ に対して(1)(2)は同時に成立するので\begin{eqnarray*}|a_nb_n-\alpha\beta| &=& |a_nb_n-\alpha b_n+\alpha b_n-\alpha\beta| \\ &<& |b_n||a_n-\alpha|+|\alpha||b_n-\beta| \\ &<& (1+|\beta|)\frac{\epsilon}{1+|\alpha|+|\beta|}+|\alpha|\frac{\epsilon}{1+|\alpha|+|\beta|}\\ &=& \epsilon\end{eqnarray*}
【証明終】
※収束するなら任意の正の数で押さえられるという話でしたから、$\frac{\epsilon}{2}$ や $\frac{\epsilon}{1+|\alpha|+|\beta|}$ と書いてOK
なお逆は成り立ちません。例えば $a_n=n$ , $b_n=-n$ とすると $a_n+b_n\to0$ ですが、それぞれの数列は発散します。
$a_n\to\alpha$ , $b_n\to\beta$ , $a_n<b_n$ のとき $\alpha\le\beta$ である(等号注意!)
【証明】$c_n=a_n-b_n$とすると $c_n<0$. 定理2.1より $c_n\to\alpha-\beta$ なので $\alpha\le\beta$.【証明終】
等号に違和感あるかもしれませんが、例えば $a_n=-1/n$ , $b_n=1/n$ を考えるといいです。
$a_n\to\alpha$ , $|a_n-b_n|\to0$ ならば $b_n\to\alpha$ であることを示せ.
【解答】$\forall\epsilon>0,\exists N\in\NN$ , $\forall n>N$ , $$|a_n-\alpha|<\frac{\epsilon}{2}\;,\;|a_n-b_n|<\frac{\epsilon}{2}$$これらを用いると\begin{eqnarray*}|b_n-\alpha| &=& |b_n-a_n+a_n-\alpha| \\ &<&|a_n-b_n|+|a_n-\alpha| <\epsilon\end{eqnarray*}
高等学校で学んだはさみうちの原理を $\epsilon$ 論法で示してみましょう。
$a_n<c_n<b_n$ , $a_n\to\alpha$ , $b_n\to\alpha$ ならば $c_n\to\alpha$ である。
【証明】条件より $\forall\epsilon>0$ に対して自然数 $N$ が存在して、$\forall n>N$ で$$-\epsilon<a_n-\alpha<c_n-\alpha<b_n-\alpha<\epsilon$$$$\therefore\quad|c_n-\alpha|<\epsilon$$【証明終】
集合や数列の有界性や上限・下限についての知識が前提となります。こちらを参照:
単調増加(減少)数列が上に(下に)有界ならば、常に極限をもつ。ただし単調増加数列とは$$a_1\le a_2\le\cdots\le a_n\le\cdots$$なる数列のことである。
【証明】単調増加数列 $\{a_n\}$ が上に有界であるとすると、この数列は上限 $L$ をもつ。よって$$\forall\epsilon>0,\exists N\in\NN,a_N>L-\epsilon$$$$\therefore\quad L-\epsilon<a_N\le L$$$\forall n> N$ について単調性より $a_N\le a_n$ なので $$L-\epsilon<a_n\le L\quad\quad\therefore\quad |a_n-L|<\epsilon$$これは $\displaystyle\lim_{n\to\infty}a_n=L$ を示す。単調減少数列についても同様に示せる。【証明終】
極限値を求めることは難しくても、場合によってはこの定理によって収束することだけ示すことができます。例題を見ていきましょう。
$a_1=\sqrt{2}$ , $a_2=\sqrt{a_1}$ , $a_3=\sqrt{a_2},\cdots$ なる数列について
(1) 任意の自然数 $n$ で $a_n>1$ を示せ。
(2) 定理4.1により極限を持つことを示せ。
(3) 極限は $1$ であることを示せ。
【解答】
(1) 数学的帰納法により確かめられる(略)。
(2) $a_{n+1}^2=a_n$ であるが、(1)より $a_{n+1}>1$ なので $a_{n+1}<a_{n}$ である。よって単調減少数列かつ下に有界。定理4.1により極限をもつ。
(3) 一般項は $a_n=2^{\frac{1}{2^n}}$ である。$\forall\epsilon>0$ に対し $2^N\log_2(1+\epsilon)>1$ なる自然数 $N$ を1つ定めると $\forall n>N$ において $|a_n-1|<\epsilon$ .
【解答終】
(3)の解答はもっと簡略化して、「極限値を $\alpha$ とすると $\alpha=\sqrt{\alpha}$ なので $\alpha=1$ 」でもいいです。
$a_1=a>0$ , $a_2=a+\dfrac{1}{a_1}$ , $a_3=a+\dfrac{1}{a_2},\cdots$ なる数列について
(1) $\{a_{2n}\}$ および $\{a_{2n+1}\}$ は極限をもつことを示せ。
(2) (1)の2つの数列の極限が一致することを示し $\displaystyle\lim_{n\to\infty}a_n$ を求めよ。
【解答】
(1) 漸化式より明らかに $a_n\ge a$ である。すると $a_n=a+\frac{1}{a_{n-1}}\le a+\frac{1}{a}$ となるので\begin{equation}a\le a_{n}\le a+\frac{1}{a}\tag{A}\end{equation}また$$a_{n+2}-a_n=-\frac{a_{n+1}-a_{n-1}}{a_{n+1}a_{n-1}}$$が成り立つことから $n=1,2,3\cdots$ と順次代入することにより\begin{equation}a_1<a_3<a_5<\cdots\quad,\quad a_2>a_4>a_6>\cdots\tag{B}\end{equation}(A)(B)より$\{a_{2n}\}$ と $\{a_{2n+1}\}$ は有界かつ単調であり、定理4.1より極限をもつ。
(2) $a_{2n}\to\alpha$ , $a_{2n+1}\to\beta$ とする。$\forall\epsilon>0$ に対して自然数 $N$ が存在して、$\forall n>N$ で$$|a_{2n}-\alpha|<\epsilon\quad,\quad |a_{2n+1}-\beta|<\epsilon$$とできる。後者の等式は漸化式より$$\left|\frac{1}{a_{2n}}-(\beta-a)\right|<\epsilon$$と書き直せるため $\dfrac{1}{a_{2n}}\to \beta-a$ であることが分かる。すなわち $a_{2n}\to\dfrac{1}{\beta-a}$ なので $\dfrac{1}{\beta-a}=\alpha$. これと全く同様に $\dfrac{1}{\alpha-a}=\beta$ であり、連立させて解くと $$\alpha=\beta=\frac{a+\sqrt{a^2+4}}{2}$$よって$$\displaystyle\lim_{n\to\infty}a_n=\frac{a+\sqrt{a^2+4}}{2}$$
【解答終】
$0<b<a$ なる定数 $a,b$ がある。\begin{eqnarray*}a_1 = \frac{a+b}{2}\;,\;a_2=\frac{a_1+b_1}{2}\;,\;a_3=\frac{a_2+b_2}{2}\;,\cdots \\ b_1=\sqrt{ab}\;,\; b_2=\sqrt{a_1b_1}\;,\; b_3=\sqrt{a_2b_2}\;,\cdots\end{eqnarray*}で $a_n$ , $b_n$ を定めるとき
(1) $\{a_{n}\}$ および $\{b_{n}\}$ は極限をもつことを示せ。
(2) (1)の2つの数列の極限が一致することを示せ。
【解答】
(1) 高校数学の「相加・相乗平均」に関する不等式から $b<b_1<a_1<a$ である。同様に繰り返すと$$b<b_1<b_2<\cdots<b_n<a_n<\cdots<a_2<a_1<a$$よって $\{a_{n}\}$ と $\{b_{n}\}$ は単調かつ有界であり、定理4.1より極限をもつ。
(2) それぞれの極限を $\alpha$ , $\beta$ とおく。$\forall\epsilon>0$ に対して自然数 $N$ が存在して、$\forall n>N$ で$$|a_{n+1}-\alpha|<\frac{\epsilon}{2}\quad,\quad |b_{n}-\beta|<\epsilon$$とできる(前者:$n$ で成り立つのだから $n+1$ でも当然成り立つ)。前者は漸化式により$$\left|\frac{a_n+b_n}{2}-\alpha\right|<\frac{\epsilon}{2}\Longrightarrow \left|a_n+b_n-2\alpha\right|<\epsilon$$よって $a_n+b_n\to 2\alpha$ である。定理2.1より $\alpha+\beta=2\alpha$ となるから $\alpha=\beta$ である。
【解答終】
$n\to\infty$ で極限を持つ数列 $\{a_n\}_{n=1}^\infty$ は有界です。「$n\to\infty$ で極限をもっても、途中で発散してまた帰ってくることもあるのでは?」という疑問はこれで解決。
収束数列は有界である。
【証明】収束するから$\forall\epsilon>0$ ,$\exists N\in\NN$ , $\forall n>N$ , $|a_n-\alpha|<\epsilon$ と書ける。すなわち$$\alpha-\epsilon<a_{N+1},a_{N+2},\cdots<\alpha+\epsilon$$なので $\{a_{N+1},a_{N+2},\cdots\}$ は有界数列である。
また$\{a_1,a_2,\cdots,a_{N}\}$ はそれらの最大最小の範囲内に収まっているので有界。したがって $\{a_n\}$ は有界。【証明終】
※ 数列は前提として任意の $n$ で値をもっています。$a_n=\dfrac{1}{n-5}$ は $n\to\infty$ でゼロに収束しながら $n=5$ で無限大ではないかと考えるのは誤りです。それは数列が発散しているのではなく、$a_5$ は値を持ちませんのでそもそも数列を構成できません。
$\{a_n\}$ の極限を $\alpha$ とすると、$\{a_n\}$ の部分列の極限はすべて $\alpha$ である。
なお部分列とは $\{a_n\}$ の順番をかえずに、その一部を無限個取り出したものである.
【証明】条件より$\forall\epsilon>0$ ,$\exists N\in\NN$ , $\forall n>N$ , $|a_n-\alpha|<\epsilon$ . ここで部分列を $\{a_{n_1},a_{n_2},\cdots\}$ とする($n_1<n_2<\cdots$)。$n_k>N$ なる $k$ をとれば $\forall p>k$ に対して $|a_{n_p}-\alpha|<\epsilon$ となる。【証明終】
例えば $a_n\to2$ なら、その部分列 $a_{2n}\to2$ となります。
$a_n>0$ とするとき、$$\lim_{n\to\infty}\frac{a_{n+1}}{a_n}=L \Longrightarrow \lim_{n\to\infty}\sqrt[n]{a_n}=L$$を示せ。
【証明】条件より$\forall\epsilon>0$ ,$\exists N\in\NN$ , $\forall n>N$ , $$\left|\frac{a_{n+1}}{a_n}-L\right|<\epsilon$$したがって$$L-\epsilon<\frac{a_{n+1}}{a_n}<L+\epsilon$$ここで$$a_n=a_N\frac{a_{N+1}}{a_N}\frac{a_{N+2}}{a_{N+1}}\cdots\frac{a_n}{a_{n-1}}$$を用いると$$a_N(L-\epsilon)^{n-N}<a_n<a_N(L+\epsilon)^{n-N}$$$$\therefore\quad \sqrt[n]{a_N}(L-\epsilon)^{1-\frac{N}{n}}<\sqrt[n]{a_n}<\sqrt[n]{a_N}(L+\epsilon)^{1-\frac{N}{n}}$$
$N$ は固定されており、$n$ を大きくしていくと $L-\epsilon<\sqrt[n]{a_n}<L+\epsilon$ で押さえられます。
【証明終】
ここで特に $a_n=n$ とすると $$\lim_{n\to\infty}\sqrt[n]{n}=1$$を得ます。
今回は極限値 $\alpha$ が分かっているていでの $\epsilon$ 論法を説明しました。でも実際は極限値が分からないけど収束することを示したいこともあります。そんなときにはコーシー列を使うのですが、それはまた次回に。
数列の上極限と下極限については:
数列の和に関する面白い定理:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。