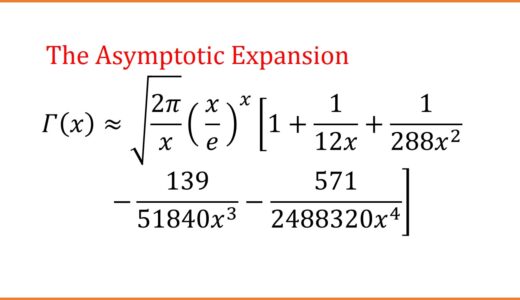「ガンマ関数の基礎」シリーズ第19回です。今日は「ビネ(Binet)の第2公式」を導出します。前回はこちら:
今日のテーマ
$\mathfrak{R}z>0$ として$$\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi+2\int_0^\infty\frac{\arctan\frac{t}{z}}{e^{2\pi t}-1}dt$$
これが今日のテーマです。以前ビネの第1公式を導出しました。第1公式は次の式です。
$$\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi+\int_0^\infty\left(\frac{1}{e^t-1}-\frac{1}{t}+\frac{1}{2}\right)e^{-zt}\frac{dt}{t}$$
第2公式をこれと見比べると、右辺の積分項だけが違っています。第1公式の積分項は $1/z$ のオーダーであり、$z$ が大きければこれを無視した式$$\log\G(z)\approx\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi$$が成り立つよっていう話でした。よって第2公式でも同様のことが言えます。
じゃあ何でわざわざ第2公式をやるの?と思うのですが、第2公式の積分項を計算することで得られる「スターリング級数」からガンマ関数の漸近公式を得ることができます(次回)。そのためのステップとして本公式を導出しましょう。
なお複素関数を扱っていますが、(4)を導出した後は、$z$ を実数と見れば高校数学で理解可能です。
アベル・プラナの和公式
Whittaker-Watsonの12章で書かれた方法を参考にします。そこではアベル・プラナの和公式を利用しています。アベル・プラナの和公式についてはこちら:
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
\begin{multline}\sum_{k=m}^nf(k)=\frac{f(m)+f(n)}{2}+\int_m^nf(z)dz\\+i\int_0^\infty\frac{f(m+iy)-f(m-iy)-f(n+iy)+f(n-iy)}{e^{2\pi y}-1}dy\end{multline}
$f(z)$ はどんな関数でもいいというわけではありませんが、少なくとも今から適用する関数については問題ありません。
ポリガンマ関数
ガンマ関数の対数をとって微分したものをディガンマ関数 $\psi(z)$ といいます。$$\psi(z)\equiv\frac{d}{dz}\log\G(z)$$これをさらに微分して得られる $\psi'(z)$ は次のように級数表示されます。
\begin{equation}\psi'(z)=\frac{d^2}{dz^2}\log\G(z)=\sum_{m=0}^\infty\frac{1}{(z+m)^2}\tag{2}\end{equation}
これについては次の過去記事をご参照:
ではスタートです。アベル・プラナの和公式の $f(\a)$ を次の関数とします。\begin{equation}f(\a)\equiv\frac{1}{(z+\a)^2}\quad(\mathfrak{R}z>0,\mathfrak{R}\a\ge0)\tag{3}\end{equation}適用する和の範囲は $m=0$ から $n=\infty$ までです。
$\a=x+iy$ とします。(3)より $f(0)=1/z^2$ , $\displaystyle\lim_{n\to\infty}f(n)=0$ , $\displaystyle\lim_{n\to\infty}f(n\pm iy)=0$ なので和公式は$$\sum_{k=0}^\infty f(k)=\frac{f(0)}{2}+\int_0^\infty\frac{1}{(z+\a)^2}d\a+i\int_0^\infty\frac{f(iy)-f(-iy)}{e^{2\pi y}-1}dy$$と、だいぶ見やすくなります。$$f(0)=\frac{1}{z^2}$$$$f(iy)-f(-iy)=-\frac{4iyz}{(z^2+y^2)^2}$$より$$\sum_{n=0}^\infty\frac{1}{(z+n)^2}=\frac{1}{2z^2}+\int_0^\infty\frac{d\a}{(z+\a)^2}+i\int_0^\infty\frac{-4iyz}{(e^{2\pi y}-1)(z^2+y^2)^2}dy$$(2)より
\begin{equation}\frac{d^2}{dz^2}\log\G(z)=\frac{1}{2z^2}+\frac{1}{z}+\int_0^\infty\frac{4tz}{(z^2+t^2)^2}\frac{dt}{e^{2\pi t}-1}\tag{4}\end{equation}
対数ガンマ関数 $\log\G(z)$ が現れました!これで準備完了です。
積分の実行
$\log\G(z)$ を導出するには(4)を2度 $z$ で積分する必要があります。$1$ から $z$ の範囲で積分すると、定数 $C$ として$$\frac{d}{dz}\log\G(z)=-\frac{1}{2z}+\log z-2\int_0^\infty \frac{1}{z^2+t^2}\frac{tdt}{e^{2\pi t}-1}+C$$と表せます。なお積分順序を交換可能であることを認めています。
もう1度 $1$ から$z$ で積分しますが $\arctan$ の扱いは注意が必要です。一般の複素数 $u$ においては次のように定義されます。$$\arctan u\equiv\int_0^u\frac{dz}{1+z^2}$$これに従い慎重に計算します。\begin{eqnarray*}\int_1^z\frac{dz}{z^2+t^2}&=&\frac{1}{t}\int_{\frac{1}{t}}^{\frac{z}{t}}\frac{d\a}{1+\a^2}\quad(z=t\a)\\&=&\frac{1}{t}\int^t_{\frac{t}{z}}\frac{d\b}{1+\b^2}\quad(\b=\frac{1}{\a})\\&=&\frac{1}{t}\left(\arctan t-\arctan\frac{t}{z}\right)\end{eqnarray*}
したがって$$\log\G(z)=-\frac{1}{2}\log z+(z\log z-z)-2\int_0^\infty\frac{\arctan t-\arctan\frac{t}{z}}{e^{2\pi t}-1}dt+Cz+C'$$$-2\int\frac{\arctan t}{e^{2\pi t}-1}dt$ も定数に含めてしまえば
\begin{equation}\log\G(z)=\left(z-\frac{1}{2}\right)\log z+(C-1)z+C^{\prime\prime}+2\int_0^\infty\frac{\arctan\frac{t}{z}}{e^{2\pi t}-1}dt\tag{5}\end{equation}
定数の決定
(5)の定数 $C,C^{\prime\prime}$ を決定しましょう。移項して絶対値をとります。$$\left|\log\G(z)-\left(z-\frac{1}{2}\right)\log z-(C-1)z-C^{\prime\prime}\right|=2\left|\int_0^\infty\frac{\arctan\frac{t}{z}}{e^{2\pi t}-1}dt\right|$$いま $z$ を正の実数とすると $t/z$ も正の実数です。よって$$0\le\arctan\frac{t}{z}\le\frac{t}{z}$$
$x>0$ として\begin{eqnarray*}x-\arctan x&=&\int_0^xdx-\int_0^x\frac{dx}{1+x^2}\\&=&\int_0^x\frac{x^2}{1+x^2}dx\ge0\end{eqnarray*}$$\therefore\quad\arctan x\le x$$
これを使って積分項を評価すると\begin{eqnarray*}\left|\int_0^\infty\frac{\arctan\frac{t}{z}}{e^{2\pi t}-1}dt\right|&=&\int_0^\infty\frac{\arctan\frac{t}{z}}{e^{2\pi t}-1}dt\\&\le&\frac{1}{z}\int_0^\infty\frac{t}{e^{2\pi t}-1}dt\\&\le&\frac{1}{z}\int_0^\infty\frac{t}{2\pi t+2\pi^2t^2+\frac{4}{3}\pi^3t^3}dt\\&=&\frac{1}{z}\int_0^\infty\frac{dt}{2\pi +2\pi^2t+\frac{4}{3}\pi^3t^2}\\\longrightarrow&& 0\quad(as\quad z\to\infty)\end{eqnarray*}よって$$\displaystyle\lim_{z\to\infty}\left|\log\G(z)-\left(z-\frac{1}{2}\right)\log z-(C-1)z-C^{\prime\prime}\right|=0$$
冒頭で紹介したビネの第1公式の積分項は $1/z$ のオーダーですから$$\displaystyle\lim_{z\to\infty}\left|\log\G(z)-\left(z-\frac{1}{2}\right)\log z+z-\frac{1}{2}\log2\pi\right|=0$$見比べると $C=0$ , $C^{\prime\prime}=\frac{1}{2}\log2\pi$ です。
(5)にこの定数値を代入して、ようやく目的の式を導出できました!
$\mathfrak{R}z>0$ として$$\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi+2\int_0^\infty\frac{\arctan\frac{t}{z}}{e^{2\pi t}-1}dt$$
例題はたとえばここの「2023/1/31B」、ここの「2022/4/7」、ここの「2022/3/31」「2022/4/3」「2022/4/5」
こちらの記事でみたように、アベル・プラナの和公式にはバリエーションがあります。これを応用すると、ビネの第2公式と類似した式$$\ln\G\left(z+\frac{1}{2}\right)=z\ln z-z+\frac{\ln2\pi}{2}-2\int_0^\infty\frac{\arctan\frac{t}{z}}{e^{2\pi t}+1}dt$$を得ます。詳しくはその記事をどうぞ。
特に $z=1$ なら
$$\int_0^\infty\frac{\arctan x}{e^{2\pi x}+1}dx=\frac{3}{4}\ln 2-\frac{1}{2}$$
アベル・プラナの和公式からのスタートだったので、なかなか大変でした。
$z>0$ として$$\displaystyle\lim_{z\to\infty}\left|\log\G(z)-\left(z-\frac{1}{2}\right)\log z+z-\frac{1}{2}\log2\pi\right|=0$$が成り立つので、 $z\to\infty$ によって $$\log\G(z)\approx\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi$$でした。これの指数をとると$$\G(z)\approx\sqrt{\frac{2\pi}{z}}\left(\frac{z}{e}\right)^z$$となります。「スターリングの近似」として有名な式です。
次回はこのことをより詳しく見ていきます。 $\log\G(z)$ を漸近展開して「スターリング級数」を導出し、「ガンマ関数の漸近公式」を作りましょう。
次回:
過去には「ビネの第1公式」も導出しています。本シリーズにおいては:
高校数学で理解できる導出方法はこちらの2本立て:
本シリーズを1から学ぶ場合は第1回をご覧ください:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。