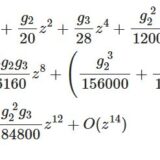前回はこちら:
前回は一般的な楕円関数の定義と性質を見ました。定数でない楕円関数の位数は2以上なので、もっとも単純な楕円関数の位数は2となります。このような楕円関数の1つとして
2位の極を1つもち、その留数がゼロである。
ようなものが考えられます。どんな関数なのでしょう。これが今回のテーマです。
$m,n$ について和をとる二重級数を次のように書くことにします。\begin{align}\sum_{m,n}&:=\sum_{m=-\infty}^\infty\sum_{n=-\infty}^\infty\tag{1a}\\\sum_{m,n}'&:=\underset{(m,n)\neq(0,0)}{\sum_{m=-\infty}^\infty\sum_{n=-\infty}^\infty}\tag{1b}\end{align}両式とも二重級数を表しますが(1b)のほうは $m,n$ が共にゼロとなる場合を省いています。(1a)(1b)の右辺は $n$ のシグマを後ろに置いていますが、$n$ の総和を先にとることを必ずしも意味しません。実際、今回扱う級数は絶対収束するので足し上げる順は任意です。二重級数の詳しい理論についてはこちらを見てください。
ゼロでない $\o_1,\o_2\in\CC$ を考えます。この2つの複素数の比は実数でないとします。そして\begin{equation}\wp(z):=\frac{1}{z^2}+\sum_{m,n}'\left[\frac{1}{(z-m\o_1-n\o_2)^2}-\frac{1}{(m\o_1+n\o_2)^2}\right]\tag{2a}\end{equation}なる関数を定義します。これをワイエルシュトラスのペー関数といいます。簡単のために$$\O_{m,n}:=m\o_1+n\o_2$$とおくと\begin{equation}\wp(z):=\frac{1}{z^2}+\sum_{m,n}'\left[\frac{1}{(z-\O_{m,n})^2}-\frac{1}{\O_{m,n}^{~2}}\right]\tag{2b}\end{equation}(1b)で確認した通り、級数は $m,n$ がともにゼロの場合を除いて和をとっています。
$\wp(z)$ は関数項の級数として定義されていますので、収束性を調べる必要があります。絶対収束であれば和をとる順番を自由に変えられますし、一様収束であれば項別微分ができます。実際、この級数は絶対一様収束することをこれから示しましょう。
整数 $m,n$ の絶対値が十分に大きければ $|z|$ に対して $|\O_{m,n}|$ は大きくなります。すると\begin{align}\left|\frac{1}{(z-\O_{m,n})^2}-\frac{1}{\O_{m,n}^{~2}}\right|&= \frac{1}{|\O_{m,n}|^2}\left|\frac{1}{(1-\frac{z}{\O_{m,n}})^2}-1\right|\\&=\frac{1}{|\O_{m,n}|^2}\left|1+2\frac{z}{\O_{m,n}}+O\left(\frac{1}{\O_{m,n}^2}\right)-1\right|\\&=O\left(\frac{1}{|\O_{m,n}|^3}\right)\end{align}よって(2b)の絶対収束性を調べるために$$\sum_{m,n}'\frac{1}{|\O_{m,n}|^3}$$の収束性を調べることにします。
$\o_1=\a_1+i\b_1$ , $\o_2=\a_2+i\b_2$ のように実部と虚部にわけます。$\o_1$ と $\o_2$ の比が実数でないことから $\a_1\b_2-\a_2\b_1\neq0$ です。実数 $s>0$ に対し\begin{align*}\frac{1}{|\O_{m,n}|^s}&=\frac{1}{|\a_1m+i\b_1m+\a_2n+i\b_2n|^s}\\&=\frac{1}{|(\a_1m+\a_2n)^2+(\b_1m+\b_2n)^2|^{s/2}}\\&=\frac{1}{|m|^s|(\a_1+\a_2\mu)^2+(\b_1+\b_2\mu)^2|^{s/2}}\end{align*}ここで $\mu:=\frac{n}{m}$ です。これと $(m^2+n^2)^{-s/2}$ を比較します。比をとると\begin{align*}\frac{\frac{1}{(m^2+n^2)^{s/2}}}{\frac{1}{|\O_{m,n}|^s}}&=\frac{\frac{1}{|m|^s(1+\mu^2)^{s/2}}}{\frac{1}{|m|^s|(\a_1+\a_2\mu)^2+(\b_1+\b_2\mu)^2|^{s/2}}}\\&=\left[\frac{(\a_1+\a_2\mu)^2+(\b_1+\b_2\mu)^2}{1+\mu^2}\right]^\frac{s}{2}\end{align*}となります。これを実数 $\mu$ の関数と見なして$$f(\mu)=\frac{(\a_1+\a_2\mu)^2+(\b_1+\b_2\mu)^2}{1+\mu^2}$$と書きましょう。$\a_1\b_2-\a_2\b_1\neq0$ ですので $f(\mu)>0$ です。微分すると$$f'(\mu)=-2\frac{(\a_1\a_2+\b_1\b_2)\mu^2+(\a_1^2+\b_1^2-\a_2^2-\b_2^2)\mu-\a_1\a_2-\b_1\b_2}{(1+\mu^2)^2}$$分子が2次関数となっていることから $f'(\mu)=0$ となる $\mu$ は2次方程式の判別式$$D=(\a_1^2+\b_1^2-\a_2^2-\b_2^2)^2+4(\a_1\a_2+\b_1\b_2)^2\ge0$$より異なる2実解または実数の重解をもちます。実数解の個数や $\a_1\a_2+\b_1\b_2$ の符号によって増減表は異なりますが、例えば2つの実数解のときは
| $\mu$ | $-\infty$ | $\mu_1$ | $\mu_2$ | $+\infty$ | |||
| $f'(\mu)$ | $+$ | $0$ | $-$ | $0$ | $+$ | ||
| $f(\mu)$ | $\a_2^2+\b_2^2$ | $\nearrow$ | 極値1 | $\searrow$ | 極値2 | $\nearrow$ | $\a_2^2+\b_2^2$ |
なる形になり、「極値2」が最小値となります。$f(\mu)>0$ でしたから $f(\mu)$ は正の最小値をとります。増減表の2行目を+-+としましたが、-+-もあり得ます。そちらも同様です。次に重解となるケースでは極値は1つになり、その極値がやはり正の最小値となるか、$\a_2^2+\b_2^2$ が下限となります。$\a_2^2+\b_2^2$ は必ず正ですから、結局はどのようなケースでも $f(\mu)$ には正の下限 $\d$ が存在して$$f(\mu)\ge\d>0$$
この $\d$ は $\o_1$ , $\o_2$ によって決まっており、$\mu$ には依りません。$\mu=n/m$ として元の話に立ち返ると$$\frac{\frac{1}{(m^2+n^2)^{s/2}}}{\frac{1}{|\O_{m,n}|^s}}\ge\d^{s/2}$$\begin{equation}\therefore\quad\sum_{m,n}'\frac{1}{|\O_{m,n}|^s}\le\frac{1}{\d^{s/2}}\sum_{m,n}'\frac{1}{(m^2+n^2)^{s/2}}\tag{3}\end{equation}となりますので(3)の右辺の収束性を調べることにします。これは正項級数ですので和をとる順を勝手に決めます。$m\ge0$ , $n\ge0$ のみの和について考えれば十分です。$m=n$ , $m>n$ , $m<n$ に分けて和をとった場合、$$\sum_{m,n\ge0}'\frac{1}{(m^2+n^2)^{s/2}}=\frac{1}{2^{s/2}}\sum_{m=1}^\infty\frac{1}{m^s}+\sum_{m=1}^\infty\sum_{n=0}^{m-1}\frac{1}{(m^2+n^2)^{s/2}}+\sum_{n=1}^\infty\sum_{m=0}^{n-1}\frac{1}{(m^2+n^2)^{s/2}}$$右辺第2項について(第3項も同様に)$$\sum_{m=1}^\infty\sum_{n=0}^{m-1}\frac{1}{(m^2+n^2)^{s/2}}\le\sum_{m=1}^\infty\frac{m}{(m^2)^{s/2}}=\sum_{m=1}^\infty\frac{1}{m^{s-1}}$$となることから $s>2$ なら収束します。よって(3)右辺は $s>2$ ならば収束します(十分条件。$s\le2$ での収束性は議論の余地あり)。したがって(3)より $s>2$ ならば $\sum_{}'|\O_{m,n}|^{-s}$ は収束します。以上から$$\sum_{m,n}'\left[\frac{1}{(z-\O_{m,n})^2}-\frac{1}{\O_{m,n}^{~2}}\right]$$は絶対一様収束します。
ペー関数の定義を再掲しましょう。\begin{equation}\wp(z):=\frac{1}{z^2}+\sum_{m,n}'\left[\frac{1}{(z-\O_{m,n})^2}-\frac{1}{\O_{m,n}^{~2}}\right]\tag{4}\end{equation}無限級数が絶対一様収束するので、和をとる順は好きに変えてもよく、$\wp(z)$ は2位の極 $\O_{m,n}$ を除いて解析的で項別微分が可能です。\begin{equation}\wp'(z)=-2\sum_{m,n}\frac{1}{(z-\O_{m,n})^3}\tag{5}\end{equation}(5)の和は $(m,n)=(0,0)$ を含んでいることに注意。$-z$ を代入すると\begin{equation}\wp'(-z)=2\sum_{m,n}\frac{1}{(z+\O_{m,n})^3}\tag{6}\end{equation}$\O_{m,n}=-\O_{-m,-n}$ であることと、$m,n$ に全整数を入れた時の$\O_{m,n}$ の集合と $\O_{-m,-n}$ の集合は同じです。和の順を変えていいことも併せて\begin{equation}\wp'(z)=-\wp'(-z)\tag{6'}\end{equation}つまりペー関数の導関数は奇関数です。
同様に(4)と\begin{equation}\wp(-z)=\frac{1}{z^2}+\sum_{m,n}'\left[\frac{1}{(z+\O_{m,n})^2}-\frac{1}{\O_{m,n}^{~2}}\right]\tag{7}\end{equation}により\begin{equation}\wp(z)=\wp(-z)\tag{8}\end{equation}つまりペー関数は偶関数です。
(5)より$$\wp'(z+\o_1)=-2\sum_{m,n}\frac{1}{(z-\O_{m-1,n})^3}$$$\O_{m-1,n}$ を $\O_{m,n}$ としても級数としては同じ値になりますので(和の順は好きに変えてよい)、$$\wp'(z+\o_1)=\wp'(z)$$積分して$$\wp(z+\o_1)=\wp(z)+C$$$z=-\o_1/2$ を代入すると$$\wp\left(\frac{\o_1}{2}\right)=\wp\left(-\frac{\o_1}{2}\right)+C$$(8)より $C=0$ 。$\o_2$ でも同様の手続きで\begin{equation}\wp(z+\o_1)=\wp(z+\o_2)=\wp(z)\tag{9}\end{equation}したがって $\wp(z)$ は二重周期性をもち、極のみを特異点としてもつ(有理型関数)ので楕円関数です。
(4)より $z=0$ で $\wp(z)$ は2位の極をもちますが、$\wp(z)-1/z^2$ は $z=0$ まわりにテイラー展開できます。偶関数であることも併せると\begin{align}\wp(z)-\frac{1}{z^2}&=\sum_{m,n}'\left[\frac{1}{(z-\O_{m,n})^2}-\frac{1}{\O_{m,n}^{~2}}\right]\\&=a_0+a_2z^2+a_4z^4+\cdots\tag{10}\end{align}$z=0$ とすると $a_0=0$ を得ます。\begin{align}\wp(z)-\frac{1}{z^2}&=\sum_{m,n}'\left[\frac{1}{(z-\O_{m,n})^2}-\frac{1}{\O_{m,n}^{~2}}\right]\\&=a_2z^2+a_4z^4+a_6z^6+\cdots\tag{11}\end{align}2回微分すると\begin{align}\wp''(z)-\frac{6}{z^4}&=6\sum_{m,n}'\frac{1}{(z-\O_{m,n})^4}\\&=2a_2+12a_4z^2+30a_6z^4+\cdots\tag{12}\end{align}$z=0$ とすると$$a_2=3\sum_{m,n}'\frac{1}{\O_{m,n}^{~4}}$$(12)をさらに2回微分すると$$a_4=5\sum_{m,n}'\frac{1}{\O_{m,n}^{~6}}$$を得ます。繰り返していけば
ペー関数は次のように展開できる。$$\wp(z)=\frac{1}{z^2}+\sum_{k=1}^\infty(2k+1)G_{2k+2}z^{2k}$$ただし$$G_{2k}:=\sum_{m,n}'\frac{1}{\O_{m,n}^{~2k}}=\sum_{m,n}'\frac{1}{(m\o_1+n\o_2)^{2k}}$$をアイゼンシュタイン級数という。
アイゼンシュタイン級数の主流の定義は若干これと異なりますが、定数倍の違いなので今は気にしません。一応展開式ができましたが、この級数の得体が全く知れません。定義から $\o_1,\o_2$ によって値が決まるのは分かりますが、ではどんな値なの、と。でも気にせず進めます。
※特殊なケースでアイゼンシュタイン級数の計算をしているのがこちら。
不変量(invariant)を次のように定義します。\begin{equation}g_2:=60G_4\;,\quad g_3:=140G_6\tag{13}\end{equation}何のためにこうするのかは今は気にしません。すると定理1の展開式を書き換えて\begin{equation}\wp(z)=\frac{1}{z^2}+\frac{g_2}{20}z^2+\frac{g_3}{28}z^4+O(z^6)\tag{14}\end{equation}これを微分したものは\begin{equation}\wp'(z)=-\frac{2}{z^3}+\frac{g_2}{10}z+\frac{g_3}{7}z^3+O(z^5)\tag{15}\end{equation}(14)を3乗したものは\begin{equation}\wp(z)^3=\frac{1}{z^6}+\frac{3g_2}{20}z^{-2}+\frac{3g_3}{28}+O(z^2)\tag{16}\end{equation}(15)を2乗したものは\begin{equation}\wp'(z)^2=\frac{4}{z^6}-\frac{2g_2}{5}z^{-2}-\frac{4g_3}{7}+O(z^2)\tag{17}\end{equation}(16)(17)から $z^{-6}$ を消去すると\begin{equation}\wp'(z)^2-4\wp(z)^3+g_2\frac{1}{z^2}+g_3=O(z^2)\tag{18}\end{equation}$\wp(z)=z^{-2}+O(z^2)$ より(18)は\begin{equation}\wp'(z)^2-4\wp(z)^3+g_2\wp(z)+g_3=O(z^2)\tag{19}\end{equation}と書き換えられます。$\wp(z)$ が楕円関数であるので(19)左辺全体は楕円関数。また(19)左辺は $z=\O_{m,n}$ で解析的でない可能性があるものの、右辺と比較するとそれらはすべて解析的な点であることが分かります。つまり(19)左辺は特異点をもたない楕円関数であり、すなわち定数です。$$\wp'(z)^2-4\wp(z)^3+g_2\wp(z)+g_3=\mathrm{const.}$$$z\to0$ とすれば(19)で $O(z^2)\to0$ ですから、この定数はゼロです。よって
ペー関数は次の式をみたす。$$\wp'(z)^2-4\wp(z)^3+g_2\wp(z)+g_3=0$$ただし $g_2,g_3$ は $\o_1,\o_2$ によって決まる定数で $g_2=60G_4$ , $g_3=140G_6$.
逆に、\begin{equation}\left(\frac{dy}{dz}\right)^2=4y^3-g_2y-g_3\tag{20}\end{equation}なる微分方程式が与えられたとしましょう。ここで与えられた $g_2,g_3$ から $g_2=60\sum'\O_{m,n}^{-4}$ , $g_3=140\sum'\O_{m,n}^{-6}$ をみたす $\o_1,\o_2$ が見つかったとします(詳細はここでは触れず、気にしない)。周期 $\o_1,\o_2$ をもつペー関数を使って $y=\wp(u)$ とおくと $\frac{dy}{dz}=\wp'(u)\frac{du}{dz}$ から$$\wp'(u)^2\left(\frac{du}{dz}\right)^2=4\wp(u)^3-g_2\wp(u)-g_3\overset{定理2}{=}\wp'(u)^2$$なので $u'=\pm 1$ となって、積分定数 $\a$ をもちいて $u=\pm z+\a$ となります。よって $y=\wp(\pm z+\a)$。$\wp(z)=\wp(-z)$ より $y=\wp(z+\a)$ として一般性を失いません。
微分方程式$$\left(\frac{dy}{dz}\right)^2=4y^3-g_2y-g_3$$の一般解は、$g_2,g_3$ に対応する周期 $\o_1,\o_2$ をもつペー関数を使って$$y(z)=\wp(z+\a)$$と書ける。
ただし $g_2,g_3$ には対応する二重周期 $\o_1,\o_2$ がなくてはなりません。例えば $g_2=g_3=0$ とした場合、微分方程式は簡単に解けて $y=\pm 2(z+C)^{-3}$ となりますが、これは楕円関数ではありません。ペー関数の話をするにあたって、例えば定理2の式からスタートする場合は $\o_1,\o_2$ よりも $g_2,g_3$ ありきのほうが有難いわけですが、そのあたりは気を付ける必要があります。詳細はいずれ書くかもしれません。
次回はペー関数の展開式について、もう少し詳しく見ていきます:
第5版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

複素解析の超定番本です。

複素解析(Amazon)
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。