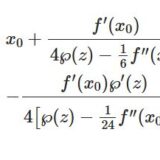前回は：
ワイエルシュトラスのペー関数７～シグマ関数：擬周期性をもつ整関数
本記事ではワイエルシュトラスのペー関数の基本的性質を前提知識としていますので
およびその続きをある程度ご覧になっておくといいと思います。
任意の定数でない楕円関数 $f(z)$ は\begin{equation}f(z)=\underbrace{\frac{f(z)+f(-z)}{2}}_{even}+\underbrace{\frac{f(z)-f(-z)}{2}}_{odd}\tag{1}\end{equation}のように偶関数と奇関数の和で書けます。さらに\begin{equation}f(z)=\underbrace{\frac{f(z)+f(-z)}{2}}_{even}+\underbrace{\frac{f(z)-f(-z)}{2\wp'(z)}}_{even}\;\wp'(z)\tag{2}\end{equation}のようにしておきます。つまり $f(z)$ は偶関数である楕円関数および $\wp'$ で表されることになります（$\wp'$ は奇関数）。
いま $f(z)$ を $\wp(z),\wp'(z)$ で表現することを目標とすると、(2)より任意の偶関数性をもつ楕円関数 $g(z)$ について論じればよいことになります。
なお $f(z)$ がそもそも偶関数なら(1)の変形は不要です。奇関数なら $\frac{f}{\wp'}\wp'$ とだけ変形すればよいです。
$g(z)$ の偶関数性より零点は$$z=\pm a_1,\;\pm a_2,\cdots,\;\pm a_n$$およびそれらと合同な点です。
極は$$z=\pm b_1,\;\pm b_2,\cdots,\;\pm b_n$$およびそれらと合同な点です。2位以上の極や零点がある場合はその位数分だけ登場させればよいです。
ここで$$F(z):=\frac{1}{g(z)}\prod_{k=1}^n\frac{\wp(z)-\wp(a_k)}{\wp(z)-\wp(b_k)}$$と定義すると $F(z)$ は楕円関数であり、極をもちません。というのも分母分子によって $g(z)$ の零点と極を打ち消すとともに、$\wp(z)$ 自身も極をもってしまうものの分母・分子に同じ数の $\wp(z)$ があることによって打ち消しあっているからです。ここで大事なのはとにかく $F(z)$ の極を無くすこと。それを意識すれば、$g(z)$ が $z=0$ に零点を持つような場合（上述の式そのままではおかしくなる）でも応用可能です。
極をもたない楕円関数は定数関数に限りますので $F(z)$ は定数より\begin{equation}g(z)=\mathrm{Const.}\prod_{k=1}^n\frac{\wp(z)-\wp(a_k)}{\wp(z)-\wp(b_k)}\tag{3}\end{equation}なので $g$ は $\wp$ の有理式になっています。
(2)と合わせると
定数でない任意の楕円関数 $f(z)$ は同一の周期をもったペー関数を用いて$$f(z)=R_1(\wp(z))+R_2(\wp(z))\wp'(z)$$と書ける。ただし $R_1,R_2$ は有理関数を表し、(2)(3)によって具体的に表式化される。
\begin{equation}\wp'(z)^2=4\wp(z)^3-g_2\wp(z)-g_3\tag{4}\end{equation}であったことを思い出しましょう。定理１に適用すると $f(z)$ は $\wp(z)$ によって代数的に表現されます（四則演算と累乗で表せるということ）。
定理１を使っていろいろな楕円関数を表現してみたのですが、時間があるときにまた加筆します。
同一周期の２つの楕円関数 $f(z),g(z)$ があるとします。定理１より$$\begin{cases}f(z) &=R_1(\wp)+R_2(\wp)\wp'\\g(z) &=R_3(\wp)+R_4(\wp)\wp'\end{cases}$$よって任意の楕円関数のペア(同一周期のもの)は代数的に結びついています。
そこから例えば $f(z)$ と $f'(z)$ は代数的に結びついていること、$f(z)$ と $f(z+\a)$ は代数的に結びついていることなどがいえます。
任意の定数でない楕円関数 $f(z)$ が $z=u_i$ に $r_i$ 位の極をもつとします。ただし $i=1,2,\cdots,n$ です。
$f(z)$ の主要部に着目します。$z=u_i$ でのローラン展開\begin{equation}f(z)=\frac{a_{i,r_i}}{(z-u_i)^{r_i}}+\frac{a_{i,r_i-1}}{(z-u_i)^{r_i-1}}+\cdots+\frac{a_{i,1}}{z-u_i}+O\left((z-u_i)^0\right)\tag{5}\end{equation}ワイエルシュトラスのゼータ関数 $\zeta(z)$ は $z\equiv 0$ に1位の極をもち、その留数は $1$ ですので\begin{equation}\zeta(z-u_i)=\frac{1}{z-u_i}+O\left((z-u_i)^0\right)\tag{6}\end{equation}(6)の正則部分は実際には3次の項からはじまるのですが、今は気にしません。
(5)の-1次の項と(6)をよく見ます。(5)から $a_{i,1}\zeta(z-u_i)$ を差し引くと(5)の-1次の項が主要部から消えます。つまり\begin{equation}f(z)-a_{i,1}\zeta(z-u_i)=\frac{a_{i,r_i}}{(z-u_i)^{r_i}}+\frac{a_{i,r_i-1}}{(z-u_i)^{r_i-1}}+\cdots+\frac{a_{i,2}}{(z-u_i)^2}+O\left((z-u_i)^0\right)\tag{7}\end{equation}次に(6)の微分\begin{equation}\zeta'(z-u_i)=\frac{-1}{(z-u_i)^2}+O\left((z-u_i)^0\right)\tag{8}\end{equation}と(7)を見比べると、先ほどと同様に(7)の-2次の項を主要部から消すことができます。つまり\begin{equation}f(z)-a_{i,1}\zeta(z-u_i)+a_{i,2}\zeta'(z-u_i)=\frac{a_{i,r_i}}{(z-u_i)^{r_i}}+\cdots+\frac{a_{i,3}}{(z-u_i)^3}+O\left((z-u_i)^0\right)\tag{9}\end{equation}次に(8)を微分して(9)から-3次の項を消す。これをくりかえして主要部を全部除きます。結果は\begin{equation}f(z)-\sum_{k=1}^{r_i}\frac{(-1)^{k-1}a_{i,k}}{(k-1)!}\zeta^{(k-1)}(z-u_i)=O\left((z-u_i)^0\right)\tag{10}\end{equation}(10)においては右辺が $z=u_i$ まわりで正則になっています。この操作を極 $u_1,u_2,\cdots,u_n$ すべてについて行います。すると\begin{equation}f(z)-\sum_{i=1}^n\sum_{k=1}^{r_i}\frac{(-1)^{k-1}a_{i,k}}{(k-1)!}\zeta^{(k-1)}(z-u_i):=F(z)\tag{11}\end{equation}なる $F(z)$ は極をもたないことになります。
さて $F(z)$ が楕円関数であるかを調べます（二重周期性を調べる）。というのも $\zeta$ の導関数はペー関数なので楕円関数であることは自明ですが、$\zeta$ 自身は楕円関数ではないからです。$f(z)$ は楕円関数と定義しましたから結局は$$F(z+\o_1)-F(z)=\sum_{i=1}^n a_{i,1}\left[\zeta(z+\o_1-u_i)-\zeta(z-u_i)\right]$$\begin{equation}\therefore\quad F(z+\o_1)-F(z)=\eta_1\sum_{i=1}^n a_{i,1}\tag{12}\end{equation}右辺の総和部分は、楕円関数 $f(z)$ の極の留数の総和であり、楕円関数一般の性質からゼロです。\begin{equation}\therefore\quad F(z+\o_1)=F(z)\tag{13}\end{equation}$\o_2$ についても同様なので $F(z)$ は二重周期性をもちますが、前述したように極をもちません。よって $F(z)$ は定数関数です。
以上より
任意の楕円関数 $f(z)$ は同一の周期をもったワイエルシュトラスのゼータ関数を用いて$$f(z)=A+\sum_{i=1}^n\sum_{k=1}^{r_i}\frac{(-1)^{k-1}a_{i,k}}{(k-1)!}\zeta^{(k-1)}(z-u_i)$$と書ける。ただし $A$ は定数。
$f$ の極だけしらべればよくて、零点の情報が要らないところが定理１と異なります。$\zeta^{(k-1)}(z-u_i)$ を明示的に表現するのが一般的に困難ではありますが。
$\wp(z)^2$ を定理２の形で表す。
$\wp$ は $z=0$ にのみ極をもつ。$\wp(z)=z^{-2}+O(z^2)$ より $\wp^2=z^{-4}+O(1)$ である。よって $\wp^2$ は $z=0$ に4位の極をもつ。よって定理２より$$\wp(z)^2=A+\sum_{k=1}^{4}\frac{(-1)^{k-1}a_{k}}{(k-1)!}\zeta^{(k-1)}(z)$$で $a_4=1$ , $a_3=a_2=a_1=0$ であるから$$\wp(z)^2=A-\frac{1}{6}\zeta^{(3)}(z)=A+\frac{1}{6}\wp''(z)$$とあらわせる。
実際、$$\wp(z)^2=\frac{g_2}{12}+\frac{1}{6}\wp''(z)$$であることがこちらで分かっている。
$f(z)$ を周期 $\o_1,\o_2$ の楕円関数とし、零点を$$z=a_1,a_2,\cdots,a_n$$
極を$$z=b_1,b_2,\cdots,b_n$$とします。こちらの定理10より$$a_1+a_2+\cdots+a_n\equiv b_1+b_2+\cdots+b_n\quad(\mathrm{mod}\;\o_1,\o_2)$$です。これら $2n$ 個の数のうちの１つを（あるいは複数を）合同な別の数に置き換えることによって\begin{equation}a_1+a_2+\cdots+a_n= b_1+b_2+\cdots+b_n\tag{14}\end{equation}とすることができます。
例えば $\wp'(z)$ は $z=0$ に3位の極をもつので$$b_1+b_2+b_3=0+0+0=0$$です。そして $\frac{\o_1}{2}$,$\frac{\o_2}{2}$,$\frac{\o_1+\o_2}{2}$ に1位の零点をもちますので$$a_1+a_2+a_3=\frac{\o_1}{2}+\frac{\o_2}{2}+\frac{\o_1+\o_2}{2}=\o_1+\o_2$$この時点で(14)は不成立ですが $a_3=\frac{\o_1+\o_2}{2}$ としているところを、合同な別の点 $-\frac{\o_1+\o_2}{2}$ に置き換えると$$a_1+a_2+a_3=0$$となり(14)が満たされます。
さて、$f(z)$ と同一周期(正確には擬周期)のシグマ関数をもちいて\begin{equation}\prod_{k=1}^n\frac{\sigma(z-a_k)}{\sigma(z-b_k)}\tag{15}\end{equation}なる関数を定義します。$\sigma(z)$ は $z\equiv0$ のみに1位の零点をもつ整関数でしたから、(15)は $f(z)$ と同じく $a_k$ に1位の零点、$b_k$ に1位の極をもちます。
さらに(15)の周期性を調べると\begin{align}\prod_{k=1}^n\frac{\sigma(z+\o_1-a_k)}{\sigma(z+\o_1-b_k)} &=\prod_{k=1}^n\frac{-\exp\left(\eta_1(z+\frac{\o_1}{2}-a_k)\right)\sigma(z-a_k)}{-\exp\left(\eta_1(z+\frac{\o_1}{2}-b_k)\right)\sigma(z-b_k)}\\ &=\prod_{k=1}^n\frac{e^{-\eta_1 a_k}\sigma(z-a_k)}{e^{-\eta_1 b_k}\sigma(z-b_k)}\\&=e^{-\eta_1(a_1+\cdots+a_n-b_1-\cdots b_n)}\prod_{k=1}^n\frac{\sigma(z-a_k)}{\sigma(z-b_k)}\\&=\prod_{k=1}^n\frac{\sigma(z-a_k)}{\sigma(z-b_k)}\end{align}最後は(14)を使いました。よって(15)は二重周期性をもつので楕円関数です。
ということは $f$ と(15)の比$$\frac{f(z)}{\prod_{k=1}^n\frac{\sigma(z-a_k)}{\sigma(z-b_k)}}$$が零点も極も持たない楕円関数ということになり、すなわち定数関数です。以上より、
任意の楕円関数 $f(z)$ は同一の周期をもったワイエルシュトラスのシグマ関数を用いて$$f(z)=A\prod_{k=1}^n\frac{\sigma(z-a_k)}{\sigma(z-b_k)}$$と書ける。ただし $A$ は定数。
極と零点が楕円関数の形を決めるといって過言ではないでしょう。
定理３によって $\wp(z)$ をシグマ関数で表現しようとしても零点が分からないため、不満が残ります。そこで下の系４のようなものを考えましょう。
$$\wp(z)-\wp(y)=-\frac{\sigma(z+y)\sigma(z-y)}{\sigma(z)^2\sigma(y)^2}$$
$y$ は周期でないとする。左辺を $z$ の関数とみると $z=0$ に2位の極を、$z=\pm y$ に1位の零点をもつ。$$\therefore\quad \wp(z)-\wp(y)=A(y)\frac{\sigma(z+y)\sigma(z-y)}{\sigma(z)^2}$$$\wp(z)=z^{-2}+O(z^2)$ より$$\wp(z)-\wp(y)=\frac{1}{z^2}+O(1)$$一方、前回の定理３aより$$\sigma(z+y)=\sigma(y)+O(z)\;,\sigma(z-y)=-\sigma(y)+O(z)$$$$\sigma(z)^2=z^2\left(1+O(z)\right)$$これらより $z\to 0$ の極限で$$A(y)=-\frac{1}{\sigma(y)^2}$$と求まる。
系４を $z,y$ で微分します。面倒ですが試してみるといい感じでコツがつかめ、ひとめで導関数が分かるようになります（ガンマ関数とかベータ関数の微分に似ている）。\begin{align}\wp'(z)&=\left(\wp(z)-\wp(y)\right)\left(\zeta(z+y)+\zeta(z-y)-2\zeta(z)\right)\\-\wp'(y)&=\left(\wp(z)-\wp(y)\right)\left(\zeta(z+y)-\zeta(z-y)-2\zeta(y)\right)\end{align}辺々足すと
$$\frac{1}{2}\frac{\wp'(z)-\wp'(y)}{\wp(z)-\wp(y)}=\zeta(z+y)-\zeta(z)-\zeta(y)$$
以前求めた擬加法定理と同じ結果です。
もう１つの例を見ましょう。
$$\wp'(z)=\frac{2\sigma(z-\frac{\o_1}{2})\sigma(z-\frac{\o_2}{2})\sigma(z-\frac{\o_3}{2})}{\sigma(z)^3\sigma(\frac{\o_1}{2})\sigma(\frac{\o_2}{2})\sigma(\frac{\o_3}{2})}$$ただし $\o_3=-\o_1-\o_2$ .
$\wp'$ は $z=0$ に3位の極を、$z=\frac{\o_1}{2}$,$\frac{\o_2}{2}$,$\frac{\o_3}{2}$ に1位の零点をもつ。$$\wp'(z)=A\frac{\sigma(z-\frac{\o_1}{2})\sigma(z-\frac{\o_2}{2})\sigma(z-\frac{\o_3}{2})}{\sigma(z)^3}$$両辺の $z=0$ まわりをみると\begin{align}\wp'(z) &=-\frac{2}{z^3}+O(z)\\\sigma(z)^3&=z^3\left(1+O(z)\right)\\\sigma\left(z-\frac{\o_r}{2}\right) &=-\frac{\o_r}{2}+O(z)\end{align}これらを使って $z\to 0$ の極限を調べると $A$ が定まる。
なお系６の分子についてはこちらの公式７によってちょっとだけ違う形に書くことができます。
第５版です。いわずと知れた名著。楕円関数にかなりのページを割いています。
次回は準備中。
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。