単発としても読めますが、シリーズを通して読むとベターです。前回の記事は:
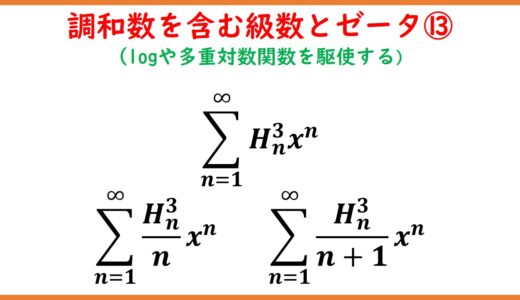
調和数を含んだ級数(Euler-sum)とゼータ関数 part11
類似シリーズ:
多重対数関数の基礎知識が必要です:
$n=0,1,2,\cdots$ に対して調和数 $H_n$ と奇調和数 $O_n$ および交代調和数 $h_n$ を次のように定義する。$$H_n=1+\frac{1}{2}+\cdots+\frac{1}{n}\quad,\quad H_0=0$$$$O_n=1+\frac{1}{3}+\cdots+\frac{1}{2n-1}\quad,\quad O_0=0$$$$h_n=1-\frac{1}{2}+\cdots+\frac{(-1)^{n-1}}{n}\quad,\quad h_0=0$$このとき級数と関数の等式として以下が証明できる。\begin{eqnarray*}\sum_{n=1}^\infty h_n x^n &=& \frac{\ln(1+x)}{1-x}\\ \sum_{n=1}^\infty \frac{h_n}{n} x^n &=& \Li_2\left(\frac{1-x}{2}\right)-\Li_2(-x)-\ln2\ln(1-x)-\frac{\pi^2}{12}+\frac{\ln^22}{2} \\\sum_{n=1}^\infty \frac{h_{2n-1}}{n} x^{2n} &=& -\ln(1+x)\ln(1-x) \\\sum_{n=1}^\infty \frac{h_{2n}}{n} x^{2n} &=& -\ln(1+x)\ln(1-x)-\frac{1}{2}\Li_2(x^2)\\ \sum_{n=1}^\infty \frac{h_{2n-1}}{2n+1} x^{2n-1} &=& \frac{1}{x^2}\Biggl[\Li_2\left(\frac{1-x}{2}\right)+\left(\frac{1}{2}-\ln2\right)\ln(1-x)\\&&\quad\quad-\frac{\ln(1+x)}{2}+\frac{\ln^22}{2}-\frac{\pi^2}{12}+\frac{\ln(1+x)\ln(1-x)}{2}\Biggr]\\&&+\frac{\mathrm{arctanh}x-\ln(1+x)+1}{x} \\ \sum_{n=1}^\infty \frac{h_{2n-1}}{(2n+1)^2} &=& -\frac{21}{16}\zeta(3)+\frac{\pi^2}{4}\ln2-\frac{\pi^2}{8}+2-\ln2\end{eqnarray*}また系の積分として次を得る。$$\int_0^1\ln u\ln(1+u)\ln(1-u)du=\frac{21}{8}\zeta(3)-\frac{\pi^2}{2}\ln2+\frac{5}{12}\pi^2-\ln^22+4\ln2-6$$
本シリーズでは初めて $h_n$ を扱います。$H_n$ , $O_n$ で得た知見と $h_{2n-1}=O_n-\frac{1}{2}H_{n-1}$ あるいは $h_{2n-1}=H_{2n}-H_n+\frac{1}{2n}$ を組み合わせて考えることもできますが、今回は 直接 $h_n$ を計算していきます。進め方は過去記事で $H_n$ や $O_n$ を扱った時と似ていますので、単発でも読めますが、本シリーズの初回から読んでいただくと理解が深まります。
過去記事でやったことを生かします。$\ln(1+x)=-x+\frac{x^2}{2}-\frac{x^3}{3}+\cdots$ , $(1-x)^{-1}=1+x+x^2+\cdots$ の積をとって展開し、昇べきにならべると次の母関数表示(Generating function)を得ます。Cauchy's productの公式をそのまま当てはめてOK。
\begin{equation}\sum_{n=1}^\infty h_n x^n = \frac{\ln(1+x)}{1-x}\tag{1}\end{equation}
収束する範囲で $x$ に値を代入すればさまざまな級数値を得ることができます。
(1)をとっかかりとして進めます。$x$ で割り、積分します。$$\sum_{n=1}^\infty \frac{h_n}{n} x^n=\int \frac{\ln(1+x)}{x(1-x)}dx$$右辺の積分は困難ですが、部分分数分解および $\Li_2(\frac{1-x}{2})$ の微分をしてみることで見通しが立ちます。$$\int \frac{\ln(1+x)}{x(1-x)}dx=\Li_2\left(\frac{1-x}{2}\right)-\Li_2(-x)-\ln2\ln(1-x)+C$$$x=0$ での値を考えることで $C$ が求まります。すなわち
\begin{equation}\sum_{n=1}^\infty \frac{h_n}{n} x^n = \Li_2\left(\frac{1-x}{2}\right)-\Li_2(-x)-\ln2\ln(1-x)-\frac{\pi^2}{12}+\frac{\ln^22}{2}\tag{2}\end{equation}
たとえば $x=-1$ とすると\begin{equation}\sum_{n=1}^\infty \frac{(-1)^nh_n}{n} = -\frac{\pi^2}{12}-\frac{\ln^22}{2}\tag{3}\end{equation}
こちらで導出した式として\begin{align}\sum_{n=0}^\infty\frac{h_n}{n^k}&=k\left(1-\frac{1}{2^k}-\frac{k}{2}\right)\zeta(k+1)\\&\quad+2\left(1-\frac{1}{2^{k}}\right)\zeta(k)\ln2\\&\quad+\frac{1}{2}\sum_{r=2}^{k-1}\eta(r)\eta(k-r+1)\end{align}があります。
$\ln(1+x)$ と $\ln(1-x)$ のCauchy's productを考えることで\begin{eqnarray*}\ln(1+x)\ln(1-x) &=& \left(\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n}x^n\right)\left(-\sum_{n=1}^\infty\frac{1}{n}x^n\right)\\ &=& -x^2\sum_{n=0}^\infty\sum_{k=0}^n\frac{(-1)^k}{k+1}\frac{1}{n-k+1}x^n \\&=& \sum_{n=2}^\infty\sum_{k=1}^{n-1}\frac{(-1)^k}{n}\left(\frac{1}{k}+\frac{1}{n-k}\right)x^n \\&=& \sum_{n=2}^\infty\frac{x^n}{n}\sum_{k=1}^{n-1}(-1)^k\left(\frac{1}{k}+\frac{1}{n-k}\right)\\&=& \sum_{n=2}^\infty\frac{x^n}{n}(-h_{n-1}+(-1)^{n-1}h_{n-1}) \\&=&-\sum_{n=1}^\infty\frac{x^{2n}}{2n}2h_{2n-1}\end{eqnarray*}したがって
\begin{equation}\sum_{n=1}^\infty \frac{h_{2n-1}}{n} x^{2n} = -\ln(1+x)\ln(1-x)\tag{4}\end{equation}
新たな級数公式を得るために「添え字をずらす」方法を紹介します(簡単)。本シリーズ過去記事でも多用しています。例えば(4)の左辺にある $h_{2n-1}$ を $h_{2n}$ とした級数が欲しければ、$h_n$ の定義式より $h_{2n}=h_{2n-1}-\frac{1}{2n}$ となりますので\begin{eqnarray*}\sum_{n=1}^\infty \frac{h_{2n}}{n} x^{2n} &=& \sum_{n=1}^\infty \frac{h_{2n-1}-\frac{1}{2n}}{n} x^{2n} \\&=& \sum_{n=1}^\infty \frac{h_{2n-1}}{n} x^{2n}-\frac{1}{2}\sum_{n=1}^\infty \frac{x^{2n}}{n^2}\\&=&-\ln(1+x)\ln(1-x)-\frac{1}{2}\Li_2(x^2)\quad(\because(4))\end{eqnarray*}よって
\begin{equation}\sum_{n=1}^\infty \frac{h_{2n}}{n} x^{2n} = -\ln(1+x)\ln(1-x)-\frac{1}{2}\Li_2(x^2)\tag{5}\end{equation}
練習として次の式を示しましょう。
\begin{eqnarray}\sum_{n=1}^\infty \frac{h_{2n-1}}{2n+1} x^{2n-1} &=& \frac{1}{x^2}\Biggl[\Li_2\left(\frac{1-x}{2}\right)+\left(\frac{1}{2}-\ln2\right)\ln(1-x)\\&&\quad\quad-\frac{\ln(1+x)}{2}+\frac{\ln^22}{2}-\frac{\pi^2}{12}+\frac{\ln(1+x)\ln(1-x)}{2}\Biggr]\\&&+\frac{\mathrm{arctanh}x-\ln(1+x)+1}{x}\tag{6}\end{eqnarray}
左辺の級数を書き下してみると、次の等式を確認できます。$$\sum_{n=1}^\infty \frac{h_{2n-1}}{2n+1} x^{2n-1}=\sum_{n=1}^\infty \frac{h_n}{n+2} x^n-\sum_{n=1}^\infty \frac{h_{2n}}{2n+2} x^{2n}$$右辺を変形します。$$=\sum_{n=1}^\infty \frac{h_{n+2}-\frac{(-1)^n}{n+1}-\frac{(-1)^{n+1}}{n+2}}{n+2} x^n-\frac{1}{2}\sum_{n=1}^\infty \frac{h_{2n+1}-\frac{1}{2n+1}}{n+1} x^{2n}$$よって\begin{eqnarray}\sum_{n=1}^\infty \frac{h_{2n-1}}{2n+1} x^{2n-1} &=& \frac{1}{x^2}\sum_{n=3}^\infty \frac{h_n}{n}x^n-\sum_{n=1}^\infty \frac{(-1)^nx^n}{(n+1)(n+2)}\\&&+\sum_{n=1}^\infty\frac{(-1)^nx^n}{(n+2)^2}-\frac{1}{2}\sum_{n=1}^\infty\frac{h_{2n+1}}{n+1}x^{2n}\\&&+\frac{1}{2}\sum_{n=1}^\infty\frac{x^{2n}}{(n+1)(2n+1)} \\&=& \frac{1}{x^2}\sum_{n=3}^\infty \frac{h_n}{n}x^n-\sum_{n=1}^\infty\frac{(-1)^nx^n}{n+1}+\sum_{n=1}^\infty\frac{(-1)^nx^n}{n+2}\\&&+\sum_{n=1}^\infty\frac{(-1)^nx^n}{(n+2)^2}-\frac{1}{2}\sum_{n=1}^\infty\frac{h_{2n+1}}{n+1}x^{2n}\\&&+\frac{1}{2}\sum_{n=1}^\infty\frac{x^{2n}}{(n+1)(2n+1)} \\&=& \frac{1}{x^2}\sum_{n=3}^\infty \frac{h_n}{n}x^n-\frac{1}{x}\sum_{n=2}^\infty\frac{(-1)^{n-1}x^n}{n}-\frac{1}{x^2}\sum_{n=3}^\infty\frac{(-1)^{n-1}x^n}{n}\\&&+\frac{1}{x^2}\sum_{n=3}^\infty\frac{(-1)^nx^n}{n^2}-\frac{1}{2x^2}\sum_{n=2}^\infty\frac{h_{2n-1}}{n}x^{2n}\\&&+\frac{1}{x}\sum_{n=1}^\infty\frac{x^{2n+1}}{2n+1}-\frac{1}{2x^2}\sum_{n=2}^\infty\frac{x^{2n}}{n}\end{eqnarray}第1項には(2)、第2,3項には $\ln(1+x)$ の展開式、第7項には $\ln(1-x^2)$ の展開式を使います。第4項は $\Li_2$ の級数表示を使います。第5項には(4)式を、第6項は $\mathrm{arctanh}$ の級数表示です。和それぞれ $n$ の下端が異なることに注意し、適宜、和に入らない項を引き算する必要があります。計算を完了させると
\begin{eqnarray}\sum_{n=1}^\infty \frac{h_{2n-1}}{2n+1} x^{2n-1} &=& \frac{1}{x^2}\Biggl[\Li_2\left(\frac{1-x}{2}\right)+\left(\frac{1}{2}-\ln2\right)\ln(1-x)\\&&\quad\quad-\frac{\ln(1+x)}{2}+\frac{\ln^22}{2}-\frac{\pi^2}{12}+\frac{\ln(1+x)\ln(1-x)}{2}\Biggr]\\&&+\frac{\mathrm{arctanh}x-\ln(1+x)+1}{x}\tag{7}\end{eqnarray}
(7)に $x$ をかけて $0$ から $1$ まで積分すると\begin{eqnarray*}\sum_{n=1}^\infty \frac{h_{2n-1}}{(2n+1)^2} &=& \int_0^1\Biggl[\frac{1}{x}\Biggl\{\Li_2\left(\frac{1-x}{2}\right)+\left(\frac{1}{2}-\ln2\right)\ln(1-x)\\&&\quad\quad\quad-\frac{\ln(1+x)}{2}+\frac{\ln^22}{2}-\frac{\pi^2}{12}+\frac{\ln(1+x)\ln(1-x)}{2}\Biggr\}\\&&\quad+\mathrm{arctanh}x-\ln(1+x)+1\Biggr]dx\end{eqnarray*}最大の難関は第1項なのですが、Wolframが不定積分を計算してくれます(すごい長い式になるのでここでは省略)。この項だけでは発散してしまうので積分下端を $\epsilon\ll1$ とすると$$\int_\epsilon^1\frac{\Li_2(\frac{1-x}{2})}{x}dx=-\zeta(3)+\Li_2\left(\frac{1}{2}\right)\ln2+\frac{\ln^32}{2}-\Li_2\left(\frac{1}{2}\right)\ln\epsilon$$次の第2項は $\Li_2$ の定義そのものです。すなわち$$\int_0^1\frac{\ln(1-x)}{x}dx=-\Li_2(1)=-\zeta(2)$$第3項も同様に$$\int_0^1\frac{\ln(1+x)}{x}dx=\int_0^{-1}\frac{\ln(1-x)}{x}dx=-\Li_2(-1)=\frac{\zeta(2)}{2}$$残りで難しいのは\begin{eqnarray*}\int_0^1\frac{\ln(1+x)\ln(1-x)}{x}dx &=& -\sum_{n=1}^\infty \frac{h_{2n-1}}{n} \int_0^1x^{2n-1}dx\quad(\because(4)) \\&=& -\frac{1}{2}\sum_{n=1}^\infty \frac{h_{2n-1}}{n^2}\\&=&-\frac{1}{2}\sum_{n=1}^\infty \frac{O_n-\frac{1}{2}H_{n-1}}{n^2}\\&=&\frac{1}{4}\sum_{n=1}^\infty \frac{H_{n-1}}{n^2}-\frac{1}{2}\sum_{n=1}^\infty \frac{O_n}{n^2}\\&=&\frac{1}{4}\zeta(3)-\frac{7}{8}\zeta(3)\\&=&-\frac{5}{8}\zeta(3)\end{eqnarray*}最後の変形はこことここと参照。あとはすべて初等的です。$1/x$ の項の積分は$$\left(\frac{\ln^22}{2}-\frac{\pi^2}{12}\right)\int_\epsilon^1\frac{dx}{x}=\Li_2\left(\frac{1}{2}\right)\ln\epsilon$$より先ほどの $\ln\epsilon$ と相殺します。結局
\begin{equation} \sum_{n=1}^\infty \frac{h_{2n-1}}{(2n+1)^2} = -\frac{21}{16}\zeta(3)+\frac{\pi^2}{4}\ln2-\frac{\pi^2}{8}+2-\ln2\tag{8}\end{equation}
ここまでの事実は、多くの積分計算につながります。例として次の系を示しましょう。
\begin{equation}\int_0^1\ln u\ln(1+u)\ln(1-u)du=\frac{21}{8}\zeta(3)-\frac{\pi^2}{2}\ln2+\frac{5}{12}\pi^2-\ln^22+4\ln2-6\tag{9}\end{equation}
(4)を用いて級数の形にし、項別積分を行います。$$\int_0^1\ln u\ln(1+u)\ln(1-u)du=\sum_{n=1}^\infty \left(\frac{h_{2n-1}}{n}-2\frac{h_{2n-1}}{2n+1}-2\frac{h_{2n-1}}{(2n+1)^2}\right) $$あとは(4)(6)(7)を使えばOK(積分の上端は $1-\epsilon$ として計算する)。
次はこちら
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。