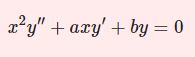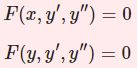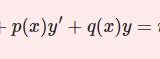オイラー・コーシーの方程式は斉次線型微分方程式の一種であり、すべての項が $x$ について同じ「べき」となっているものである。単純に見えて意外にも多様な解を得られるので面白い。ここでは2階微分方程式の1項目として扱っているが、より高階でも応用可能である。
1,2階微分方程式の基本については以下の記事を参照ください。
【D1】１階線型微分方程式の解法
【D5】斉次2階線型微分方程式
\begin{equation}x^2y^{\prime\prime}+axy'+by=0\tag{1}\end{equation}
これはオイラー・コーシーの方程式とよばれ、斉次2階線型微分方程式の一種です。左辺に3つの項がありますが $3$ 項とも $x$ について同じ「べき」となっています（微分は $x$ の次数を１つ下げるため）。そこで $y=x^n $ を試行解として(1)に代入すると、$$n(n-1)x^n+anx^n+bx^n=0$$
よって $n$ の方程式$$n^2+(a-1)n+b=0$$から得られる $n$ を用いれば $y=x^n$ が特殊解となります。$n$ についての2次方程式なので2つの解を得て、対応する2つの特殊解 $y_1=x^{n_1}$ , $y_2=x^{n_2}$ が得られるわけです。それらを線型結合すれば一般解ですね。
しかし $n$ が重解の場合はどうなるのでしょうか？
重解の場合はまずその特殊解 $y_1$ を得ます。１つの特殊解 $y_1$ が分かっている場合、もう１つの特殊解は $y_2=y_1u(x)$ と表されます。これを試行解として $u(x)$ を求めればいいです。
こういう解法については過去記事
【D5】斉次2階線型微分方程式
の前半（階数低減法）を参照ください。
今の段階では解は $x^n$ の形しか現れないように思えますが、意外に多様な解が得られて面白いです。下記の例題たちを見てください。
$x^2y^{\prime\prime}-\displaystyle\frac{5}{2}xy'-2y=0 $ を解け．
試行解 $y=x^n$ を代入すると$$n(n-1)-\frac{5}{2}n-2=0$$これを整理して$$n^2-\frac{7}{2}n-2=0 \;\Longrightarrow\; n=-\frac{1}{2}\; ,\; 4$$よって特殊解は$$x^{-\frac{1}{2}}\;,\;x^4$$特殊解が２つ見つかったので一般解はこの線型結合です。$$\therefore\quad y=\frac{c_1}{\sqrt{x}}+c_2x^4$$
$x^2y^{\prime\prime}-3xy'+4y=0 $ を解け．
$y=x^n$ を代入すると$$n(n-1)-3n+4=0$$これを解くと $n=2$ の重解を得ます。これにより特殊解は $x^2$ ですがもう１つの特殊解を探す必要があります。
１つの特殊解 $y_1$ が分かっている場合、もう１つの特殊解は $y_2=y_1u(x)$ と表されます。これを試行解として $u(x)$ を求めます。すなわち\begin{eqnarray*}y_2&=&x^2u\\ y'_2&=&2xu+x^2u'\\y^{\prime\prime}_2&=& 2u+4xu'+x^2u^{\prime\prime}\end{eqnarray*}をもとの微分方程式に代入すると$$x^2(2u+4xu'+x^2u^{\prime\prime})-3x( 2xu+x^2u' )+4 x^2u =0$$整理して$$u''=-\frac{1}{x}u'$$となります。これは $u'(x)$ についての1階微分方程式です。$u'$ と $x$ を変数分離して積分することにより\begin{equation}u'=\frac{c_1}{x}\tag{2}\end{equation}さらに積分して$$u=c_1\log x+c$$よって2つ目の特殊解は $y_2=x^2(c_1\log x+c_2)$ です。以上から一般解は$$y=c_1x^2\log x+c_2x^2$$となります。
式(2)を得る積分では本来 $z,x$ に絶対値がつきますが、定数 $c_1$ は正負の値をとりうるので不要となります。
$x^2y^{\prime\prime}-xy'+2y=0 $ を解け．
$y=x^n $ を代入すると$$n^2-2n+2=0$$となって $n=1+i\;,\;1-i$ なる虚数解を得ます。よって一般解は\begin{eqnarray*}y &=& Ax^{1+i}+Bx^{1-i}\\ &=& x(Ax^i+Bx^{-i})\\ &=& x(Ae^{i\log x}+Be^{-i\log x})\\ &=& x[A(\cos\log x+i\sin\log x)+B(\cos\log x-i\sin\log x)]\\ &=& x[(A+B)\cos\log x+i(A-B)\sin\log x]\\ &=& x(c_1\cos\log x +c_2\sin\log x)\end{eqnarray*}
半径 $r_1$ , $r_2$ の金属製の同心球殻がある($r_1<r_2$)．小さい方の球殻は電位 $V_1$ に帯電しており，大きい方の球殻は接地されている．このとき２つ球殻の間にある空間の電位を考えたい．球殻の中心を原点として，原点からの距離 $r\in[r_1,r_2]$ の電位 $\phi (r)$ を求めよ．
手順によってはオイラー・コーシー方程式に帰着しませんが・・・。電荷のない空間におけるマクスウェル方程式$$\nabla \cdot\boldsymbol{E}=0$$および電位と電場の関係$$\boldsymbol{E}=-\nabla\phi$$を組み合わせると\begin{equation}\Delta\phi=0\tag{3}\end{equation}これを球座標系に書き換えるとき、電位は $r$ のみに依存しますから角度成分の偏微分は省いて$$\Delta\phi=\frac{1}{r^2}\frac{d}{dr}\left(r^2 \frac{d\phi}{dr} \right)$$となりますので(3)は$$ \frac{d}{dr}\left(r^2 \frac{d\phi}{dr} \right)=0$$計算を進めて\begin{equation}r^2\phi^{\prime\prime}+2r\phi'=0\tag{4}\end{equation}これはオイラー・コーシー型になっています。もっとも $\phi$ の項がないので1階方程式の要領で解けるのですが、本記事の実践として扱います。
$\phi=r^n$ を式(4)に代入すると $n=0,1$ を得ますので$$\phi(r)=c_1+\frac{c_2}{r}$$となります。ここで与えられた条件 $\phi(r_1)=V_1$ , $\phi(r_2)=0$ を用いれば$$c_1=-\frac{c_2}{r_2}$$$$c_2=\frac{r_1r_2}{r_2-r_1}V_1$$と決定され$$\therefore\quad\phi(r)=\frac{r_1r_2}{r_2-r_1}V_1\left(\frac{1}{r}-\frac{1}{r_2}\right)$$
オイラー・コーシーの方程式$$ x^2y^{\prime\prime}+axy'+by=0 $$に$x=e^t$ なる変換をほどこすと$$\frac{dy}{dx}=\frac{1}{x}\frac{dy}{dt}$$$$\frac{d^2y}{dx^2}=\frac{1}{x^2}\left(\frac{d^2y}{dt^2}-\frac{dy}{dt}\right)$$となるので$$ \frac{d^2y}{dt^2} +(a-1)\frac{dy}{dt}+by=0$$よって定数係数の方程式に帰着させることができます。
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
常微分シリーズ過去記事
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
