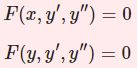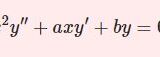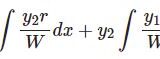非斉次２階線型微分方程式の解法の１つ「試行解による方法」を解説する。非斉次の場合は、斉次方程式の一般解にもう１つ特殊解と足し合わせることで解が得られる。ではその「もう１つの特殊解」とやらはどのようにして得られるのだろう？その１つが本記事のテーマである。
前提知識となる過去記事はこちら
【D5】斉次2階線型微分方程式
$$y^{\prime\prime}+p(x)y'+q(x)y=r(x)$$
この場合は斉次方程式 $r(x)=0$ 仮定した場合の一般解を求め、それにもう１つの特殊解を足し合わせることで解くことができます。斉次方程式の一般解の求め方は過去にパターン別で説明しましたので過去記事を参照ください。
つまり非斉次方程式のポイントは「もう１つの特殊解」をどう見つけるのかということになります。その方法の1つが試行解による方法であり、本記事のテーマとなります。
$y^{\prime\prime}+3y'+2y=4x^2$ を解け．
斉次方程式 $y^{\prime\prime}+3y'+2y=0$ の場合、定数係数の方程式ですので試行解 $y=e^{\lambda x}$ を代入して計算を進めると解は$$y_0=c_1e^{-x}+c_2e^{-2x}$$と求まります。
非斉次の話に戻ります。ここでもう１つの試行解 $y_p=ax^2+bx+c$ を方程式に代入すると$$2a+3(2ax+b)+2(ax^2+bx+c)=4x^2$$これを整理して $a,b,c$ を求めた結果$$y_p=2x^2-6x+7$$という特殊解を得ます。なぜこのような試行解を選んだかというと、与えられた微分方程式の右辺が2次式であるため、左辺も2次式だと考えられるためです。最終的な答えは、斉次の一般解 $y_0$ とこの特殊解 $y_p$ を足し合わせて$$y=c_1e^{-x}+c_2e^{-2x}+2x^2-6x+7$$となります。実際に代入して確かめてみましょう。
$y^{\prime\prime}+6y'+9y=50e^{-x}\cos x$ を解け．
斉次方程式 $ y^{\prime\prime}+6y'+9y =0$ の解は$$y_0=e^{-3x}(c_1x+c_2)$$です。
微分方程式の右辺が $e^{-x}\cos x$ となっているので、左辺にも似たようなものが入るでしょうが、$e^{-x}$ は微分しても形を変えず $\cos$ は微分によって $\sin$ に変化することから、非斉次の特殊解 $y_p=e^{-x}(a\cos x+ b\sin x)$ と予想します。これを試行解としてもとの方程式に代入すると$$(-4a+3b)\sin x+(3a+4b)\cos x=50\cos x$$を得て$a=6,b=8$ と求まります。よって$$y_p=e^{-x}(6\cos x+ 8\sin x)$$求める一般解は$$y=e^{-3x}(c_1x+c_2)+2e^{-x}(3\cos x+ 4\sin x)$$
$y^{\prime\prime}-y'-\displaystyle\frac{3}{4}y=21\sinh 2x$ を解け．
斉次の解は$$y_0=c_1e^{\frac{3}{2}x}+c_2e^{-\frac{1}{2}x}$$
微分方程式の右辺が $\sinh 2x$ となっているので左辺にも同じものが入るでしょうが、$\sinh$ は微分によって $\cosh$ に変化することから、それも含めた非斉次の特殊解 $y_p=a\sinh 2x+ b\cosh 2x$ と予想します。これをもとの方程式に代入し$$(\frac{13}{4}a-2b)\sinh 2x+(-2a+\frac{13}{4}b)\cosh 2x=21\sinh 2x$$これより $a=52/5,b=32/5$ と求まります。よって$$y_p=\frac{42e^{2x}-10e^{-2x}}{5}$$ここで $\cosh , \sinh$ と $e^x,e^{-x}$ の関係を用いています。
求める一般解は$$y=c_1e^{\frac{3}{2}x}+c_2e^{-\frac{1}{2}x}+\frac{42e^{2x}-10e^{-2x}}{5}$$
$y^{\prime\prime}-3y'+2y=2e^x$ を解け．
斉次解は $y_0=c_1e^x+c_2e^{2x}$ です。
これまでのパターンで行くと試行解を $ae^x$ としたいのですが、この解は斉次解に含まれているのでダメです。この場合は試行解を $axe^x$ と修正して方程式に代入すると $a=-2$ となります。したがって求める解は$$y= c_1e^x+c_2e^{2x} -2xe^x$$
$y^{\prime\prime}-2y'+y=e^x$ を解け．
斉次解は $y_0=c_1e^x+c_2xe^x$ です。
$e^x$ は斉次解に含めれているので、例題４と同じように試行解を $axe^x$ とするとこれもやはり斉次解に含まれています。この場合は試行解を $ax^2e^x$ と修正して方程式に代入すると $a=-1/2$ となります。したがって求める解は$$y= c_1e^x+c_2xe^x -\frac{1}{2}x^2e^x$$
以上の例題を通じて共通するのは、まず斉次解を求めることです。このとき２つの定数が含まれます。そして2階微分方程式の定数は２つですから、このあと求める非斉次特殊解には定数がつかないこともポイントです。実際にその特殊解を2倍して代入してみましょう。すると微分方程式は成り立ちませんし、成り立たない理由も分かるはずです。また非斉次特殊解を求めるための試行解は微分方程式の右辺 $r(x)$ の形を見て判断しますが、ある程度のパターンを知っておく必要があります。これらの例題はそのパターンの一部といえます。
この方法でどこまで通用するかというのは、パターンをどれだけ知っているか、あるいは見抜けるかにかかっています。そういう意味では職人技といえます。次回はもっと機械的に特殊解を導く方法を解説します。
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
常微分シリーズ過去記事
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
