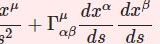\begin{equation}I_n\equiv \int_{-\infty}^\infty\frac{dx}{(1+x^2)^{n+1}} \quad (n\in\NN)\tag{1}\end{equation}
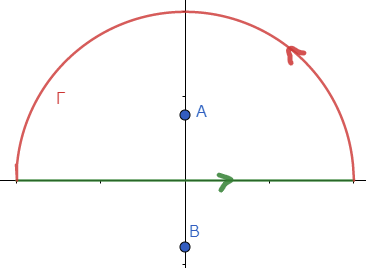
複素平面上で以下のように半径 $R$ の半円およびその弦を閉曲線 $C$ とします.弧を $\G$ と名付けておきます.
$C$ 上の周回積分は$$\oint_C\frac{dz}{(1+z^2)^{n+1}}=\int_{-R}^R\frac{dx}{(1+x^2)^{n+1}}+\int_\Gamma\frac{dz}{(1+z^2)^{n+1}}$$と表されるので,$R\to\infty$ の極限をとれば右辺第1項が求めたい $I_n$ となることが分かります.図の点AおよびBは被積分関数の極であり,値は $\pm i$ です.
$\Gamma$ 上の積分
半円弧 $\Gamma$ での積分値$$\int_\Gamma\frac{dz}{(1+z^2)^{n+1}} $$を求めます.$z=Re^{i\theta}$ と置換すると\begin{eqnarray*}\left|\int_\Gamma\frac{dz}{(1+z^2)^{n+1}}\right|&=&\left|\int_0^\pi\frac{iRe^{i\theta}}{(1+R^2e^{2i\theta})^{n+1}}d\theta\right|\\&\le&\int_0^\pi\left|\frac{iRe^{i\theta}}{(1+R^2e^{2i\theta})^{n+1}}\right|d\theta\\&=&\int_0^\pi\left|\frac{R}{(1+R^2e^{2i\theta})^{n+1}}\right|d\theta\\&=& \int_0^\pi\frac{R}{(1+R^4+2R^2\cos^22\t)^\frac{n+1}{2}}d\theta\\&<& \int_0^\pi\frac{R}{R^{2n+2}}d\theta\\&=& \frac{\pi}{R^{2n+1}}\\ &\to& 0\quad(\mathrm{as}\quad R\to\infty)\end{eqnarray*}よって $0$ となります。
周回積分
次に周回積分を計算します.$R$ が十分に大きければ閉曲線 $C$ の内部に点A$(i)$があります.被積分関数 $f(z)$ に関して$$f(z)\equiv\frac{1}{(1+z^2)^{n+1}}=\frac{1}{(z+i)^{n+1}(z-i)^{n+1}}$$よって $f(z)$ は $C$ の内部に $(n+1)$ 位の極 $i$ を持ちます。それを除けば半円内(以下「領域 $D$」)で正則です.すなわち\begin{equation}g(z)\equiv\frac{1}{(z+i)^{n+1}}\tag{2}\end{equation}とおけば領域 $D$ 内で $g(z)$ は正則であり$$f(z)=\frac{g(z)}{(z-i)^{n+1}}$$とできます.
$g(z)$ は正則ですので $z=i$ まわりにテイラー展開できます.よって $f(z)$ は以下の形でローラン展開できるはずです.$$f(z)=\frac{a_{-n-1}}{(z-i)^{n+1}}+\frac{a_{-n}}{(z-i)^{n}}+\cdots+a_0+a_1(z-i)+\cdots$$したがって$$f(z)(z-i)^{n+1}=a_{-n-1}+a_{-n}(z-i)+\cdots+a_{-1}(z-i)^n+\cdots$$これを $z$ について $n$ 回微分して $z=i$ を代入すると$$\frac{d^n}{dz^n}[f(z)(z-i)^{n+1}]\Big|_{z=i}=n!a_{-1}$$$$\therefore\; a_{-1}=\frac{1}{n!}\frac{d^ng}{dz^n}\Big|_{z=i}$$ここで(2)を $n$ 回微分して$$\frac{d^ng}{dz^n}=\frac{(2n)!}{n!}(-1)^n(z+i)^{-2n-1}$$$z=i$ を代入すれば$$\frac{d^ng}{dz^n}\Big|_{z=i}=\frac{(2n)!}{n!\cdot 2^{2n+1}i}$$を得ます。よって$$a_{-1}=\frac{(2n)!}{(n!)^2\cdot 2^{2n+1}i}$$
最後に周回積分を実行します.$-1$ 次の項だけが積分値に寄与し,他はゼロです.\begin{eqnarray*}&&\oint_C\frac{dz}{(1+z^2)^{n+1}}\\ &=& \oint_C\left(\frac{a_{-n-1}}{(z-i)^{n+1}}+\frac{a_{-n}}{(z-i)^{n}}+\cdots+\frac{a_{-1}}{z-i}+a_0+a_1(z-i)+\cdots\right)dz\\ &=& \oint_C\frac{a_{-1}}{z-i}dz\\ &=& 2\pi i \cdot a_{-1} \\ &=& 2\pi i\cdot\frac{(2n)!}{(n!)^2\cdot 2^{2n+1}i}\\ &=& \frac{\pi(2n)!}{(n!)^2\cdot 2^{2n}}\end{eqnarray*}
結論
$$\oint_C\frac{dz}{(1+z^2)^{n+1}}=\int_{-R}^R\frac{dx}{(1+x^2)^{n+1}}+\int_\Gamma\frac{dz}{(1+z^2)^{n+1}}$$だったので $R$ の極限をとると$$\frac{\pi(2n)!}{(n!)^2\cdot 2^{2n}}=\int_{-\infty}^\infty\frac{dx}{(1+x^2)^{n+1}}+0$$これによって以下の結論となります.
$$\int_{-\infty}^\infty\frac{dx}{(1+x^2)^{n+1}}=\frac{\pi(2n)!}{(n!)^2\cdot 2^{2n}}$$
因みに,この値は$$\int_{-\infty}^\infty\frac{dx}{(1+x^2)^{n+1}}=\frac{(2n-1)!!}{(2n)!!}\pi$$とも書けます.
範囲が無限大までという広義積分であることを除けば,実は高等学校の置換積分で計算可能です.$x=\tan\theta$ として\begin{eqnarray*}\int_{-\infty}^\infty\frac{dx}{(1+x^2)^{n+1}}&=&2\int_0^\infty\frac{dx}{(1+x^2)^{n+1}}\\ &=&2\int_0^\frac{\pi}{2}\frac{1}{(\frac{1}{\cos^2\t})^{n+1}}\frac{d\t}{\cos^2\t}\\&=& 2\int_0^\frac{\pi}{2}\cos^{2n}\t d\t \\ &=&2\frac{\pi}{2}\frac{(2n-1)!!}{(2n)!!}\\&=& \pi\frac{(2n-1)!!}{(2n)!!} \end{eqnarray*}先ほどの結論と一致します.
ほかにもどうぞ!
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。