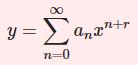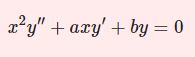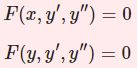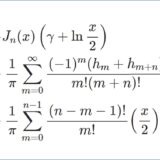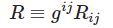\begin{equation}x^2y^{\prime\prime}+2xy'+\left[x^2-\nu(\nu+1)\right]y=0\tag{1}\end{equation}
これは球座標でのヘルムホルツ方程式を変数分離で解くときに,動径成分の方程式として現れます.ヘルムホルツ方程式から(1)が現れる過程については
を参照ください.「球ベッセル」と名付けられるのは,ベッセルの微分方程式との類似性や関わりがあるからです.ベッセルの微分方程式およびその解であるベッセル関数についての詳細は
を参照ください.
$$y=\sum_{n=0}^\infty a_nx^{n+r}\;,\; a_0\neq 0$$とおくと\begin{eqnarray*}y'&=&\sum_{n=0}^\infty (n+r)a_nx^{n+r-1}\\y^{\prime\prime}&=&\sum_{n=0}^\infty (n+r)(n+r-1)a_nx^{n+r-2}\end{eqnarray*}これらを微分方程式(1)に代入すると $x^r$ の係数は $(r-\nu)(r+\nu+1)a_0=0$ となります(決定方程式).$a_0\neq 0$ ですから $r=\nu,-\nu-1$ となります.
$r=\nu$ としてあらためて $$y=\sum_{n=0}^\infty a_nx^{n+\nu}\;,\; a_0\neq 0$$とおきます.微分方程式(1)に代入すると$$2(\nu+1)a_1x+ \sum_{n=2}^\infty \left[n(n+2\nu+1)a_n+a_{n-2}\right]x^n=0$$$$\therefore\;\begin{cases}a_1 &=& 0 \\ a_{n}&=&\displaystyle\frac{-1}{n(n+2\nu+1)}a_{n-2}\end{cases}$$奇数項はすべてゼロとなります. よって$$\begin{cases}a_{2m-1} &=& 0 \\ a_{2m}&=&\displaystyle\frac{-1}{2m(2m+2\nu+1)}a_{2m-2}\quad(m\ge 1)\end{cases}$$偶数項の漸化式を繰り返し用いれば \begin{eqnarray*}a_{2m}&=& \frac{-1}{2m(2m+1)}a_{2m-2} \\ &\vdots& \\ &=& \frac{(-1)^m}{(2m)!!\cdot (2m+2\nu+1)(2m+2\nu-1)\cdots(2\nu+3)}a_0 \quad(m\ge 1) \\ &=& \frac{(-1)^m}{2^{2m}m!\cdot (m+\nu+\frac{1}{2})(m+\nu-\frac{1}{2})\cdots(\nu+\frac{3}{2})}a_0 \\&=& a_0\frac{(-1)^m\Gamma(\nu+\frac{3}{2})}{2^{2m}m!\Gamma(m+\nu+\frac{3}{2})}\quad (m\ge 0)\end{eqnarray*}$a_0=\displaystyle\frac{\sqrt{\pi}}{2^{\nu+1}\Gamma(\nu+\frac{3}{2})}$ ととると$$a_{2m}= \frac{(-1)^m\sqrt{\pi}}{2^{2m+\nu+1}m!\Gamma(m+\nu+\frac{3}{2})}$$よって微分方程式の特殊解 $y_1(x)$ は\begin{eqnarray*}y_1(x)&=& \sum_{m=0}^\infty \frac{(-1)^m\sqrt{\pi}}{2^{2m+\nu+1}m!\Gamma(m+\nu+\frac{3}{2})} x^{2m+\nu}\\ &=& \sqrt{\frac{\pi}{2x}} J_{\nu+\frac{1}{2}}(x)\end{eqnarray*}ここで $J_\nu(x)$ は第1種ベッセル関数であり$$J_\nu(x)=\sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m+\nu}$$と級数表示されます.この特殊解を第1種球ベッセル関数 $j_\nu(x)$ と定義します("spherical Bessel functions of the first kind").
微分方程式(1)の1つの特殊解は「第1種球ベッセル関数」\begin{equation}j_\nu(x)=\sqrt{\frac{\pi}{2x}} J_{\nu+\frac{1}{2}}(x)\tag{2}\end{equation}である.ただし $J_\nu(x)$ は第1種ベッセル関数.
「ベッセルの微分方程式」の2つの独立な特殊解は $J_\nu(x)$ と $Y_\nu(x)$ でした.後者を「第2種ベッセル関数」あるいは「ノイマン関数」といいます.(2)に示した $J_\nu(x)$ と $j_\nu(x)$ の関係と同様に,(1)のもう1つの特殊解 $n_\nu(x)$ を以下のように定義します.これを第2種球ベッセル関数あるいは球ノイマン関数とよびます.
微分方程式(1)の1つの特殊解は「第2種球ベッセル関数」\begin{equation}n_\nu(x)=\sqrt{\frac{\pi}{2x}} Y_{\nu+\frac{1}{2}}(x)\tag{3}\end{equation}である.ただし $Y_\nu(x)$ は第2種ベッセル関数.
$j_\nu(x)$ と $n_\nu(x)$ はその定義から明らかに独立です.詳しくは冒頭の関連記事をご覧ください.
とはいっても(3)が本当に球ベッセル微分方程式(1)の解なのかは確かめる必要があります.まず $Y_{\nu+\frac{1}{2}}(x)$ (※ 以下単に $Y$ とする)は $\nu+\frac{1}{2}$ 次のベッセルの微分方程式の解ですから$$x^2Y^{\prime\prime}+xY'+\left[x^2-\left(\nu+\frac{1}{2}\right)^2\right]Y=0$$を満たします.ここで(3)を(1)の左辺に代入すると\begin{eqnarray*}&&x^2n_\nu^{\prime\prime}+2xn_\nu^\prime+[x^2-\nu(\nu+1)]n_\nu\\&=&x^2\sqrt{\frac{\pi}{2x}}Y^{\prime\prime}-x\sqrt{\frac{\pi}{2x}}Y'+\frac{3}{4}\sqrt{\frac{\pi}{2x}}Y+2x\sqrt{\frac{\pi}{2x}}Y'-\sqrt{\frac{\pi}{2x}}Y+\left[x^2-\left(\nu+\frac{1}{2}\right)^2+\frac{1}{4}\right]\sqrt{\frac{\pi}{2x}}Y\\&=&\sqrt{\frac{\pi}{2x}}\left[x^2Y^{\prime\prime}+xY'+\left[x^2-\left(\nu+\frac{1}{2}\right)^2\right]Y\right]+\frac{1}{4}\sqrt{\frac{\pi}{2x}}Y+\frac{3}{4}\sqrt{\frac{\pi}{2x}}Y-\sqrt{\frac{\pi}{2x}}Y\\&=&0\end{eqnarray*}よって $n_\nu(x)$ は(1)を満たすので特殊解です.
ここまでをまとめると
球ベッセルの微分方程式\begin{equation}x^2y^{\prime\prime}+2xy'+\left[x^2-\nu(\nu+1)\right]y=0\tag{1}\end{equation}の独立な2つの特殊解は,
第1種球ベッセル関数(球ベッセル関数)\begin{equation}j_\nu(x)=\sqrt{\frac{\pi}{2x}} J_{\nu+\frac{1}{2}}(x)\tag{2}\end{equation}
第2種球ベッセル関数(球ノイマン関数)\begin{equation}n_\nu(x)=\sqrt{\frac{\pi}{2x}} Y_{\nu+\frac{1}{2}}(x)\tag{3}\end{equation}
なお,ここで $J_\nu$ と $Y_\nu$ は第1種および第2種ベッセル関数であり,\begin{equation}J_\nu(x)=\sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m+\nu}\tag{4}\end{equation}\begin{equation}Y_\nu(x)=\frac{\cos\nu\pi\,J_\nu(x)-J_{-\nu}(x)}{\sin\nu\pi}\tag{5}\end{equation}
次は2つの球ベッセル関数の具体的な形を見ていきましょう.$\nu$ は一般に実数ですが,非負整数 $\nu=n$ のときを考えます.$J_{\nu+1/2}$ および $Y_{\nu+1/2}$ は初等関数で表されるので $j_n(x)$ と $n_n(x)$ も初等関数で表現可能です.
$j_n(x)$ を調べる
(2)(4)より\begin{eqnarray*}j_n(x)&=&\frac{\sqrt{\pi}}{2}\sum_{m=0}^\infty\frac{(-1)^m}{m!\G(m+n+\frac{3}{2})}\left(\frac{x}{2}\right)^{2m+n}\\&=&\frac{\sqrt{\pi}}{2}\sum_{m=0}^\infty\frac{(-1)^m}{m!(m+n+\frac{1}{2})(m+n-\frac{1}{2})\cdots\frac{1}{2}\sqrt{\pi}}\left(\frac{x}{2}\right)^{2m+n}\\&=&\sum_{m=0}^\infty\frac{(-1)^m}{m!(2m+2n+1)!!2^m}x^{2m+n}\\&=&\sum_{m=0}^\infty\frac{(-1)^m(m+n)!2^{m+n}}{m!(2m+2n)!!(2m+2n+1)!!2^m}x^{2m+n}\\&=&\sum_{m=0}^\infty\frac{(-1)^m(m+n)!2^{n}}{m!(2m+2n+1)!}x^{2m+n}\\&=&(2x)^n\sum_{m=0}^\infty\frac{(-1)^m(m+n)!}{m!(2m+2n+1)!}x^{2m}\end{eqnarray*}
\begin{equation}\therefore\quad j_n(x)=(2x)^n\sum_{m=0}^\infty\frac{(-1)^m(m+n)!}{m!(2m+2n+1)!}x^{2m}\tag{6}\end{equation}
これを用いて具体的に関数形を求めると\begin{eqnarray*}j_0(x)&=&\frac{\sin x}{x}\\[1em]j_1(x)&=&2x\sum_{m=0}^\infty\frac{(-1)^m(m+1)}{(2m+3)!}x^{2m}\\&=&\sum_{m=0}^\infty\frac{(-1)^m(2m+2)}{(2m+3)!}x^{2m+1}\\&=&\sum_{m=1}^\infty\frac{(-1)^{m-1}2m}{(2m+1)!}x^{2m-1}\\&=&-\sum_{m=0}^\infty\frac{(-1)^m[(2m+1)-1]}{(2m+1)!}x^{2m-1}\\&=&\sum_{m=0}^\infty\frac{(-1)^m}{(2m+1)!}x^{2m-1}-\sum_{m=0}^\infty\frac{(-1)^m}{(2m)!}x^{2m-1}\\&=&\frac{\sin x}{x^2}-\frac{\cos x}{x}\\[1em]j_2(x)&=&4x^2\sum_{m=0}^\infty\frac{(-1)^m(m+2)!}{m!(2m+5)!}x^{2m}\\&=&\sum_{m=0}^\infty\frac{(-1)^m}{(2m+5)!}\left[(2m+5)(2m+4)-3(2m+5)+3\right]x^{2m+2}\\&=&-\frac{1}{x}(\sin x -x)-\frac{3}{x^2}\left(\cos x-1+\frac{x^2}{2}\right)+\frac{3}{x^3}\left(\sin x-x+\frac{x^3}{6}\right)\\&=&\frac{(3-x^2)\sin x-3x\cos x}{x^3}\end{eqnarray*}このようにサイン・コサインに多項式をかけたものとなります.一般には
\begin{eqnarray*}j_n(x)&=&\frac{1}{x}\Biggl[\sum_{m=0}^{[\frac{n}{2}]}\frac{(-1)^m(n+2m)!}{(2m)!(n-2m)!(2x)^{2m}}\sin\left(x-\frac{n\pi}{2}\right)\\&&+\sum_{m=0}^{[\frac{n-1}{2}]}\frac{(-1)^m(n+2m+1)!}{(2m+1)!(n-2m-1)!(2x)^{2m+1}}\cos\left(x-\frac{n\pi}{2}\right)\Biggr]\end{eqnarray*}
形だけでももう少しすっきり表せる式はないものか.$\sin$ のマクローリン展開から$$\frac{\sin x}{x}=\sum_{m=0}^\infty\frac{(-1)^m}{(2m+1)!}(x^2)^m$$これを $x^2$ について $n$ 回微分します.\begin{eqnarray*}\frac{d^n}{d(x^2)^n}\frac{\sin x}{x}&=&\sum_{m=n}^\infty\frac{(-1)^m}{(2m+1)!}m(m-1)\cdots(m-n+1)(x^2)^{m-n}\\&=&\sum_{m=0}^\infty\frac{(-1)^{m+n}(m+n)!}{m!(2m+2n+1)!}x^{2m}\end{eqnarray*}これと(6)を見比べると$$j_n(x)=(-1)^n(2x)^n\frac{d^n}{d(x^2)^n}\frac{\sin x}{x}$$
$$\therefore\quad j_n(x)=(-1)^nx^n\left(\frac{1}{x}\frac{d}{dx}\right)^n\frac{\sin x}{x}$$
実用性はともかく,初等関数で表せることをややスッキリ示せている式かなと思います.
$n_n(x)$ を調べる
(3)(4)(5)より\begin{eqnarray*}n_n(x)&=&\sqrt{\frac{\pi}{2x}}Y_{\nu+1/2}(x) \\&=& \sqrt{\frac{\pi}{2x}}\frac{\cos(n+\frac{1}{2})\pi\,J_{n+1/2}(x)-J_{-n-1/2}(x)}{\sin(n+\frac{1}{2})\pi}\\&=&\sqrt{\frac{\pi}{2x}}\frac{-J_{-n-1/2}(x)}{(-1)^n}\\&=&\sqrt{\frac{\pi}{2x}}(-1)^{n+1}\sum^\infty_{m=0}\frac{(-1)^m}{m! \G(m-n+\frac{1}{2})}\left(\frac{x}{2}\right)^{2m-n-\frac{1}{2}}\\&=&\frac{\sqrt{\pi}}{2}(-1)^{n+1}\sum^\infty_{m=0}\frac{(-1)^m}{m! \G(m-n+\frac{1}{2})}\left(\frac{x}{2}\right)^{2m-n-1}\\&=&\frac{\sqrt{\pi}}{2}(-1)^{n+1}\left[\sum^{n-1}_{m=0}\frac{(-1)^m}{m! \G(m-n+\frac{1}{2})}\left(\frac{x}{2}\right)^{2m-n-1}+\sum^\infty_{m=n}\frac{(-1)^m}{m! \G(m-n+\frac{1}{2})}\left(\frac{x}{2}\right)^{2m-n-1}\right]\\&=&\frac{\sqrt{\pi}}{2}(-1)^{n+1}\left[\sum^{n-1}_{m=0}\frac{(-1)^m}{m! \frac{\sqrt{\pi}2^{n-m}}{(-1)^{n-m}(2n-2m-1)!!}}\left(\frac{x}{2}\right)^{2m-n-1}+\sum^\infty_{m=n}\frac{(-1)^m}{m! \frac{\sqrt{\pi}(2m-2n-1)!!}{2^{m-n}}}\left(\frac{x}{2}\right)^{2m-n-1}\right]\\&=&\frac{1}{2}(-1)^{n+1}\left[\sum^{n-1}_{m=0}\frac{(-1)^n(2n-2m-1)!!}{m!2^{n-m}}\left(\frac{x}{2}\right)^{2m-n-1}+\sum^\infty_{m=n}\frac{(-1)^m}{m!(2m-2n-1)!!2^{n-m}}\left(\frac{x}{2}\right)^{2m-n-1}\right]\\&=&\frac{1}{2}\left[-\sum^{n-1}_{m=0}\frac{(2n-2m)!}{m!2^{m-1}(2n-2m)!!}x^{2m-n-1}-(-1)^n\sum^\infty_{m=n}\frac{(-1)^m(2m-2n)!!}{m!2^{m-1}(2m-2n)!}x^{2m-n-1}\right]\\&=&\frac{1}{2x^{n+1}}\left[-\sum^{n-1}_{m=0}\frac{(2n-2m)!}{m!2^{n-1}(n-m)!}x^{2m}-(-1)^n\sum^\infty_{m=n}\frac{(-1)^m(m-n)!}{m!2^{n-1}(2m-2n)!}x^{2m}\right]\\&=&-\frac{1}{2^nx^{n+1}}\left[\sum^{n-1}_{m=0}\frac{(2n-2m)!}{m!(n-m)!}x^{2m}+(-1)^n\sum^\infty_{m=n}\frac{(-1)^m(m-n)!}{m!(2m-2n)!}x^{2m}\right]\end{eqnarray*}
\begin{equation}n_n(x)=-\frac{1}{2^nx^{n+1}}\left[\sum^{n-1}_{m=0}\frac{(2n-2m)!}{m!(n-m)!}x^{2m}+(-1)^n\sum^\infty_{m=n}\frac{(-1)^m(m-n)!}{m!(2m-2n)!}x^{2m}\right]\tag{7}\end{equation}
ただし $n=0$ のときは1つめのシグマを無視します.(7)によって具体的な関数形を求めると\begin{eqnarray*}n_0(x)&=&-\frac{\cos x}{x}\\n_1(x)&=&-\frac{\cos x+x\sin x}{x^2}\\&\vdots&\end{eqnarray*}やはりサイン・コサインが現れます.一般の $n$ においては
\begin{eqnarray*}n_n(x)&=&-\frac{1}{x}\Biggl[\sum_{m=0}^{[\frac{n}{2}]}\frac{(-1)^m(n+2m)!}{(2m)!(n-2m)!(2x)^{2m}}\cos\left(x-\frac{n\pi}{2}\right)\\&&+\sum_{m=0}^{[\frac{n-1}{2}]}\frac{(-1)^m(n+2m+1)!}{(2m+1)!(n-2m-1)!(2x)^{2m+1}}\sin\left(x-\frac{n\pi}{2}\right)\Biggr]\end{eqnarray*}
もう1つの等式を示しておきます.$\cos$ のマクローリン展開から$$\frac{\cos x}{x}=\sum_{m=0}^\infty\frac{(-1)^m}{(2m)!}(x^2)^{m-\frac{1}{2}}$$これを $x^2$ について $n$ 回微分します.\begin{eqnarray*}&&\frac{d^n}{d(x^2)^n}\frac{\cos x}{x}\\&=&\sum_{m=0}^\infty\frac{(-1)^m}{(2m)!}\left(m-\frac{1}{2}\right)\left(m-\frac{3}{2}\right)\cdots\left(m-n+\frac{1}{2}\right)(x^2)^{m-n-\frac{1}{2}}\\&=&\frac{1}{2^nx^{2n+1}}\sum_{m=0}^\infty\frac{(-1)^m}{(2m)!}(2m-1)(2m-3)\cdots(2m-2n+1)x^{2m}\\&=&\frac{1}{2^nx^{2n+1}}\Biggl[\sum_{m=0}^{n-1}\frac{(-1)^m(-1)(-3)\cdots(-(2n-2m-1))}{(2m)(2m-2)\cdots4\cdot2}x^{2m}\\&&\quad+\sum_{m=n}^\infty\frac{(-1)^m}{(2m)(2m-2)\cdots (2m-2n+2)\times (2m-2n)!}x^{2m}\Biggr]\\&=&\frac{1}{2^nx^{2n+1}}\Biggl[\sum_{m=0}^{n-1}\frac{(-1)^{n}(2n-2m-1)!!}{2^mm!}x^{2m}+\sum_{m=n}^\infty\frac{(-1)^m(2m-2n)!!}{(2m)!!(2m-2n)!}x^{2m}\Biggr]\\&=&\frac{1}{2^nx^{2n+1}}\left[(-1)^n\sum_{m=0}^{n-1}\frac{(2n-2m)!}{2^mm!(2n-2m)!!}x^{2m}+\sum_{m=n}^\infty\frac{(-1)^m(m-n)!}{m!(2m-2n)!2^n}x^{2m}\right]\\&=&\frac{1}{2^nx^{2n+1}}\left[(-1)^n\sum_{m=0}^{n-1}\frac{(2n-2m)!}{2^nm!(n-m)!}x^{2m}+\sum_{m=n}^\infty\frac{(-1)^m(m-n)!}{m!(2m-2n)!2^n}x^{2m}\right]\\&=&\frac{(-1)^n}{2^{2n}x^{2n+1}}\left[\sum_{m=0}^{n-1}\frac{(2n-2m)!}{m!(n-m)!}x^{2m}+(-1)^n\sum_{m=n}^\infty\frac{(-1)^m(m-n)!}{m!(2m-2n)!}x^{2m}\right]\end{eqnarray*}(7)と比べると$$n_n(x)=(-1)^{n+1}(2x)^n\frac{d^n}{d(x^2)^n}\frac{\cos x}{x}$$
$$\therefore\quad n_n(x)=(-1)^{n+1}x^n\left(\frac{1}{x}\frac{d}{dx}\right)^n\frac{\cos x}{x}$$
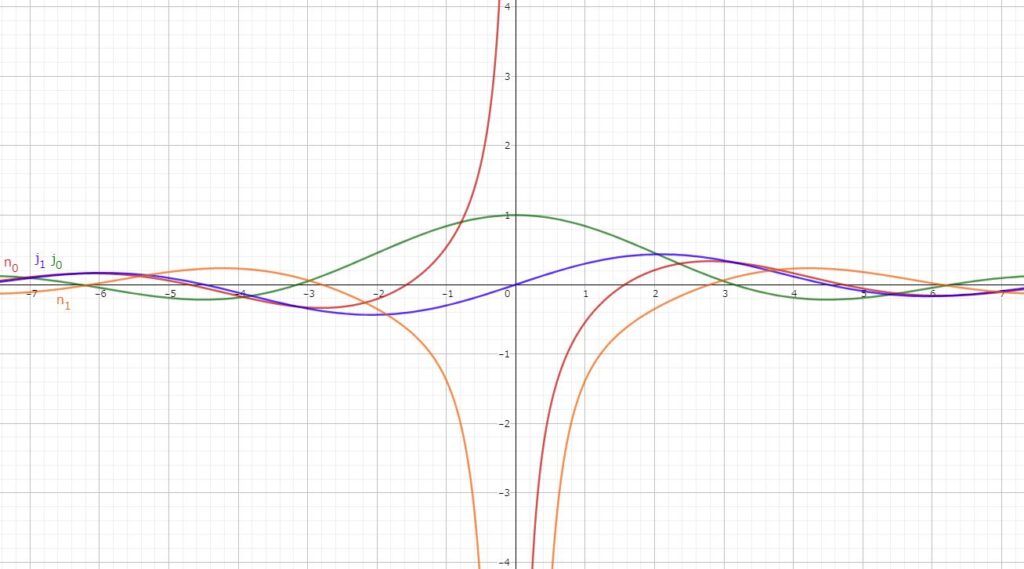
三角関数によって構成されているのが何となく分かりますね.
次?:
常微分方程式シリーズ
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。