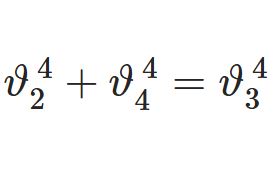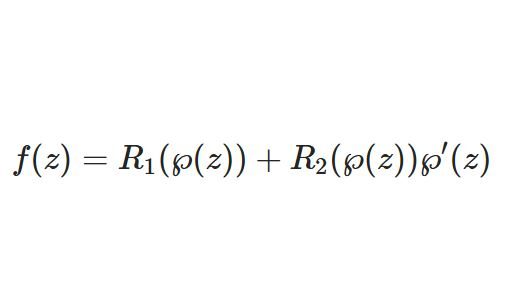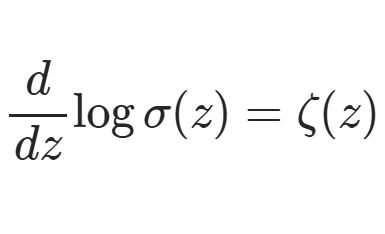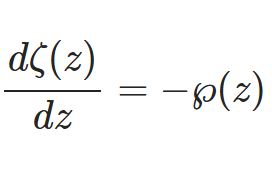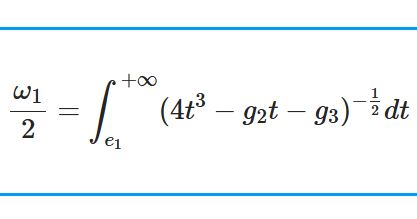複素積分演習（logの分岐点と切断）

複素積分の記事はほかにも、

などがあります。

Today's Theme

\begin{equation}I:=\int_0^\infty\frac{\ln x}{(x^2+4)^2}dx=\frac{\pi}{32}(\ln2-1)\tag{1A}\end{equation}\begin{equation}J:=\int_0^\infty\frac{x^{-b}}{x+a}dx=\frac{\pi}{a^b\sin\pi b}\tag{1B}\end{equation}ただし $a>0$ , $0<b<1$ .

複素積分としては基本的な部類です。今日はこれを留数定理によって示しましょう。

複素積分をつくる
周回積分の値を留数定理で求める
円弧の積分値を求める
偏角に注意して分岐点を扱う
２つめの積分
別の解法

複素積分をつくる

大体の場合、被積分関数の変数 $x$ をそのまま複素数 $z$ に変えたものを考えます。積分経路は上半平面の大円にしましょう。$\log z$ は $z=0$ に分岐点を持ちます。なので原点回りで1周することを禁止するために、複素平面の負の虚軸に切断を入れます。$$f(z):=\frac{\ln z}{(z^2+4)^2}\quad,\quad -\frac{\pi}{2}<\arg z<\frac{3}{2}\pi$$

半径 $R\to\infty$ の大円 $\G_1$ と半径 $\epsilon\to0$ の小円および実軸からなる経路です。これから$$\oint_C f(z)dz$$を考えることにより、進めていきます。

周回積分の値を留数定理で求める

$f(z)$ を見ると、$z=2i$ で2位の極を持ちます。よって留数は\begin{eqnarray*}a_{-1}&=&\left.\frac{d}{dz}(z-2i)^2f(z)\right|_{z=2i}\\&=& \left.\frac{d}{dz}\frac{\ln z}{(z+2i)^2}\right|_{z=2i} \\&=& \left[\frac{1}{z(z+2i)^2}-\frac{2\ln z}{(z+2i)^3}\right]_{z=2i} \\&=& \frac{i}{32}(1-\ln2)+\frac{\pi}{64}\end{eqnarray*}周回積分は $2\pi ia_{-1}$ ですから\begin{equation}\oint_C f(z)dz=\frac{\pi}{16}(\ln2-1)+\frac{\pi^2}{32}i\tag{2}\end{equation}

円弧の積分値を求める

大円 $\G_1$ の積分値を計算します。$z=Re^{i\t}$ とおき\begin{eqnarray*}\left|\int_{\G_1} f(z)dz\right| &=&\left|\int_0^\pi \frac{\ln R+i\t}{(R^2e^{2i\t}+4)^2}iRe^{i\t}d\t\right|\\ &\le& \int_0^\pi \frac{R|\ln R+i\t|}{|R^2e^{2i\t}+4|^2}d\t\end{eqnarray*}分母分子に三角不等式を用います。\begin{eqnarray*}\left|\int_{\G_1} f(z)dz\right| &\le& \int_0^\pi \frac{R|\ln R|+R|\t|}{|R^2-4|^2}d\t \\&=& \int_0^\pi \frac{R\ln R+R\t}{(R^2-4)^2}d\t \\ &\le& \int_0^\pi \frac{R\ln R+\pi R}{(R^2-4)^2}d\t \\&=& \pi\frac{R\ln R+\pi R}{(R^2-4)^2}\xrightarrow[]{R\to\infty}0\end{eqnarray*}よって\begin{equation}\int_{\G_1} f(z)dz=0\tag{3}\end{equation}

同様に小円弧 $\G_2$ は $z=\epsilon e^{i\t}$ とおき\begin{eqnarray*}\left|\int_{\G_2} f(z)dz\right| &=&\left|\int_0^\pi \frac{\ln \epsilon+i\t}{(\epsilon^2e^{2i\t}+4)^2}i\epsilon e^{i\t}d\t\right|\\ &\le& \int_0^\pi \frac{\epsilon|\ln \epsilon+i\t|}{|\epsilon^2e^{2i\t}+4|^2}d\t \\ &\le& \int_0^\pi \frac{\epsilon|\ln \epsilon|+\epsilon \t}{(\epsilon^2-4)^2}d\t \\&\le& \int_0^\pi \frac{\epsilon|\ln \epsilon|+\epsilon\pi}{(\epsilon^2-4)^2}d\t \\&=& \pi\frac{\epsilon|\ln \epsilon|+\epsilon\pi}{(\epsilon^2-4)^2}\xrightarrow[]{\epsilon\to +0}0\end{eqnarray*}したがって\begin{equation}\int_{\G_2} f(z)dz=0\tag{4}\end{equation}

偏角に注意して分岐点を扱う

最後に実軸上の積分区間をやります。負の区間では $\arg z=\pi$ なので $z=xe^{\pi i}$ として $x=\infty$ から $0$ まで積分します。正の区間では $\arg z=0 $ なので $z=x$ として $x=0$ から $\infty$ まで積分します。(3)(4)も併せて\begin{eqnarray*}\oint_C f(z)dz &=& \int_\infty^0\frac{\ln(xe^{\pi i})}{(x^2+4)^2}(-dx)+\int^\infty_0\frac{\ln x}{(x^2+4)^2}dx \\&=& 2\int^\infty_0\frac{\ln x}{(x^2+4)^2}dx+\pi i\int^\infty_0\frac{dx}{(x^2+4)^2}\end{eqnarray*}右辺第1項はまさに求めたい積分、第2項は $x=2\tan\t$ なる変換を施すとよいです。すると$$\oint_C f(z)dz =2I+\frac{\pi^2}{32}i$$となりますから、(2)と合わせて次の結論に達します。

\begin{equation}\int_0^\infty\frac{\ln x}{(x^2+4)^2}dx=\frac{\pi}{32}(\ln2-1)\tag{5}\end{equation}

２つめの積分

ここまでの知識を活かして $J$ も計算しましょう。 $a>0$ , $0<b<1$ の条件を忘れずに。

$x$ を $ax$ と置換すれば\begin{equation}J=\frac{1}{a^b}\int_0^\infty\frac{x^{-b}}{x+1}dx\tag{6}\end{equation}ここで\begin{equation}g(z):=\frac{z^{-b}}{z+1}\quad,\; 0<\arg z<2\pi\tag{7}\end{equation}と定めると $z=0$ が分岐点となるので、実軸の正の部分に切断を入れます。また $g(z)$ は $z=-1$ に1位の極を持ちます。次のように積分経路 $C$ を定めましょう。

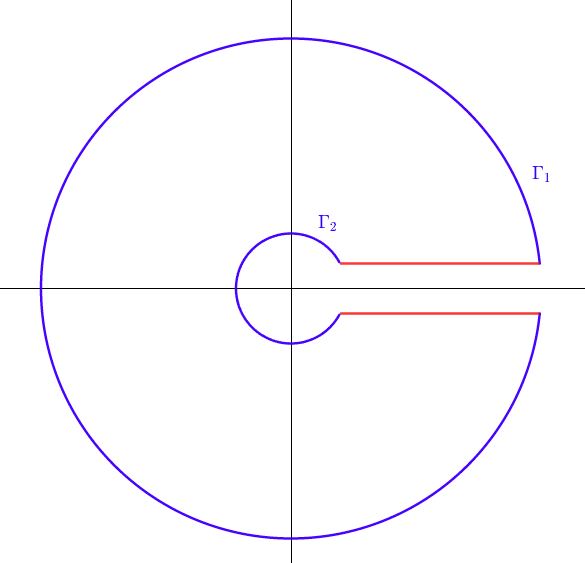
まず留数定理により\begin{equation}\oint g(z)dz=2\pi ie^{-ib\pi}\tag{8}\end{equation}となります。このとき、偏角の範囲に注意して $z=-1=e^{i\pi}$ として代入するとよいです。

大円弧は\begin{eqnarray*}\left|\int_{\G_1} g(z)dz\right| &\le& \int_0^{2\pi}\frac{R^{1-b}}{|Re^{i\t}+1|}d\t \\&\le& \int_0^{2\pi}\frac{R^{1-b}}{R-1}d\t \\ &=& 2\pi\frac{R^{1-b}}{R-1}\xrightarrow[]{R\to\infty}0\end{eqnarray*}小円弧も同様に\begin{eqnarray*}\left|\int_{\G_2} g(z)dz\right| &\le& \int_0^{2\pi}\frac{\epsilon^{1-b}}{|\epsilon e^{i\t}+1|}d\t \\&\le& \int_0^{2\pi}\frac{\epsilon^{1-b}}{1-\epsilon}d\t\\ &=& 2\pi\frac{\epsilon^{1-b}}{1-\epsilon}\xrightarrow[]{\epsilon\to0}0\end{eqnarray*}

実軸に沿った積分は $\arg z=0$ と $\arg z=2\pi$ であり、それぞれ $z=x$ , $z=xe^{2\pi i}$ と置換します。すなわち$$\oint g(z)dz=\int_0^\infty\frac{x^{-b}}{x+1}dx+\int_\infty^0\frac{(xe^{2\pi i})^{-b}}{x+1}dx$$(8)と合わせて整理すると$$\int_0^\infty\frac{x^{-b}}{x+1}dx=\frac{\pi}{\sin\pi b}$$を得ます。ガンマ関数の相反公式にも出てくる式です($\G(b)\G(1-b))$。(6)より

\begin{equation}\int_0^\infty\frac{x^{-b}}{x+a}dx=\frac{\pi}{a^b\sin\pi b}\tag{9}\end{equation}ただし $a>0$ , $0<b<1$ .

別の解法

(9)の導出は複素積分なしでも可能です。積分区間を $[0,1]$ と $[1,\infty)$ に分け、後者で $x\to\frac{1}{x}$ なる置換をします。その後 $\frac{1}{1+x}$ を級数展開します。級数を偶奇で分け、ディガンマ関数を登場させます。最後にディガンマ関数の相反公式を用います。\begin{eqnarray*}\int_0^\infty\frac{x^{-b}}{x+1}dx &=& \int_0^1\frac{x^{-b}+x^{b-1}}{1+x}dx \\&=& \sum_{n=0}^\infty (-1)^n\left(\frac{1}{n-b+1}+\frac{1}{n+b}\right) \\&=& \sum_{n=0}^\infty \left(\frac{1}{2n-b+1}+\frac{1}{2n+b}-\frac{1}{2n-b+2}-\frac{1}{2n+b+1}\right) \\&=& \frac{1}{2} \sum_{n=0}^\infty\left(\frac{1}{n+\frac{1-b}{2}}+\frac{1}{n+\frac{b}{2}}-\frac{1}{n+1-\frac{b}{2}}-\frac{1}{n+\frac{b+1}{2}}\right) \\&=& \frac{1}{2}\left[-\psi\left(\frac{1-b}{2}\right)-\psi\left(\frac{b}{2}\right)+\psi\left(1-\frac{b}{2}\right)+\psi\left(\frac{1+b}{2}\right)\right]\\&=&\frac{\pi}{2}\left(\cot\frac{b\pi}{2}-\cot\frac{1+b}{2}\pi\right) \\&=& \frac{\pi}{2}\left(\cot\frac{b\pi}{2}+\tan\frac{b\pi}{2}\right) \\&=&\frac{\pi}{\sin b\pi}\end{eqnarray*}ディガンマ関数については：

【γ9】ディガンマ関数の相反公式・倍数公式と特殊値・ゼータ関数（ガンマ関数の基礎シリーズ9）

本記事では下記の本を大いに参考にしています。複素解析を広く扱い、練習問題も豊富、計算の説明も丁寧です。

Complex Variables and Applications (Brown and Churchill)

応援のおねがい

Please support me!

まめしば

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。

ご支援いただいた方は、こちらで確認できます。

◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。

◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。

OFUSEで応援を送る

◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。