cosやsinの中身がxのn乗である場合の積分値を検討する。複素積分によって求めたフレネル積分を一般化して考えることによって、求める積分値はガンマ関数を用いて表現できることが分かる。複素積分で使う経路は扇形であり、コーシーの積分定理を用いるため複素解析の練習にもなる。
以前の記事では $$\int^\infty_0\cos (x^2)dx\;,\;\int^\infty_0\sin (x^2)dx$$$$\int^\infty_0\cos (x^3)dx\;,\;\int^\infty_0\sin (x^3)dx$$ の値を計算しました。
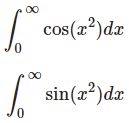【複素解析】フレネル積分-三角関数の特殊な積分 sin x^2 , cos x^2
【複素解析】cos(x^3),sin(x^3)の積分(扇形周回積分とガンマ関数)
これらで検討したことを活かし、三角関数 $\cos , \sin$ の引数が自然数 $n$ 乗となっている場合の積分をやってみます。
$n\geq 2$ とするとき、２つの定積分$$I_n=\displaystyle\int^\infty_0\cos (x^n)dx$$$$J_n=\displaystyle\int^\infty_0\sin (x^n)dx$$はいかなる値か．
過去記事での3乗の計算から明らかなように、初等的には解けずガンマ関数で表して終わることになります。方針としては、半径 $R$ で中心角 $\dfrac{\pi}{2n}$ の扇形を経路とした複素積分$$\oint_C e^{iz^n}dz$$を考えます。
被積分関数は閉曲線内で極をもたないため、コーシーの積分定理より周回積分は $0$ となります。扇形を $\Gamma_1$ , $\Gamma_2$ , $\Gamma_3$ の3つに分割して考えると$$0=\oint_Ce^{iz^n}dz=\int^R_0e^{ix^n}dx+\int_{\Gamma_2}e^{iz^n}dz+\int_{\Gamma_3}e^{iz^n}dz$$右辺第1項は$\Gamma_1$に関する積分です。この項について $R\to\infty$ の極限を考えると冒頭の $I_n,J_n$ が求まります。以下、問題形式で進めていきます。
$\Gamma_2$ の線積分において $z=Re^{i\theta}$ と置換し，$R\to\infty$ としたときの積分値を計算せよ．
$0\leq\theta\leq\pi/2n$ に注意します。置換して\begin{eqnarray*}\int_{\Gamma_2}e^{iz^n}dz &=& \int^{\frac{\pi}{2n}}_0iRe^{i\theta}e^{iR^n(\cos n\theta+i\sin n\theta)}d\theta\\&=& \int^{\frac{\pi}{2n}}_0iRe^{i\theta}e^{R^n(i\cos n\theta-\sin n\theta)}d\theta\end{eqnarray*}この結果の絶対値をとって評価すると\begin{eqnarray*}\left| \int^{\frac{\pi}{2n}}_0iRe^{i\theta}e^{R^n(i\cos n\theta-\sin n\theta)}d\theta \right| &=& \left| \int^{\frac{\pi}{2n}}_0Re^{i\theta}e^{iR^n\cos n\theta}e^{-R^n\sin n\theta}d\theta \right|\\ &\leq & \int^{\frac{\pi}{2n}}_0R\left| e^{i\theta}e^{iR^n\cos n\theta}e^{-R^n\sin n\theta}\right| d\theta\\ &=& \int^{\frac{\pi}{2n}}_0R\left| e^{-R^n\sin n\theta}\right| d\theta\xrightarrow[R\to\infty]{}0\end{eqnarray*}よって求める積分値は $0$ となります。
$\Gamma_3$の線積分において $z=e^{i\frac{\pi}{2n}}x$ と置換し，$R\to\infty$ としたときの積分値を計算せよ．
この $\Gamma_3$ は点 $Re^{i\frac{\pi}{2n}}$ から点 $0$ を結ぶ線分なので、$x$ の積分範囲は $R$ から$0$ となります。$z^n=e^{i\frac{\pi}{2}}x^n=ix^n$ より\begin{eqnarray*}\int_{\Gamma_3}e^{iz^n}dz &=& \int^0_Re^{-x^n}\cdot e^{\frac{\pi}{2n}i}dx\\ &\xrightarrow[R\to\infty]{}& -e^{\frac{\pi}{2n}i}\int^\infty_0e^{-x^n}dx\\ &=& -e^{\frac{\pi}{2n}i}\cdot \frac{1}{n}\Gamma\left(\frac{1}{n}\right)\end{eqnarray*}最後の等号ですが、これは $x^n=t$ とおいて\begin{eqnarray*}\int^\infty_0e^{-x^n}dx&=&\int^\infty_0e^{-t}\cdot \frac{1}{n}t^{\frac{1}{n}-1}dt\\ &=& \frac{1}{n}\Gamma\left(\frac{1}{n}\right)\end{eqnarray*}としたものです。上記の変形にはガンマ関数の定義$$\Gamma(x)=\int^\infty_0e^{-t}t^{x-1}dt$$を用いています。
これで$\Gamma_3$の積分が終わりました。
以上の結果から，冒頭の $I_n$ および $J_n$ を求めよ．
周回積分の３分割を再度示すと$$0=\oint_Ce^{iz^n}dz=\int^R_0e^{ix^n}dx+\int_{\Gamma_2}e^{iz^n}dz+\int_{\Gamma_3}e^{iz^n}dz$$$R\to\infty$ とし $\Gamma_2$ と $\Gamma_3$ の積分値を代入すると$$0=\int^\infty_0e^{ix^n}dx+0-e^{\frac{\pi}{2n}i}\cdot \frac{1}{n}\Gamma\left(\frac{1}{n}\right)$$すなわち$$\int^\infty_0e^{ix^n}dx=e^{\frac{\pi}{2n}i}\cdot \Gamma\left(\frac{1}{n}+1\right)$$$$\therefore \:\int^\infty_0 e^{ix^n}dx=\Gamma\left(\frac{1}{n}+1\right)\cos\frac{\pi}{2n}+i\Gamma\left(\frac{1}{n}+1\right)\sin\frac{\pi}{2n}$$$e^{ix^n}=\cos(x^n)+i\sin(x^n)$より、両辺の実部と虚部を比べると以下の結論を得ます。
$$\int^\infty_0\cos (x^n)dx=\Gamma\left(\frac{1}{n}+1\right)\cos\frac{\pi}{2n}$$$$\int^\infty_0\sin (x^n)dx=\Gamma\left(\frac{1}{n}+1\right)\sin\frac{\pi}{2n}$$
これでおしまいです。やはりガンマ関数が残りますので「値を求めた」とは言えませんが、見通しのよい形で表せていると思います。$n=2$ のときは半整数のガンマ関数になるので $\sqrt\pi$ に書き換えられますが、あくまで例外です。
似た方法で計算する積分はこちら：
$\int e^{-x^n}\sin(x^n)dx$ の積分（ガンマ関数）
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
