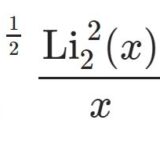シリーズ前回はこちら:
調和数を含んだ級数(Euler-sum)とゼータ関数 part16
ただし、本記事はむしろ次の記事のつづきという位置づけです:
今回はweight5のEuler-sumで、分母に $2^n$ が入っているもの$$\sum\frac{H_n^{(p)}}{n^q2^n}$$を取り上げます。
こちらの2023/2/9と同様にすると\begin{equation}\int_0^\frac{1}{2}\frac{\Li_2^{~2}(x)}{x}dx=2\sum_{n=1}^\infty\frac{H_{n-1}^{(2)}}{n^32^n}+4\sum_{n=1}^\infty\frac{H_{n-1}}{n^42^n}\tag{1}\end{equation}こちらの記事から\begin{align}\int_0^\frac{1}{2}\frac{\Li_2^{~2}(x)}{x}dx&=\frac{27}{32}\zeta(5)-2\Li_5\left(\frac{1}{2}\right)-2\Li_4\left(\frac{1}{2}\right)\ln2-\frac{5}{8}\zeta(4)\ln 2\\&\quad+\frac{7}{8}\zeta(3)\zeta(2)-\frac{7}{8}\zeta(3)\ln^22+\frac{1}{2}\zeta(2)\ln^32-\frac{7}{60}\ln^52\tag{2}\end{align}であったことと、こちらの記事で\begin{align} \sum_{n=1}^\infty\frac{H_n}{n^42^n}=& 2\Li_5\left(\frac{1}{2}\right)+\frac{1}{32}\zeta(5)+\Li_4\left(\frac{1}{2}\right)\ln2-\frac{\zeta(4)}{8}\ln2\\&+\frac{\zeta(3)}{2}\ln^22-\frac{\zeta(2)}{6}\ln^32-\frac{1}{2}\zeta(2)\zeta(3)+\frac{\ln^52}{40}\tag{3}\end{align}(2)(3)を(1)に適用して
\begin{align}\sum_{n=1}^\infty\frac{H_{n}^{(2)}}{n^32^n}&=\frac{23}{64}\zeta(5)-2\Li_5\left(\frac{1}{2}\right)-3\Li_4\left(\frac{1}{2}\right)\ln2-\frac{1}{16}\zeta(4)\ln 2\\&\quad+\frac{23}{16}\zeta(3)\zeta(2)-\frac{23}{16}\zeta(3)\ln^22+\frac{7}{12}\zeta(2)\ln^32-\frac{13}{120}\ln^52\end{align}
$\ln(1-x)$ や 多重対数関数 $\Li_p(x)$ のコーシー積をとることにより、同一weight間のEuler-sumの関係式を得ることができます。過去にはこちらの記事のようなことをしました。
今回は以下のようにします。\begin{align}-\ln(1-x)\Li_4(x) &=\left(\sum_{n=1}^\infty\frac{x^n}{n}\right)\left(\sum_{n=1}^\infty\frac{x^n}{n^4}\right)\\&=\sum_{n=2}^\infty\sum_{m=1}^{n-1}\frac{x^n}{m^4(n-m)}\end{align}部分分数分解して\begin{align}&=\sum_{n=2}^\infty\frac{x^n}{n}\sum_{m=1}^{n-1}\frac{1}{m^3}\left(\frac{1}{m}+\frac{1}{n-m}\right)\\&=\sum_{n=2}^\infty\frac{H_{n-1}^{(4)}}{n}x^n+\sum_{n=2}^\infty\frac{x^n}{n}\sum_{m=1}^{n-1}\frac{1}{m^3(n-m)}\\&=\sum_{n=2}^\infty\frac{H_{n-1}^{(4)}}{n}x^n+\sum_{n=2}^\infty\frac{x^n}{n^2}\sum_{m=1}^{n-1}\frac{1}{m^2}\left(\frac{1}{m}+\frac{1}{n-m}\right)\\&=\sum_{n=2}^\infty\frac{H_{n-1}^{(4)}}{n}x^n+\sum_{n=2}^\infty\frac{H_{n-1}^{(3)}}{n^2}x^n+\sum_{n=2}^\infty\frac{x^n}{n^2}\sum_{m=1}^{n-1}\frac{1}{m^2(n-m)}\end{align}このように部分分数分解を繰り返していくと最終的に\begin{align}-\ln(1-x)\Li_4(x) &=-5\Li_5(x)+2\sum_{n=1}^\infty\frac{H_n}{n^4}x^n+\sum_{n=1}^\infty\frac{H_n^{(2)}}{n^3}x^n+\sum_{n=1}^\infty\frac{H_n^{(3)}}{n^2}x^n+\sum_{n=1}^\infty\frac{H_n^{(4)}}{n}x^n\tag{4}\end{align}(4)はweight5のEuler-sumが4つ並んでおり、それらの関係式が導けました。
ここでは(4)で $x=1/2$ とします。\begin{align}5\Li_5\left(\frac{1}{2}\right)+\Li_4\left(\frac{1}{2}\right)\ln 2 &=2\sum_{n=1}^\infty\frac{H_n}{n^42^n}+\sum_{n=1}^\infty\frac{H_n^{(2)}}{n^32^n}+\sum_{n=1}^\infty\frac{H_n^{(3)}}{n^22^n}+\sum_{n=1}^\infty\frac{H_n^{(4)}}{n2^n}\tag{5}\end{align}(5)の右辺を見てみると、第1項は(3)そのもの、第2項は先ほどの定理1、第4項は前回記事の\begin{align}\sum_{n=1}^\infty\frac{H_n^{(4)}}{n2^n} &=\frac{27}{32}\zeta(5)-\Li_5\left(\frac{1}{2}\right)-\Li_4\left(\frac{1}{2}\right)\ln2\\&\quad+\frac{7}{16}\zeta(3)\zeta(2)-\frac{7}{16}\zeta(3)\ln^22+\frac{1}{6}\zeta(2)\ln^32-\frac{1}{30}\ln^52\tag{6}\end{align}ですでに解決しています。よって残りの第3項が計算できます。
\begin{align}\sum_{n=1}^\infty\frac{H_{n}^{(3)}}{n^22^n}&=-\frac{81}{64}\zeta(5)+4\Li_5\left(\frac{1}{2}\right)+3\Li_4\left(\frac{1}{2}\right)\ln2+\frac{5}{16}\zeta(4)\ln 2\\&\quad-\frac{7}{8}\zeta(3)\zeta(2)+\frac{7}{8}\zeta(3)\ln^22-\frac{5}{12}\zeta(2)\ln^32+\frac{11}{120}\ln^52\end{align}
短いですが、今日はここまで。
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。