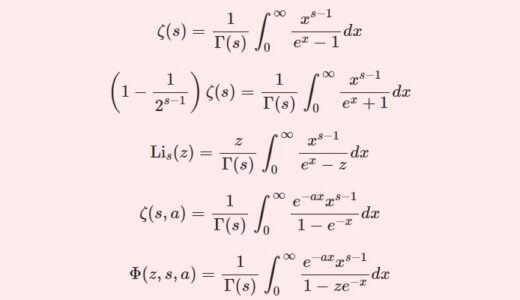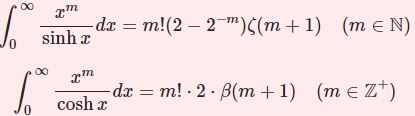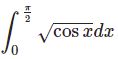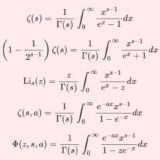$$\zeta(s)\equiv \sum_{n=1}^\infty\frac{1}{n^s}\quad (s\in\mathbb{C})$$において,$s$ が偶数のときの値を考える.
ここではフーリエ級数を用いる方法,その亜種としてパーセヴァルの等式を応用する方法,$\sin$ の無限乗積展開を用いる方法を紹介します.
$-\pi\le x\le\pi$ で定義された関数 $f(x)$ があるとします.これをフーリエ級数であらわすとその定義域において\begin{equation}f(x)=c+\sum_{n=1}^\infty a_n\cos nx+\sum_{n=1}^\infty b_n\sin nx\tag{1}\end{equation}となります.ここで\begin{eqnarray*}c &=& \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx\\ a_n &=&\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx\\ b_n &=&\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx\end{eqnarray*}です.これを応用してゼータを求めてみましょう.
$f(x)=x^2\quad (x\in[-\pi,\pi])$ をフーリエ級数展開し,$\zeta(2)$ を求めよ.
計算を始める前に $f(x)$ が偶関数であることに着目します.フーリエ級数展開したものももちろん偶関数ですから,(1)の奇関数部分の係数 $\{b_n\}$ はすべて$0$です(まともに計算してもそうなります).よって $c$ と $a_n$ のみ計算すればよいです。$$c=\frac{1}{2\pi}\int_{-\pi}^{\pi}x^2dx=\frac{\pi^2}{3}$$\begin{eqnarray*}a_n&=& \frac{1}{\pi}\int_{-\pi}^{\pi}x^2\cos nxdx\\ &=& \frac{2}{\pi}\int_{0}^{\pi}x^2\cos nxdx\\&=& \frac{4}{n^2}\cos n\pi\\ &=&\frac{4(-1)^n}{n^2}\end{eqnarray*}$n^2$ の逆数が見えますね.以上より $f(x)=x^2$ のフーリエ級数展開は$$x^2=\frac{\pi^2}{3}+\sum_{n=1}^\infty \frac{4(-1)^n}{n^2}\cos nx$$
両辺に $x=\pi$ を代入しましょう.$$\pi^2=\frac{\pi^2}{3}+\sum_{n=1}^\infty \frac{4(-1)^n}{n^2}(-1)^n$$変形すると$$\sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}$$よって$$\zeta(2)=\frac{\pi^2}{6}$$で終わりです.
$x=0$ を代入しても可です.\begin{eqnarray*}0&=&\frac{\pi^2}{3}+\sum_{n=1}^\infty \frac{4(-1)^n}{n^2}\\\Leftrightarrow \frac{\pi^2}{12}&=&-\sum_{n=1}^\infty \frac{(-1)^n}{n^2}\\&=&\left(\frac{1}{1^2}+\frac{1}{3^2}+\cdots\right)-\left(\frac{1}{2^2}+\frac{1}{4^2}+\cdots\right)\\&=& \left(\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}\cdots\right)-2\left(\frac{1}{2^2}+\frac{1}{4^2}+\cdots\right)\\&=& \zeta(2)-2\cdot\frac{1}{2^2}\left(\frac{1}{1^2}+\frac{1}{2^2}+\cdots\right)\\&=&\zeta(2)-\frac{1}{2}\zeta(2)\\&=& \frac{1}{2}\zeta(2)\end{eqnarray*}
※重積分を用いた方法はこちら:
$f(x)=x^4\quad (x\in[-\pi,\pi])$ をフーリエ級数展開し,$\zeta(4)$ を求めよ.
偶関数であることに注意して$$c=\frac{1}{2\pi}\int_{-\pi}^{\pi}x^4dx=\frac{\pi^4}{5}$$\begin{eqnarray*}a_n&=& \frac{1}{\pi}\int_{-\pi}^{\pi}x^4\cos nxdx\\ &=& \frac{2}{\pi}\int_{0}^{\pi}x^4\cos nxdx\\&=& (-1)^n\left(\frac{8\pi^2}{n^2}-\frac{48}{n^4}\right)\end{eqnarray*}$n^4$ の逆数が見えます.以上より $f(x)=x^4$ のフーリエ級数展開は$$x^4=\frac{\pi^4}{5}+\sum_{n=1}^\infty (-1)^n\left(\frac{8\pi^2}{n^2}-\frac{48}{n^4}\right)\cos nx$$両辺に $x=\pi$ を代入します.$$\pi^4=\frac{\pi^4}{5}+\sum_{n=1}^\infty \left(\frac{8\pi^2}{n^2}-\frac{48}{n^4}\right)$$整理して$$\frac{4\pi^4}{5}=8\pi^2\zeta(2)-48\zeta(4)$$$\zeta(2)=\frac{\pi^2}{6}$ でしたから$$\zeta(4)=\frac{\pi^4}{90}$$
同様に6次関数、8次関数・・・としていけば偶数のゼータ関数の値が求まっていきそうです.
ちなみに1次関数 $f(x)=x$ で同様のことをすると$$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}\cdots$$と,ゼータではありませんがゼータの交代級数バージョンみたいなものが得られます.3次関数でやってゼータがうまくできないことも確認してみてください.実際,奇数ゼータの値は未解決です.
(1)を2乗して $-\pi$ から $\pi$ まで積分すると,三角関数の直交性から\begin{eqnarray*}\int_{-\pi}^\pi f(x)^2dx&=&\int_{-\pi}^\pi\left( c+\sum_{n=1}^\infty a_n\cos nx+\sum_{n=1}^\infty b_n\sin nx \right)^2dx\\ &=& \int_{-\pi}^\pi \left[ c^2+2c\sum_{n=1}^\infty a_n\cos nx+2c\sum_{n=1}^\infty b_n\sin nx + \left(\sum_{n=1}^\infty a_n\cos nx\right)^2+\left( \sum_{n=1}^\infty b_n\sin nx\right)^2+2\left( \sum_{n=1}^\infty a_n\cos nx \right)\left( \sum_{n=1}^\infty b_n\sin nx \right)\right]dx \\&=& 2\pi c^2+0+0+ \pi\sum_{n=1}^\infty a_n^2+ \pi\sum_{n=1}^\infty b_n^2+0 \end{eqnarray*}よって以下が成立します.
\begin{equation} \int_{-\pi}^\pi f(x)^2dx = 2\pi c^2+ \pi\sum_{n=1}^\infty (a_n^2+ b_n^2)\tag{2}\end{equation}ただし \begin{eqnarray*}c &=& \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx\\ a_n &=&\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx\\ b_n &=&\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx\end{eqnarray*}
これと先ほどの例題を使って具体的なゼータを求めましょう.
$f(x)=x^2\quad (x\in[-\pi,\pi])$ より $\zeta(4)$ を求めよ.
例題1より $$c=\frac{\pi^2}{3}\;,\;a_n=\frac{4(-1)^n}{n^2}\;,\;b_n=0$$ (2)に代入して$$\int_{-\pi}^\pi x^4dx=2\pi\frac{\pi^4}{9}+\pi\sum_{n=1}^\infty\frac{16}{n^4}$$右辺第二項がゼータ関数ですね.$$\frac{2}{5}\pi^4=\frac{2}{9}\pi^4+16\zeta(4)$$$$\therefore\quad \zeta(4)=\frac{\pi^4}{90}$$
この方法では2次関数から $\zeta(4)$ があらわれました.ならば4次関数からだとどうなるでしょう?
$f(x)=x^4\quad (x\in[-\pi,\pi])$ より $\zeta(8)$ を求めよ. ただし $\zeta(6)=\dfrac{\pi^6}{945}$ である.
例題2より$$c= \frac{\pi^4}{5} \;,\; a_n= (-1)^n\left(\frac{8\pi^2}{n^2}-\frac{48}{n^4}\right) \;,\;b_n=0$$(2)に代入して $$\int_{-\pi}^\pi x^8dx=2\pi\frac{\pi^8}{25}+\pi\sum_{n=1}^\infty 64\left(\frac{\pi^2}{n^2}-\frac{6}{n^4}\right)^2$$計算を進めると$$\frac{2}{9}\pi^9=\frac{2}{25}\pi^9+64\pi\sum_{n=1}^\infty\left(\frac{\pi^4}{n^4}-\frac{12\pi^2}{n^6}+\frac{36}{n^8}\right)$$右辺に既知の $\zeta(4)$ , $\zeta(6)$ そして未知の $\zeta(8)$ が現れます.整理すると$$\zeta(8)=\frac{\pi^8}{9450}$$
オイラーによってはるか昔に用いられた方法です.$\sin x$ をテイラー展開すると\begin{equation}\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\end{equation}また $\sin x$ は $x=0,\pm n\pi$ でゼロとなることから,形式的に因数分解の要領で$$\sin x=x\left(1-\frac{x^2}{\pi^2}\right)\left(1-\frac{x^2}{4\pi^2}\right)\left(1-\frac{x^2}{9\pi^2}\right)\cdots$$(詳細はこちらから)よって
\begin{eqnarray*}&&x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots \\&=& x\left(1-\frac{x^2}{\pi^2}\right)\left(1-\frac{x^2}{4\pi^2}\right)\left(1-\frac{x^2}{9\pi^2}\right)\cdots\tag{3}\end{eqnarray*}
これの両辺を比較することでゼータ関数の値が求まります.例をみていきましょう.
(3)の3次の係数を比較することで $\zeta(2)$ を求めよ.
(3)の右辺において $x^3$ の項は,$x$ と,無数の $(1-\frac{x^2}{n^2\pi^2})$ から1つ $ -\frac{x^2}{n^2\pi^2} $を選んでかけたものの総和ですので$$-\frac{x^3}{6}=-\frac{x^3}{\pi^2} -\frac{x^3}{4\pi^2}-\frac{x^3}{9\pi^2}\cdots=\frac{-x^3}{\pi^2}\zeta(2)$$$$\therefore\quad\zeta(2)=\frac{\pi^2}{6}$$
(3)の5次の係数を比較することで $\zeta(4)$ を求めよ.
右辺の5次の項の係数は\begin{eqnarray*}&&\frac{1}{\pi^2}\left(\frac{1}{4\pi^2}+\frac{1}{9\pi^2}\cdots\right)+\frac{1}{4\pi^2}\left(\frac{1}{9\pi^2}+\frac{1}{16\pi^2}+\cdots\right)+\cdots\\&=&\frac{1}{\pi^4}\sum_{\substack{m,n=1\\m> n}}^\infty\frac{1}{m^2n^2}\end{eqnarray*} $m,n$ はひとまず別々ですべて和をとって,そこから $m=n$ の項を引いて $2!$ で割ればいいです($m<n$ を捨てるため).よって\begin{eqnarray*}\frac{1}{\pi^4}\sum_{\substack{m,n=1\\m> n}}^\infty\frac{1}{m^2n^2}&=&\frac{1}{2\pi^4}\left(\sum_{m=1}^\infty\sum_{n=1}^\infty\frac{1}{m^2n^2}-\zeta(4)\right)\\&=& \frac{1}{2\pi^4}\left( \zeta(2)^2-\zeta(4)\right)\\&=& \frac{1}{2\pi^4}\left( \frac{\pi^4}{36}-\zeta(4)\right)\end{eqnarray*}よって係数を比較して$$\frac{1}{120}=\frac{1}{2\pi^4}\left( \frac{\pi^4}{36}-\zeta(4)\right) $$$$\therefore\quad \zeta(4)=\frac{\pi^4}{90}$$
(3)の7次の係数を比較することで $\zeta(6)$ を求めよ.
右辺の7次の項は無限乗積での組み合わせを考えることにより\begin{eqnarray*}&&\frac{1}{3!\pi^6}\left[\sum_{i=1}^\infty\sum_{j=1}^\infty\sum_{k=1}^\infty\frac{1}{i^2j^2k^2}-3\sum_{i=1}^\infty\sum_{j=k=1}^\infty\frac{1}{i^2j^2k^2}+2\sum_{i=j=k=1}^\infty\frac{1}{i^2j^2k^2}\right]\\&=& \frac{1}{3!\pi^6}[\zeta(2)^3-3\zeta(2)\zeta(4)+2\zeta(6)]\\&=& \frac{1}{3!\pi^6} \left[\frac{\pi^6}{216}-\frac{\pi^6}{180}+2\zeta(6)\right]\end{eqnarray*}これが(3)左辺の $\dfrac{1}{7!}$ と一致します.計算すると$$\zeta(6)=\frac{\pi^6}{945}$$
次回はゼータ系の関数を4種類紹介し、その積分表示等を扱います:
それを応用した積分:
「ゼータ関数の基礎」シリーズを開講しました。複素解析を使っているので初等的ではありません。よかったら見てください:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。