Previous posts:
Integrals and Miscellaneous 15
Integrals and Miscellaneous 14
Integrals and Miscellaneous 13
Integrals and Miscellaneous 12
Integrals and Miscellaneous 11
Integrals and Miscellaneous 10
From (Almost) Impossible Integrals, Sums, and Series(Amazon)$$\sum_{n=1}^\infty\frac{H_n^{(p)}}{n^q}+\sum_{n=1}^\infty\frac{H_n^{(q)}}{n^p}=\zeta(p)\zeta(q)+\zeta(p+q)$$PROOF.\begin{eqnarray*}\sum_{n=1}^\infty\frac{H_n^{(p)}}{n^q} &=& \sum_{n=1}^\infty\sum_{k=1}^n\frac{1}{n^q k^p} \\&=& \sum_{k=1}^\infty\sum_{n=k}^\infty\frac{1}{n^q k^p} \\&=& \sum_{k=1}^\infty\frac{1}{k^p}\sum_{n=k}^\infty\frac{1}{n^q} \\&=& \sum_{k=1}^\infty\frac{1}{k^p}\left(\zeta(q)+\frac{1}{k^q}-H_{k}^{(q)}\right) \\&=& \zeta(q)\zeta(p)+\zeta(p+q)-\sum_{k=1}^\infty\frac{H_k^{(q)}}{k^p}\end{eqnarray*}Especially setting $p=q$ yields$$\sum_{n=1}^\infty\frac{H_n^{(p)}}{n^p}=\frac{1}{2}\left(\zeta(p)^2+\zeta(2p)\right)$$
$$\int_0^1\frac{\Li_2^2(t)}{t}dt=2\zeta(2)\zeta(3)-3\zeta(5)$$PROOF.
Cauchy's product of $\Li_2$ and $\Li_2$ is\begin{eqnarray*}\Li_2^2(t) &=& t^2\sum_{n=1}^\infty\sum_{m=1}^{n}\frac{t^{n-1}}{m^2(n-m+1)^2}\end{eqnarray*}\begin{eqnarray*}\therefore\quad\int_0^1\frac{\Li_2^2(t)}{t}dt &=& \sum_{n=1}^\infty\sum_{m=1}^{n}\frac{1}{m^2(n-m+1)^2}\int_0^1 t^n dt \\&=& \sum_{n=2}^\infty\sum_{m=1}^{n-1}\frac{1}{m^2n(n-m)^2} \\&=& \sum_{n=2}^\infty\frac{1}{n^3}\sum_{m=1}^{n-1}\left(\frac{1}{m}+\frac{1}{n-m}\right)^2 \\&=& \sum_{n=2}^\infty\frac{1}{n^3}\sum_{m=1}^{n-1}\left(\frac{1}{m^2}+\frac{1}{(n-m)^2}+\frac{2}{n}\left(\frac{1}{m}+\frac{1}{n-m}\right)\right) \\&=& \sum_{n=2}^\infty\frac{1}{n^3}\left(2H_{n-1}^{(2)}+\frac{4}{n}H_{n-1}\right) \\&=& 2\sum_{n=1}^\infty\frac{H_{n-1}^{(2)}}{n^3}+4\sum_{n=1}^\infty\frac{H_{n-1}}{n^4}\end{eqnarray*}The first sum is$$\sum_{n=1}^\infty\frac{H_{n-1}^{(2)}}{n^3}=3\zeta(2)\zeta(3)-\frac{11}{2}\zeta(5)$$which I proved "2023/2/11" below. And the second is$$\sum_{n=1}^\infty\frac{H_{n-1}}{n^4}=2\zeta(5)-\zeta(2)\zeta(3)$$which we obtained here. Hence we get$$\int_0^1\frac{\Li_2^2(t)}{t}dt=2\zeta(2)\zeta(3)-3\zeta(5)$$
From @MAGNA81407795:$$\prod_{n=1}^\infty\frac{(4n+3)(4n+15)}{(4n+6)(4n+12)}=\frac{512\sqrt{\pi}}{1155\G^2(\frac{3}{4})}$$PROOF.\begin{eqnarray} LHS &=& \frac{\G(\frac{5}{2})\G(4)}{\G(\frac{7}{4})\G(\frac{19}{4})}\lim_{n\to\infty}\frac{\G(\frac{7}{4}+n)\G(\frac{19}{4}+n)}{\G(\frac{5}{2}+n)\G(4+n)}\\ &=& \frac{\G(\frac{5}{2})\G(4)}{\G(\frac{7}{4})\G(\frac{19}{4})}\tag{1} \\&=& \frac{512\sqrt{\pi}}{1155\G^2(\frac{3}{4})}\end{eqnarray}We used the lemma that suppose $\sum_{i=0}^k a_i=\sum_{i=0}^k b_i$ then$$\lim_{z\to\infty}\frac{\G(z+a_1)\G(z+a_2)\cdots\G(z+a_k)}{\G(z+b_1)\G(z+b_2)\cdots\G(z+b_k)}=1$$proved here.
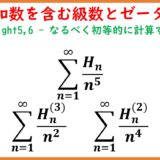
\begin{eqnarray}\sum_{n=1}^\infty\frac{H_n^{(2)}}{n^3} &=& -\frac{9}{2}\zeta(5)+3\zeta(2)\zeta(3) \\ \sum_{n=1}^\infty\frac{H_n^{(3)}}{n^2} &=& \frac{11}{2}\zeta(5)-2\zeta(2)\zeta(3)\end{eqnarray}
\begin{eqnarray*}\sum_{n=1}^\infty\frac{H_n}{n^5} &=& \frac{7}{4}\zeta(6)-\frac{1}{2}\zeta(5)\\\sum_{n=1}^\infty\frac{H_n^{(2)}}{n^4} &=& -\frac{1}{3}\zeta(6)+\zeta(3)^2\\\sum_{n=1}^\infty\frac{H_n^{(4)}}{n^2} &=& \frac{37}{12}\zeta(6)-\zeta(3)^2\end{eqnarray*}
\begin{eqnarray*}\sum_{k=1}^\infty\sum_{n=1}^\infty\frac{1}{n^3(n+k)^2} &=& \frac{9}{2}\zeta(5)-2\zeta(2)\zeta(3)\\\sum_{n=1}^\infty\sum_{k=1}^\infty\frac{1}{n^3(n+k)^3}&=&-\frac{1}{2}\zeta(6)+\frac{1}{2}\zeta(3)^2\\\sum_{n=1}^\infty\sum_{k=1}^\infty\frac{1}{n^4(n+k)^2}&=&\frac{25}{12}\zeta(6)-\zeta(3)^2\end{eqnarray*}PROOF here:
Theorems:$$\int_0^1 x^{n-1}\ln(1-x)dx=-\frac{H_n}{n}$$$$\int_0^1 x^{n-1}\ln^2(1-x)dx=\frac{H_n^2+H_n^{(2)}}{n}$$$$\int_0^1 x^{n-1}\ln^3(1-x)dx=-\frac{H_n^3+3H_nH_n^{(2)}+2H_n^{(3)}}{n}$$Lemmas:$$\sum_{k=1}^n\frac{H_k}{k} =\frac{H_n^2+H_n^{(2)}}{2}$$$$\sum_{k=1}^n\frac{H_k^2+H_k^{(2)}}{k}=\frac{H_n^3+3H_nH_n^{(2)}+2H_n^{(3)}}{3}$$
Abel's transformation:
Suppose $A_n:=\sum_{k=0}^n a_k$ then$$\sum_{k=m+1}^{m+n} a_kb_k=A_{m+n} b_{m+n+1}-A_m b_{m+1}+\sum_{k=m+1}^{m+n} A_k(b_k-b_{k+1})$$
PROOF:
$${}_3F_2\left[\begin{matrix}1,1,\nu+1\\2,\lambda+1\end{matrix};1\right] =\frac{\lambda}{\nu}\Bigl(\psi(\lambda)-\psi(\lambda-\nu)\Bigr)$$$${}_3F_2\left[\begin{matrix}1,1,1\\2,\lambda+1\end{matrix};1\right] =\lambda\zeta(2,\lambda)$$$${}_3F_2\left[\begin{matrix}1,1,1+a\\2,2+a\end{matrix};-1\right] = \frac{1+a}{a}\left(\psi(1+a)-\psi\left(1+\frac{a}{2}\right)\right)$$\begin{eqnarray}&&{}_4F_3\left[\begin{matrix}1,1,1+a,1+b\\2,\frac{a+3}{2},1+2b\end{matrix};1\right]\\&=&\frac{1+a}{2a}\left[\psi\left(\frac{1+a}{2}\right)-\psi\left(\frac{1}{2}\right)+\psi\left(b+\frac{1}{2}\right)-\psi\left(b+\frac{1-a}{2}\right)\right]\end{eqnarray}$${}_3F_2\left[\begin{matrix}1,1,1+a\\2,\frac{a+3}{2}\end{matrix};\frac{1}{2}\right] = \frac{1+a}{2a}\left[\psi\left(\frac{1+a}{2}\right)-\psi\left(\frac{1}{2}\right)\right]$$$${}_3F_2\left[\begin{matrix}1,1,1\\2,\frac{3}{2}\end{matrix};\frac{1}{2}\right] = \frac{\pi^2}{8}$$PROOF.
\begin{eqnarray}&&{}_4F_3\left[\begin{matrix}1,1,1+a,1+b\\2,2+a-b,2+a\end{matrix};1\right] \\&=& \frac{(1+a)(1+a-b)}{ab}\sum_{n=1}^\infty \frac{(a)_n(b)_n}{n(1+a-b)_n(1+a)_n} \\ &=& \frac{(1+a)(1+a-b)}{ab}\left[\psi\left(1+\frac{a}{2}\right)+\psi(1+a-b)-\psi(1+a)-\psi\left(1+\frac{a}{2}-b\right)\right]\end{eqnarray}
\begin{eqnarray}&&{}_5F_4\left[\begin{matrix}1,1,1+a,2+\frac{a}{2},1+b\\2+a,2,1+\frac{a}{2},2+a-b\end{matrix};-1\right] \\&=& -\frac{(1+a)(1+a-b)}{(2+a)b}\sum_{n=1}^\infty \frac{(a)_n(1+\frac{a}{2})_n(b)_n(-1)^n}{n(\frac{a}{2})_n(1+a-b)_n(1+a)_n} \\ &=& \frac{(1+a)(1+a-b)}{(2+a)b}\left[\psi(1+a)-\psi(1+a-b)\right]\end{eqnarray}
\begin{eqnarray}&&{}_8F_7\left[\begin{matrix}1,1,1+a,1+b,1+c,2+\frac{a}{2},2+2a-b-c+m,1-m\\2,1+\frac{a}{2},2+a-b,2+a-c,2+a,1+b+c-a-m,2+a+m\end{matrix};1\right] \\&=& -\frac{(1+a)(1+a-b)(1+a-c)(b+c-a-m)(1+a+m)}{bcm(2+a)(1+2a-b-c+m)}\\&&\times\Bigl[\psi(1+a-b)+\psi(1+a-c)+\psi(1+a+m)+\psi(1+a-b-c+m)\\&&\quad\quad-\psi(1+a)-\psi(1+a-b-c)-\psi(1+a-b+m)-\psi(1+a-c+m)\Bigr]\end{eqnarray}
\begin{eqnarray}&&{}_6F_5\left[\begin{matrix}1,1,a,b,c,\frac{3+c}{2}\\2,\frac{1+c}{2},1+c,2-a+c,2-b+c\end{matrix};1\right] \\&=& \frac{c(1-a+c)(1-b+c)}{(a-1)(b-1)(c+1)}\\&&\times\Bigl[\psi(1-a+c)+\psi(1-b+c)-\psi(c)-\psi(2+c-a-b)\Bigr]\end{eqnarray}
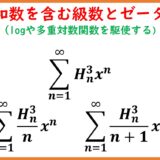
$$\sum_{n=1}^\infty H_n^{(p)}x^n=\frac{\Li_p(x)}{1-x}$$PROOF.
The cauthy product of the following two series:$$\Li_p(x)=\sum_{n=1}^\infty\frac{x^n}{n^p}\;,\;\frac{1}{1-x}=1+x+x^2+\cdots$$gives\begin{eqnarray*}\frac{\Li_p(x)}{1-x} &=& \left(\sum_{n=1}^\infty\frac{x^n}{n^p}\right)\left(\sum_{n=0}^\infty x^n\right) \\&=& \sum_{n=1}^\infty\left(\sum_{k=1}^n \frac{1}{k^p}\right)x^n \\&=&\sum_{n=1}^\infty H_n^{(p)}x^n\end{eqnarray*}
\begin{equation}\sum_{n=1}^\infty (H_n^2-H_n^{(2)})x^n=\frac{\ln^2(1-x)}{1-x}\tag{A}\end{equation}PROOF.
Recall the following formula$$\sum_{n=1}^\infty H_n^{(2)}x^n=\frac{\Li_2(x)}{1-x}$$proved "2023/2/18" above in this page, and $$\sum_{n=1}^\infty H_n^2x^n=\frac{\ln^2(1-x)+\Li_2(x)}{1-x}$$proved here. Then (A) follows.
$$\sum_{n=0}^\infty\frac{(2n)!!}{(2n+1)!!}\frac{(n+1)(2n+5)}{(2n+1)(2n+3)^2}=1$$$${}_4F_3\left[\begin{matrix}1,\frac{1}{2},\frac{1}{2},\frac{7}{2}\\\frac{5}{2},\frac{5}{2},\frac{5}{2}\end{matrix};1\right]=\frac{9}{5}$$
\begin{eqnarray*}{}_3F_2\left[\begin{matrix}1,1,\frac{1}{2}\\\frac{3}{2},\frac{3}{2}\end{matrix};1\right] &=& 2G\\{}_3F_2\left[\begin{matrix}1,1,\frac{3}{2}\\\frac{5}{2},\frac{5}{2}\end{matrix};1\right] &=& 18-18G\end{eqnarray*}PROOF:
$$I:=\int_0^\infty xe^{-x}\cos xdx=0$$$$J:=\int_0^\infty xe^{-x}\sin xdx=\frac{1}{2}$$PROOF. We define$$I(s):=\int_0^\infty e^{-sx}\cos xdx\;,\;J(s):=\int_0^\infty e^{-sx}\sin xdx$$to find $I=-I'(1)$ , $J=-J'(1)$. It follows from Laplace transforms that$$I(s)=\frac{s}{s^2+1}\;,\; J(s)=\frac{1}{s^2+1}$$and$$I'(s)=\frac{1-s^2}{(s^2+1)^2}\;,\; J(s)=\frac{-2s}{(s^2+1)^2}$$Hence,$$I=0\;,\;J=\frac{1}{2}$$
Simpler way: We can integrate directly.$$\int xe^{-x}\cos xdx=\frac{e^{-x}}{2}[(x+1)\sin x-x\cos x]+C$$$$\int xe^{-x}\sin xdx=-\frac{e^{-x}}{2}[(x+1)\cos x+x\sin x]+C$$
$$S:=\sum_{n=1}^\infty\frac{(-1)^n\ln n}{n}=\g\ln2-\frac{\ln^22}{2}$$PROOF.
We define $$f(s):=\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n^s}=\left(1-\frac{1}{2^{s-1}}\right)\zeta(s)$$to find $$S=\lim_{s\to0}f'(s+1)$$We obtained in the previous post that$$\displaystyle\lim_{s\to 1}\left(\zeta(s)-\frac{1}{s-1}\right)=\gamma$$Hence,$$\zeta(s)=\frac{1}{s-1}+\g+O(s-1)$$and we see easily that$$2^s=1+s\ln2+s^2\frac{\ln^22}{2}+O(s^3)$$$$\therefore\quad f(s+1)=\ln2+s\g\ln2-s\frac{\ln^22}{2}+O(s^2)$$Or$$f'(s+1)=\g\ln2-\frac{\ln^22}{2}+O(s)\xrightarrow[]{s\to 0}\g\ln2-\frac{\ln^22}{2}$$
From @Turkimath1:$$S:=\sum_{n=1}^\infty\frac{(-1)^n\ln^2 n}{n}=2\g_1\ln2+\g\ln^22-\frac{\ln^32}{3}$$PROOF.
We define $$f(s):=\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n^s}=\left(1-\frac{1}{2^{s-1}}\right)\zeta(s)$$to find $$S=-\lim_{s\to0}f''(s+1)$$We obtained in the previous post that$$\displaystyle\lim_{s\to 1}\left(\zeta(s)-\frac{1}{s-1}\right)=\gamma$$Hence,$$\zeta(s)=\frac{1}{s-1}+\g-\g_1(s-1)+O((s-1)^2)$$where $\g_1$ denotes Stieltjes constant of order 1. And we see easily that$$2^s=1+s\ln2+s^2\frac{\ln^22}{2}+s^3\frac{\ln^22}{6}+O(s^4)$$$$\therefore\quad f(s+1)=\ln2+\left(\g\ln2-\frac{\ln^22}{2}\right)s+\left(-\g_1\ln2-\frac{\g\ln^22}{2}+\frac{\ln^32}{6}\right)s^2+O(s^3)$$Differentiate twice to get$$f''(s+1)=-2\g_1\ln2-\g\ln^22+\frac{\ln^32}{3}+O(s)\xrightarrow[]{s\to 0}-2\g_1\ln2-\g\ln^22+\frac{\ln^32}{3}$$
$$\sum_{n=1}^\infty\frac{(-1)^{n-1}H_n}{n^4} = \frac{59}{32}\zeta(5)-\frac{1}{2}\zeta(2)\zeta(3)$$$$\int_0^1\frac{\ln^2x\ln^2(1+x)}{x} = -\frac{29}{8}\zeta(5)+2\zeta(2)\zeta(3)$$PROOF here:
$$\int_0^x\frac{\ln^4 u}{1-u}du=24\Li_5(x)-24\Li_4(x)\ln x+12\Li_3(x)\ln^2x-4\ln^3x\Li_2(x)-\ln^4x\ln(1-x)$$(abbreviated) PROOF.$$LHS=\sum_{n=1}^\infty\int_0^x u^{n-1}\ln^4udu$$Integration by parts 4 times yields the equation.
Especially,$$\int_0^1\frac{\ln^4 u}{1-u}du=24\zeta(5)$$$$\int_0^\frac{1}{2}\frac{\ln^4 u}{1-u}du=24\Li_5\left(\frac{1}{2}\right)+24\Li_4\left(\frac{1}{2}\right)\ln 2+\frac{21}{2}\zeta(3)\ln^22-4\zeta(2)\ln^32+\ln^52$$
\begin{eqnarray*}\int_0^\frac{1}{2}\frac{\ln^4(1-u)}{u}du &=& 24\zeta(5)-24\Li_5\left(\frac{1}{2}\right)-24\Li_4\left(\frac{1}{2}\right)\ln 2\\&&\quad-\frac{21}{2}\zeta(3)\ln^22+4\zeta(2)\ln^32-\ln^52\\ \int_0^\frac{1}{2}\frac{\ln u\ln^3(1-u)}{1-u}du &=& 6\zeta(5)-6\Li_5\left(\frac{1}{2}\right)-6\Li_4\left(\frac{1}{2}\right)\ln 2\\&&\quad-\frac{21}{8}\zeta(3)\ln^22+\zeta(2)\ln^32\end{eqnarray*}(abbreviated proof)
The first integral can be obtained by putting $u\to 1-u$ and using the result of "2023/2/25". We easily find the second integral by IBP and using the first integral.
From @penta_math\begin{eqnarray*}\int_0^\infty\frac{\sqrt{x}}{x^3+1}dx &=& 2\int_0^1 \frac{\sqrt{x}}{x^3+1}dx \\&=& 2\sum_{n=0}^\infty(-1)^n\int_0^1 x^{3n+\frac{1}{2}}dx \\&=& \frac{2}{3}\sum_{n=0}^\infty\frac{(-1)^n}{n+\frac{1}{2}} \\&=& \frac{1}{3}\sum_{n=0}^\infty\left(\frac{1}{n+\frac{1}{4}}-\frac{1}{n+\frac{3}{4}}\right) \\&=&\frac{\psi(\frac{3}{4})-\psi(\frac{1}{4})}{3}\\&=& \frac{\pi}{3}\end{eqnarray*}
\begin{eqnarray*}&&\int_0^x\frac{\ln^2u\ln^2(1-u)}{u}du \\&=& -4\Li_5(x)+4\Li_4(1-x)\ln x-4\Li_4(x)\ln x-4\Li_4\left(\frac{x}{x-1}\right)\ln x\\&&+4\Li_3(x)\ln x\ln(1-x)-2\Li_3(1-x)\ln^2x\\&&+2\Li_2(1-x)\ln^2x\ln(1-x)+\ln^3x\ln^2(1-x)\\&&+\frac{2}{3}\ln^2x\ln^3(1-x)-\frac{1}{6}\ln x\ln^4(1-x)-2\zeta(2)\ln x\ln^2(1-x) \\&& +2\zeta(3)\ln^2x-4\zeta(4)\ln x-4\zeta(3)\ln x\ln(1-x)\\&&+4\sum_{n=1}^\infty\frac{H_n}{n^4}x^n\end{eqnarray*}
$$\int_0^1\frac{\ln^2u\ln^2(1-u)}{u}du = 8\zeta(5)-4\zeta(2)\zeta(3)$$\begin{eqnarray*}&&\int_0^\frac{1}{2}\frac{\ln^2u\ln^2(1-u)}{u}du \\&=& 4\Li_5\left(\frac{1}{2}\right)+\frac{1}{8}\zeta(5)+4\Li_4\left(\frac{1}{2}\right)\ln2+\frac{7}{4}\zeta(3)\ln^22\\&&-\frac{2}{3}\zeta(2)\ln^32-2\zeta(2)\zeta(3)-\frac{\ln^52}{15}\end{eqnarray*}
\begin{eqnarray*}&&\int_0^\frac{1}{2}\frac{\ln^2u\ln^2(1-u)}{1-u}du \\&=& -4\Li_5\left(\frac{1}{2}\right)+\frac{63}{8}\zeta(5)-4\Li_4\left(\frac{1}{2}\right)\ln2-\frac{7}{4}\zeta(3)\ln^22\\&&+\frac{2}{3}\zeta(2)\ln^32-2\zeta(2)\zeta(3)+\frac{\ln^52}{15}\end{eqnarray*}
\begin{eqnarray*}&&\int_0^1\frac{\ln^2x\ln^2(1+x)}{1+x} \\&=& 8\Li_5\left(\frac{1}{2}\right)-\frac{33}{8}\zeta(5)+8\Li_4\left(\frac{1}{2}\right)\ln2+\frac{7}{2}\zeta(3)\ln^22\\&&-\frac{4}{3}\zeta(2)\ln^32-2\zeta(2)\zeta(3)+\frac{4\ln^52}{15}\end{eqnarray*}
\begin{eqnarray*} \sum_{n=1}^\infty\frac{H_n}{n^42^n}&=& 2\Li_5\left(\frac{1}{2}\right)+\frac{1}{32}\zeta(5)+\Li_4\left(\frac{1}{2}\right)\ln2-\frac{\zeta(4)}{8}\ln2\\&&+\frac{\zeta(3)}{2}\ln^22-\frac{\zeta(2)}{6}\ln^32-\frac{1}{2}\zeta(2)\zeta(3)+\frac{\ln^52}{40}\end{eqnarray*}
PROOF:
NEXT:
Integrals and Miscellaneous 17
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。