Integrals and Miscellaneous 19

二重数列と二重級数（収束性と足し合わせの順）

正項の二重級数と和の順序

絶対収束する二重級数・和の順序、コーシー積

【１】無限積の定義と収束・発散

【２】無限積と級数の関係と収束性

【３】無限積の絶対収束と複素数の扱い

【４】条件収束する無限積の収束性（Cauchy's test）

【５】条件収束する無限積の収束性２（積の順序・Pringsheim's Test・regularly convergent）

$$\sqrt[3]{2+11i}+\sqrt[3]{2-11i}=4$$

Can we test the convergence of infinite products with the convergence of series ?$$P:=\prod_{n=1}^\infty (1+z_n)\quad ,\quad S:=\sum_{n=1}^\infty z_n$$then\begin{eqnarray*}P:\mathrm{absolutely\: convergent}&\Longleftrightarrow& S:\mathrm{absolutely\: convergent}\\P:\mathrm{conditionally\: convergent}&\nLeftrightarrow& S:\mathrm{conditionally\: convergent}\\P:\mathrm{divergent}&\nLeftrightarrow& S:\mathrm{divergent}\end{eqnarray*}

From @SrinivasR1729

$$S:=\sum_{n=0}^\infty\frac{(8n+1)!!}{(8n+2)!!(2n+1)(8n+1)}=\frac{2}{3}\left(\sqrt{2}-\sqrt{\sqrt{2}-1}\right)$$PROOF.\begin{eqnarray*}S &=& \frac{1}{2}\sum_{n=0}^\infty \frac{(\frac{1}{8})_n(\frac{3}{8})_n(\frac{5}{8})_n(\frac{7}{8})_n}{(\frac{3}{4})_n(\frac{5}{4})_n(\frac{3}{2})_n n!} \\&=&\frac{1}{2}{}_4F_3\left[\begin{matrix}\frac{1}{8},\frac{3}{8},\frac{5}{8},\frac{7}{8}\\\frac{3}{4},\frac{5}{4},\frac{3}{2}\end{matrix};1\right]\end{eqnarray*}Exton[1] deduced (and Brychkov[2] corrected) that$${}_4F_3\left[\begin{matrix}\frac{a+1}{2},\frac{a}{2}+1,\frac{b+1}{2},\frac{b}{2}+1\\\frac{a-b}{2}+1,\frac{a-b+3}{2},\frac{3}{2}\end{matrix};1\right]=\frac{1}{2ab}\left(\frac{\G(2+a-b)\G(1-2b)}{\G(1-b)\G(1+a-2b)}-\frac{\G(2+a-b)\G(1+\frac{a}{2}}{\G(1+a)\G(1+\frac{a}{2}-b)}\right)$$where $\mathfrak{R}b<\frac{1}{2}$. Substituting $a=-\frac{3}{4}$ , $b=-\frac{1}{4}$ yields$${}_4F_3\left[\begin{matrix}\frac{1}{8},\frac{3}{8},\frac{5}{8},\frac{7}{8}\\\frac{3}{4},\frac{5}{4},\frac{3}{2}\end{matrix};1\right]=\frac{4}{3}\left(\sqrt{2}-\sqrt{\sqrt{2}-1}\right)$$Hence,$$\sum_{n=0}^\infty\frac{(8n+1)!!}{(8n+2)!!(2n+1)(8n+1)}=\frac{2}{3}\left(\sqrt{2}-\sqrt{\sqrt{2}-1}\right)$$

[1] H.Exton(1997), Some new summation formulae for the generalised hypergeometric function of higher order
[2] Yury Brychkov, Handbook of Special Functions: Derivatives, Integrals, Series and Other Formulas

From @6ahRJ6PeIkQWmsk$$I:=\int_0^\infty\frac{\sin x\ln x}{x}dx=-\frac{\g\pi}{2}$$PROOF.$$f(z):=\frac{e^{iz}\ln z}{z}$$We consider the $z$-plane whose negative imaginary axis is the brunch cut ($-\frac{\pi}{2}<\arg z<\frac{3}{2}\pi$).

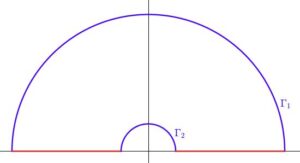
There is no singularity in the above contour then\begin{eqnarray*}0 &=& \int_\infty^\epsilon\frac{e^{-ix}(\ln x+i\pi)}{-x}(-dx)+ \int_\pi^0 e^{i\epsilon e^{i\t}}(\ln\epsilon+i\t) id\t \\&&+\int_\epsilon^\infty\frac{e^{ix}\ln x}{x}dx+\int_0^\pi e^{iRe^{i\t}}(\ln R+i\t )id\t\\&=& 2i\: I-i\pi\int_\epsilon^\infty\frac{e^{-ix}}{x}dx -i\int_0^\pi e^{i\epsilon e^{i\t}}(\ln\epsilon+i\t) d\t +i\int_0^\pi e^{iRe^{i\t}}(\ln R+i\t )d\t\\&=& 2i\: I-i\pi\left(-\mathrm{Ci}(\epsilon)-i\frac{\pi}{2}\right) -i\pi\ln\epsilon+\frac{\pi^2}{2} +i\int_0^\pi e^{iRe^{i\t}}(\ln R+i\t )d\t\\&=&2i\: I+i\pi\mathrm{Ci}(\epsilon)-i\pi\ln\epsilon+i\int_0^\pi e^{iRe^{i\t}}(\ln R+i\t )d\t\end{eqnarray*}The last term is\begin{eqnarray*}\left|\int_0^\pi e^{iRe^{i\t}}(\ln R+i\t )d\t\right| &\le&\int_0^\pi e^{-R\sin\t}(\ln R+\t)d\t \le(\ln R+\pi)\int_0^\pi e^{-R\sin\t}d\t \\&=& \frac{\ln R+\pi}{2}\int_0^\frac{\pi}{2} e^{-R\sin\t}d\t \le\frac{\ln R+\pi}{2}\int_0^\frac{\pi}{2} e^{-\frac{2R}{\pi}\t}d\t \\&=&\frac{\ln R+\pi}{2}\frac{\pi}{2R}(1-e^{-R}) \rightarrow 0\end{eqnarray*}From $\mathrm{Ci}(x)=\g+\ln x +O(x^2)$ it follows that$$\int_0^\infty\frac{\sin x\ln x}{x}dx=-\frac{\g\pi}{2}$$REFERENCE:
Abramowitz, M., Stegun, I. A. (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover. 【楽天はココ】

From @nasya_tw $$I:=\int_0^{3^{-1/3}}\frac{dx}{(1-x^6)^\frac{2}{3}}=\frac{\G^3(\frac{1}{3})}{2^\frac{7}{3}\sqrt{3}\pi}$$PROOF.\begin{eqnarray*}I &=& \int_0^{3^{-1/3}}\sum_{n=0}^\infty\frac{(\frac{2}{3})_n}{n!}x^{6n}dx\\&=&\frac{1}{3^{1/3}}\sum_{n=0}^\infty \frac{(\frac{2}{3})_n}{n!(6n+1)9^n}\\&=&\frac{1}{3^{1/3}} F\left[\begin{matrix}\frac{2}{3},\frac{1}{6}\\\frac{7}{6}\end{matrix};\frac{1}{9}\right]\end{eqnarray*}Recall the formula$$F\left[\begin{matrix}2s,\frac{1}{2}-s\\s+\frac{5}{6}\end{matrix};\frac{1}{9}\right]=\frac{3^{s}\G(s+\frac{5}{6})\G(\frac{2}{3})}{4^{s}\G(s+\frac{2}{3})\G(\frac{5}{6})}$$ which we deduced here. Setting $s=1/3$ yields$$I=\frac{\G^3(\frac{1}{3})}{2^\frac{7}{3}\sqrt{3}\pi}$$

\begin{eqnarray}\sum_{n=1}^\infty\frac{H_n^2}{n(n+1)}x^n &=& \Li_3(x)-\frac{2\Li_3(1-x)}{x}+\left(\frac{1}{x}-1\right)\ln(1-x)\Li_2(x)+\left(\frac{1}{x}-1\right)\frac{\ln^3(1-x)}{3}\\&&+\frac{2}{x}\ln(1-x)\Li_2(1-x)+\frac{\ln x\ln^2(1-x)}{x}+\frac{2\zeta(3)}{x}\end{eqnarray}$$\sum_{n=1}^\infty\frac{H_n^2}{n(n+1)2^n}=\frac{11}{8}\zeta(3)-\frac{\pi^2}{6}\ln 2-\frac{\ln^32}{3}$$$$\sum_{n=1}^\infty\frac{H_n^2}{n(n+1)}=3\zeta(3)$$

調和数を含んだ級数とゼータ関数 part3

【７】関数列の無限積における具体例（ヴィエトの公式・ゼータ関数）

【８】整関数とワイエルシュトラスの因数分解定理①（基本乗積・種数）

【９】整関数とワイエルシュトラスの因数分解定理②（完全版）

$$f(z)=z^m e^{g(z)}\prod_{n=1}^\infty \left(1-\frac{z}{\lambda_n}\right)e^{\frac{z}{\lambda_n}+\frac{z^2}{2\lambda_n^{~2}}+\cdots\frac{z^{k_n}}{k_n\lambda_n^{~k_n}}}$$

$$\sum_{n=1}^\infty\frac{(a)_n}{n!}H_nx^n=-(1-x)^{-a}\ln\frac{1-x}{x}+\{\psi(a)+\g\}(1-x)^{-a}+\frac{1}{a}F\left[\begin{matrix}1,a\\1+a\end{matrix};1-x\right]$$$$\therefore\quad \sum_{n=0}^\infty\frac{(\frac{1}{2})_n}{n!}H_nx^n=\frac{2}{\sqrt{1-x}}\ln\frac{1+\sqrt{1-x}}{2\sqrt{1-x}}$$$$\sum_{n=0}^\infty\frac{(\frac{1}{2})_n}{n!}(2H_{2n}-H_n)x^{n}=-\frac{\ln(1-x)}{\sqrt{1-x}}$$

超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値１

調和数と超幾何級数3

$$f(z)=g(z)\left(\frac{z}{R}\right)^m\prod_{n=1}^\infty \frac{|a_n|}{a_n}\frac{R(z-a_n)}{\bar{a_n}z-R^2}$$

【10】開円板上の正則関数とBlaschke積

$$\int_a^{a+1}\ln\G(x)dx=a\ln a-a+\frac{\ln2\pi}{2}$$

【γ20】ガンマ関数の漸近展開（ビネの第2公式・arctanの展開・スターリング級数）（ガンマ関数の基礎20）

Brafman's generating functions$${}_2F_1\left[\begin{matrix}c,1-c\\1\end{matrix};\frac{1-t-\rho}{2}\right]{}_2F_1\left[\begin{matrix}c,1-c\\1\end{matrix};\frac{1+t-\rho}{2}\right]=\sum_{n=0}^\infty\frac{(c)_n(1-c)_nP_n(x)}{n!^2}t^n$$where $\rho=(1-2xt+t^2)^{1/2}$.

[1] Brafman, F. (1951). Generating functions of Jacobi and related polynomials. Proceedings of the American Mathematical Society, 2(6), 942–949.
[2] Rainville, E.D. (1960) Special Functions. The Macmillan Company, New York.

Machin's formula$$\frac{\pi}{4}=4\arctan\left(\frac{1}{5}\right)-\arctan\left(\frac{1}{239}\right)$$Euler's formula$$\frac{\pi}{4}=\arctan\left(\frac{1}{2}\right)+\arctan\left(\frac{1}{3}\right)$$Hermann's formula$$\frac{\pi}{4}=2\arctan\left(\frac{1}{2}\right)-\arctan\left(\frac{1}{7}\right)$$Hutton's formula$$\frac{\pi}{4}=2\arctan\left(\frac{1}{3}\right)+\arctan\left(\frac{1}{7}\right)$$Euler's formula$$\pi=20\arctan\left(\frac{1}{7}\right)+8\arctan\left(\frac{3}{79}\right)$$Dase's formula(?)$$\frac{\pi}{4}=\arctan\left(\frac{1}{2}\right)+\arctan\left(\frac{1}{5}\right)+\arctan\left(\frac{1}{8}\right)$$Ferguson's formula(?)$$\frac{\pi}{4}=3\arctan\left(\frac{1}{4}\right)+\arctan\left(\frac{1}{20}\right)+\arctan\left(\frac{1}{1985}\right)$$Shanks-Wrench(?)$$\pi=24\arctan\left(\frac{1}{8}\right)+8\arctan\left(\frac{1}{57}\right)+4\arctan\left(\frac{1}{239}\right)$$

[1] Borwein & Borwein, Pi and the AGM, 340-345p