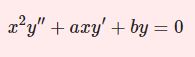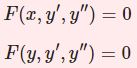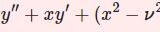ベッセルの微分方程式を少し変形した微分方程式を考える．この特殊解は変形ベッセル関数とよばれ，ベッセル関数とよく似た性質を持つ．
\begin{equation}x^2y^{\prime\prime}+xy'-(x^2+\nu^2)y=0 \quad (\nu \in \mathbb{R})\tag{1}\end{equation}
「ベッセルの微分方程式」と1か所だけ符号が異なる方程式です．ベッセルの微分方程式については以下を参照ください．
【D18】ベッセルの微分方程式と級数解
ふつうのベッセルの微分方程式は$$x^2y^{\prime\prime}+xy'+(x^2-\nu^2)y=0 \quad (\nu \in \mathbb{R})$$と表されます．一般解は２つの特殊解の線型結合であり$$y(x)=c_1J_\nu(x)+c_2Y_\nu(x)$$となります．ここで $J_\nu$ を第1種ベッセル関数，$Y_\nu$ を第2種ベッセル関数とよびます．これらは以下の表式で与えられます．\begin{equation}J_\nu(x) = \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m+\nu}\tag{2}\end{equation}$$\begin{cases}Y_\nu(x)=\displaystyle\frac{1}{\sin\nu\pi}[J_\nu(x)\cos\nu\pi-J_{-\nu}(x)]\\[1em]Y_n(x)=\displaystyle\lim_{\nu\to n}Y_\nu(x)\quad(n\in\mathbb{Z})\end{cases}$$
ベッセルの微分方程式の解がベッセル関数であることは，$x$ が複素数であっても変わりありません．つまり$$z^2\frac{d^2y}{dz^2}+z\frac{dy}{dz}+(z^2-\nu^2)y=0$$の特殊解はやはり $J_\nu(z)$ であるということです．
純虚数 $z=ix$ とおくと $J_\nu(ix)$ が解となる方程式は次のようになります．\begin{eqnarray*}&&(ix)^2\frac{d^2y}{d(ix)^2}+ix\frac{dy}{d(ix)}+((ix)^2-\nu^2)y=0\\&\Leftrightarrow&x^2\frac{d^2y}{dx^2}+x\frac{dy}{dx}-(x^2+\nu^2)y=0\end{eqnarray*}すなわち変形ベッセル方程式(1)の特殊解は $J_\nu(ix)$ であることが分かります．これが実数となるように定数倍した$$I_\nu(x)\equiv i^{-\nu}J_\nu(ix)$$を第1種変形ベッセル関数といいます．
(2)を用いて第1種変形ベッセル関数を明示的に表すと\begin{eqnarray*}I_\nu(x)&=&i^{-\nu}J_\nu(ix)\\&=& i^{-\nu}\sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m! \Gamma(m+\nu+1)}(ix)^{2m+\nu}\\&=& \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m! \Gamma(m+\nu+1)}(-1)^mx^{2m+\nu}\\&=& \sum^\infty_{m=0}\frac{1}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m+\nu}\end{eqnarray*}と確かに実数値となっています．
ベッセル関数のときと同様，$\nu$ が非整数であれば $I_\nu$ と $I_{-\nu}$ は独立なので一般解を与えます．しかし $\nu$ が整数 $n$ のときは\begin{eqnarray*}I_{-n}(x)&=&i^{n}J_{-n}(ix)= i^{n}(-1)^nJ_{n}(ix)\\&=&i^{-n}J_{n}(ix)=I_n(x)\end{eqnarray*}よって $I_{-n}(x)=I_n(x)$ ですから一次従属となって一般解がつくれません．
そこでいかなるときも $I_\nu$ と独立な特殊解である第2種変形ベッセル関数 $K_\nu$を導入します．第2種変形ベッセル関数は$$K_\nu(x)=\frac{\pi}{2\sin\nu\pi}[I_{-\nu}(x)-I_\nu(x)]$$と定義されます．$\nu$ が整数のときは分母がゼロになってしまうので $\nu\to n$ の極限をとります．
$\nu=n$ のときの $K_n(x)$ を明示的に書き下すと以下のようになります．\begin{eqnarray*}K_n(x)=&&(-1)^{n+1} \left(\gamma+\log\frac{x}{2}\right)\sum^\infty_{m=0}\frac{1}{2^{2m+n}m!(m+n)!}x^{2m+n}\\ &+& \frac{(-1)^n}{2}\sum^\infty_{k=0}\frac{(\frac{x}{2})^{n+2k}}{k!(n+k)!}\left(\sum_{m=1}^k\frac{1}{m}+\sum_{m=1}^{k+n}\frac{1}{m} \right)\\ &+& \frac{1}{2}\sum_{r=0}^{n-1}(-1)^r\frac{(n-r-1)!}{r!2^{2r-n}}x^{2r-n}\end{eqnarray*}
以上より
変形ベッセル方程式$$x^2y^{\prime\prime}+xy'-(x^2+\nu^2)y=0 \quad (\nu \in \mathbb{R})$$の一般解は第1種変形ベッセル関数 $I_\nu$ と第2種変形ベッセル関数 $K_\nu$ を用いて$$y(x)=c_1I_\nu(x)+c_2K_\nu(x)$$
$I_\nu$ や $K_\nu$ は一般に初等関数であらわせない特殊関数ですが，$\nu$ が半整数のときは初等関数となります．
\begin{eqnarray*}I_{\frac{1}{2}}(x)&=& x^{\frac{1}{2}}\sum^\infty_{m=0}\frac{1}{2^{2m+\frac{1}{2}}m! \Gamma(m+\frac{3}{2})}x^{2m}\\&=& \sqrt{\frac{2}{x}}\sum^\infty_{m=0}\frac{x^{2m+1}}{2^{2m+1}m! \Gamma(m+\frac{3}{2})}\\&=& \sqrt{\frac{2}{x}}\sum^\infty_{m=0}\frac{x^{2m+1}}{2^{2m+1}m!(m+\frac{1}{2})(m-\frac{1}{2})\cdots\frac{3}{2}\frac{1}{2}\sqrt{\pi}}\\&=& \sqrt{\frac{2}{\pi x}}\sum^\infty_{m=0}\frac{x^{2m+1}}{(2m)!!(2m+1)!!} \\&=& \sqrt{\frac{2}{\pi x}}\sum^\infty_{m=0}\frac{x^{2m+1}}{(2m+1)!} \\&=& \sqrt{\frac{2}{\pi x}}\sinh x\end{eqnarray*}
同じように$$I_{-\frac{1}{2}}(x)=\sqrt{\frac{2}{\pi x}}\cosh x$$が成立します．次に第2種のほうは\begin{eqnarray*}K_{\frac{1}{2}}(x)&=&\frac{\pi}{2\sin\frac{\pi}{2}}[I_{-1/2}(x)-I_{1/2}(x)]\\&=&\frac{\pi}{2}\sqrt{\frac{2}{\pi x}}(\cosh x-\sinh x)\\&=&\sqrt{\frac{\pi}{2x}}e^{-x}\end{eqnarray*}よって $\nu=1/2$ の変形ベッセル関数は初等関数であることが示されました．
ここで漸化式を導出します．\begin{eqnarray*}(x^\nu I_\nu)' &=& \sum^\infty_{m=0}\frac{(2m+2\nu)x^{2m+2\nu-1}}{2^{2m+\nu}m! \Gamma(m+\nu+1)}\\&=&x^\nu\sum^\infty_{m=0}\frac{x^{2m+\nu-1}}{2^{2m+\nu-1}m! \Gamma(m+\nu)}\\&=& x^\nu I_{\nu-1}\end{eqnarray*}\begin{eqnarray*}(x^{-\nu} I_\nu)' &=&\sum^\infty_{m=1}\frac{2mx^{2m-1}}{2^{2m+\nu}m! \Gamma(m+\nu+1)}\\&=& \sum^\infty_{m=1}\frac{x^{2m-1}}{2^{2m+\nu-1}(m-1)! \Gamma(m+\nu+1)}\\&=& \sum^\infty_{m=0}\frac{x^{2m+1}}{2^{2m+\nu+1}m! \Gamma(m+\nu+2)}\\&=& x^{-\nu}\sum^\infty_{m=0}\frac{x^{2m+\nu+1}}{2^{2m+\nu+1}m! \Gamma(m+\nu+2)}\\&=& x^{-\nu}I_{\nu+1}\end{eqnarray*}これらの微分を実行することで以下の式を得ます．$$\begin{cases}\nu x^{\nu-1}I_\nu+x^\nu I'_\nu&=&x^\nu I_{\nu-1}\\ -\nu x^{-\nu-1}I_\nu+x^{-\nu}I'_\nu&=& -x^{-\nu}I_{\nu+1}\end{cases}$$これより $I'_\nu$ を消去すると$$I_{\nu+1}+I_{\nu-1}=\frac{2\nu}{x}I_\nu$$
この漸化式および，$\nu=\pm 1/2$ で $I_\nu$ が初等関数であることから，$\nu$ があらゆる半整数のときに $I_\nu$ が初等関数となることが分かります．また $K_\nu$ もその定義から初等関数と分かります．
次の記事：
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
常微分方程式シリーズ
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
