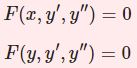２階線型微分方程式の一般解は２つの独立な特殊解の線型結合である。ここでは斉次の場合の基本的な解法を示す。1つ目は「特殊解」が１つ分かっているときにもう１つを求める方法。２つ目は定数係数の方程式の解法である。なお、級数法などは解説が重たいので別記事に譲る。
微分方程式の基本的な考え方については、まず１階の方程式の記事を参照ください。
【D1】１階線型微分方程式の解法
2階線型微分方程式は以下のように書ける方程式です。
$$y^{\prime\prime}+p(x)y' +q(x)y=\begin{cases} 0 &(斉次 \textrm{Homogeneous)} \\ r(x) &(非斉次 \textrm{Nonhomogeneous})\end{cases}$$今回は斉次方程式の解き方を見ていきますので、考えるべき方程式は
$$y^{\prime\prime}+p(x)y' +q(x)y=0$$
解法は係数によって本当に様々です。1階に比べるとものすごく複雑です。そのなかで解 $y_1 , y_2$ が見つかったとしましよう。これを特殊解といいます。2階の方程式では、まず特殊解を2つ見つける必要があるのです。特殊解を線型結合すると$$y=c_1y_1+c_2y_2$$となり、これを一般解といいます。一般解は微分方程式の解をすべて見つけたことの証であり、「微分方程式を解く」というのは一般解を導き出すということになります。
特殊解 $y_1,y_2$が見つかると$$y_1^{\prime\prime}+p(x)y_1' +q(x)y_1=0\quad , \quad y_2^{\prime\prime}+p(x)y_2' +q(x)y_2=0$$が成り立ちます。ここで $y=c_1y_1+c_2y_2$ をもとの微分方程式に代入するとこの $y$ もちゃんと解になっていることが確認できます。
もちろん２つの特殊解は独立である必要があります。例えば $e^x$ と $2e^x$ は独立ではありません。これらを線型結合しても $$c_1e^x+c_2 2e^x=(c_1+2c_2)e^x$$となって定数を改めれば $ce^x$ となってしまいます。これではダメでなのです。
方程式 $y^{\prime\prime}+p(x)y' +q(x)y=0$ において、１つだけ特殊解が分かっているが、２つ目の特殊解が見つからない場合、階数低減法を使って解きます（階数低減法と名前の付く解法はほかにいろいろあるらしいですが）。
$y_1$ が $x$ の関数として分かっている場合 $y_2=y_1u(x)$ とおいてもとの微分方程式に代入するというものです。これでなぜうまくいくのか考えてみます。
まず解 $y_1$ は当然 $$y_1^{\prime\prime}+p(x)y'_1+q(x)y_1=0$$を満たします。ここで方程式に $y_2=y_1u(x)$ を代入します。\begin{eqnarray*}左辺&=& y_2^{\prime\prime}+p(x)y'_2 +q(x)y_2\\ &=& (y_1u)^{\prime\prime}+p(y_1u)'+q(y_1u)\\ &=& u(y_1^{\prime\prime}+py'_1+qy_1)+y_1u^{\prime\prime}+(2y_1+py_1)u'\\ &=& y_1u^{\prime\prime}+(2y'_1+py_1)u' \\&=& 0\end{eqnarray*}最後の2行は $u'$ に関する1階の微分方程式になっています。$u$ が求まれば $y_2$ も求まり、２つの特殊解から一般解を得ておしまいです。
例題：階数低減法
$x^2y^ {\prime\prime} -xy'+y=0 $ を解け。なお $y_1=x$ は解であることをまず確かめよ。
冒頭とは少し方程式の形が違うようですが、両辺を $x^2$ で割ればこれまで説明してきた形になります。まず指示通り $y_1=x$ を代入すると、これは確かに解であることが分かります。では残りの特殊解を見つけましょう。
$y_2=xu(x)$ とすると$${y_2}'=xu'+u\;,\;y^{\prime\prime}_2=xu^{\prime\prime}+2u'$$となりますので、もとの方程式に代入すると$$x^2(xu^{\prime\prime} +2u')-x(xu'+u)+xu=0$$$$\therefore\quad xu^{\prime\prime}+u'=0$$を得ます。
これは $u'$ についての1階微分方程式ですが、見やすいように $u'=z(x)$ とおくと $xz'+z=0$ と書き直せます。変数分離で $z$ は簡単に解けて$$u'=z=\frac{c_1}{x}$$となります。したがって$$u=c_1\log x+c_2$$$$\therefore\quad y_2=c_1x\log x+c_2x$$一般解は $y_1$ と $y_2$ の重ね合わせですが、$y_2$の中に $y_1$ がすでに含まれていますので、$y_2$ をそのまま一般解としてよいです（ピンとこない場合は、実際に線型結合してみると分かると思います）。
最終的に$$y(x)=c_1x\log x+c_2x$$
ちなみにこの問題は「オイラー・コーシーの方程式」というタイプで、特殊解２つを自力で見つけることができます。試行解 $y_1=x^r$ を代入すると $r=1$ となるのです。
$xy^{\prime\prime}+2y'+xy=0$ を解け。なお $y_1=\displaystyle\frac{\sin x}{x}$ は解であることをまず確かめよ。
$y_2=\displaystyle\frac{\sin x}{x}u(x)$ として方程式に代入すると$$u^{\prime\prime}\sin x+2u'\cos x=0$$となります。$u'=z$ とおいて$$z'\sin x+2z\cos x=0$$変数分離により$$\frac{dz}{z}=-2\frac{\cos x dx}{\sin x}$$積分して$$z=\frac{c}{\sin^2x}$$さらに積分して$$u=-c_1\frac{\cos x}{\sin x}+c_2$$となります。よって$$y_2=-c_1\frac{\cos x}{x}+c_2\frac{\sin x}{x}$$ですが、これは $y_1$ を含んでいるのでこのまま一般解です。$-c_1$ を $+c_1$ と置き換えるとよりきれいです。
最終的に$$ y(x)=c_1\frac{\cos x}{x}+c_2\frac{\sin x}{x}$$
ちなみに $y_1$ が分かっていない場合、まず方程式を $x$ で割って第2項の係数 $2/x$ を用いて
$$y=u(x)\exp\left(-\int\frac{2/x}{2}dx\right)$$とおくと解けます。
次に係数が定数の場合つまり
$$y^{\prime\prime}+py' +qy=0$$
なる方程式の解法を見ていきます。 2つの特殊解を見つけ、一般解を示すのがゴールです。
試しに方程式に代入する解を「試行解」といいます。解の形がだいたい分かっているときやパターン化されているときに有効です。定数係数での解法は確立されていて、代入すべき試行解も決まっています。
試行解 $y=e^{\lambda x}$ を代入します。$\lambda$ は複素数です。もとの方程式を成立させるような $\lambda$ があれば、この試行解は「あたり」なわけです。実際に代入すると$$\lambda^2e^{\lambda x}+p\lambda e^{\lambda x}+qe^{\lambda x}=0$$$$\therefore\quad \lambda^2+p\lambda+q=0$$つまり $\lambda$ は二次方程式 $X^2+pX+q=0$ の2解として現れるということになります。この解を $\lambda_1,\lambda_2$ とすれば特殊解は $e^{\lambda_1 x},e^{\lambda_2 x}$ ですので一般解$$y=c_1e^{\lambda_1 x}+c_2e^{\lambda_2 x}$$を得ます。
微分方程式 $y''-6y'+8y=0$ に $y=e^{2x}$ および $y=e^{4x}$ を代入し，この２つが確かに解であることを確かめよ．
重解となってしまう場合
試行解を代入した結果 $\lambda$ が重解となるために解が１つしか得られない場合、別の方法でもう１つの解を探す必要があります。
先ほど特殊解が１つ分かっている場合にもう１つの解を求める方法を解説しました。それを利用するのです。
微分方程式$$y^{\prime\prime}-2ay'+a^2y=0$$に試行解を代入すると特殊解 $e^{ax}$ のみを得ます。ここでもう１つの特殊解を $y=e^{ax}u(x)$ とおくのです。これを代入すると$$(u^{\prime\prime}+2au'+a^2u)e^{ax}-2a(u'+au)e^{ax}+a^2ue^{ax}=0$$
これを整理すると $u^{\prime\prime}=0$ です。すなわち $u=Ax+B$ であり、求める特殊解は $y=(Ax+B)e^{ax}$ としたいところです。でもよくみると定数 $B$ の項 $Be^{ax}$ は始め得た特殊解の実数倍なので不要です。結局ほしい特殊解は $y=xe^{ax}$ となります。従って一般解は$$y=c_1e^{ax}+c_2xe^{ax}$$となります。
$y^{\prime\prime}-3y'+2y=0 $ を解け．
$y=e^{\lambda x}$ を代入し$$\lambda^2-3\lambda +2=0$$よって $\lambda=1,2$ なので一般解は$$y=c_1e^{x}+c_2e^{2x}$$
$y^{\prime\prime}+8y'+16y=0$ を解け．
$y=e^{\lambda x}$ を代入し、$$\lambda^2+8\lambda +16=0$$よって重解 $\lambda =-4$ を得ます。よって一般解は$$y=c_1e^{-4x}+c_2xe^{-4x}$$
$y^{\prime\prime}-2y'+2y=0$ を解け．
$y=e^{\lambda x}$ を代入し$$\lambda^2-2\lambda +2=0$$よって $\lambda=1\pm i$ を得ます。したがって一般解は\begin{eqnarray*}y &=& c_1e^{(1+i)x}+c_2e^{(1-i)x}\\ &=& c_1e^xe^{ix}+c_2e^xe^{-ix}\\ &=& c_1e^x(\cos x+i\sin x)+c_2e^x(\cos x-i\sin x)\\ &=& (c_1+c_2)e^x\cos x+(ic_1-ic_2)e^x\sin x \\ &=& e^x(A\cos x+B\sin x)\end{eqnarray*}
と求まります。最後、定数は置き換えました。
これはまた別の定数で $$y=Ce^x\sin(x+\phi)$$とすることもできます。
$y^{\prime\prime}+y=0$ を解け．
$y=e^{\lambda x}$ を代入し$$\lambda^2+1=0$$よって $\lambda=\pm i$ を得ます。したがって一般解は\begin{equation}y = c_1e^{ix}+c_2e^{-ix}\tag{1}\end{equation}あるいは定数を$$c_1=\frac{A+B}{2}\quad,\quad c_2=\frac{A-B}{2}$$と置きなおせば\begin{equation}y=A\cos x+B\sin x\tag{2}\end{equation}(1)と(2)が同じであるというのは面白いですね。数式は見た目によらないってことです。
たかが定数係数の方程式と思っても、以上の４題を見るとそれぞれ解の形が違っていて割と奥が深い気がします。このタイプの方程式は力学や交流回路の方程式にも頻出するので、実践的な話でまた扱いたいです。
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
