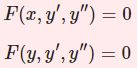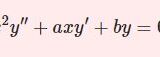2階微分方程式のうち $y$ が含まれていないバージョン $F(x,y',y^{\prime\prime})=0$ および $x$ が含まれないもの $F(y,y',y^{\prime\prime})=0$ を階数低減法によって解く方法を解説する。非斉次や非線型のものも含まれる。
前回記事
【D5】斉次2階線型微分方程式
一般に2階微分方程式は2階微分までの項を含みますので $F(x,y,y',y^{\prime\prime})=0$ と表せます。今回は2階微分方程式のうち $y$ または $x$ が含まれていないバージョンについて見ていきます。
$$F(x,y',y^{\prime\prime})=0 $$$$ F(y,y',y^{\prime\prime})=0 $$
$ F(x,y',y^{\prime\prime})=0 $ は非常に単純です。$y'$ からしてみれば $y''$ は1階微分です。すなわち $y'=u(x)$ と置けば $F(x,u,u')=0$ となり、1階の微分方程式に帰着します。よって1種の「階数低減法」といえるでしょう。
$2xy^{\prime\prime}-3y'=0 $ を解け．
$y'=u(x)$ として$$2xu'-3u=0$$となります。これは変数分離して$$\frac{du}{u}=\frac{3dx}{2x}$$を積分することで$$u(x)=\log cx^{3/2}$$を得ます。$y'=u$ ですから $y$ を得るにはさらに $u$ を積分し$$y=\frac{2}{5}cx^{5/2}+c_2$$です。$c$ を書き改めて$$y=c_1x^{5/2}+c_2$$でOKです。
重力 $mg$ および空気抵抗 $kv(<mg)$ を受けて鉛直下向きに落下する物体の運動方程式$$m\frac{d^2x}{dt^2}=mg-k\frac{dx}{dt}$$を解け．ただし初期条件は $x(0)=x'(0)=0$ とする．
$x$ は座標です。その時間微分は速度なので $x'=v$ とおくと$$\frac{dv}{dt}=g-\frac{k}{m}v$$変数分離によって$$dt=\frac{dv}{g-\frac{k}{m}v}$$積分して初期条件 $x'(0)=v(0)=0$ を取り入れれば$$t=-\frac{m}{k}\log(1-\frac{kv}{mg})$$$$\therefore \quad v(t)=\frac{mg}{k}(1-e^{-\frac{k}{m}t})$$時刻 $t$ を大きくしていけば速度 $v$ は$mg/k$ へ収束していきます（終端速度）。
さらに積分して初期条件 $x(0)=0$ を取り入れれば$$x(t)=\frac{mg}{k}\left[t-\frac{m}{k}(1-e^{-\frac{k}{m}t})\right]$$となり、時刻 $t$ における座標 $x$ が求まりました。
このように物理でもよく出てきますね。
次に $F(y,y',y^{\prime\prime})=0$ について見ていきます。$y$ はもちろん $x$ の関数ですが、方程式の中に $x$ があらわには含まれていません（こういうのを「陽に含まれない」といいます）。
こいつの解法はずばり「$y$ を独立変数とみる」です。
2階微分方程式 \begin{equation}F(y,y',y^{\prime\prime})=0\tag{1}\end{equation}において $x$ がないのをいいことに $y$ を独立変数とみなします。さらに $z\equiv y'$ とします。すると2階微分の項は$$y^{\prime\prime}=\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}=\frac{dz}{dy}y'=z\frac{dz}{dy}$$となって微分方程式(1)は結局 $$F\left( y, z,z\frac{dz}{dy}\right)=0$$ となります。これは $z$ を $y$ の関数 $z(y)$ とみた1階微分方程式です。なのでやはり一種の階数低減法ですね。これを解いて $z=(yの式)$ となれば結局 $y'=(yの式)$ となり、もう一度1階微分方程式を解くという格好になります。
$yy^{\prime\prime}=2y'^2$ を解け．
この式には $x$ が含まれていません。早速 $y'=z$ とおき$$y^{\prime\prime}=z\frac{dz}{dy}$$とおきかえれば$$yz\frac{dz}{dy}=2z^2$$変数分離をめざして整理すると$$2\frac{dy}{y}=\frac{dz}{z}$$積分して$$z=cy^2 \Longleftrightarrow y'=cy^2$$となります。これもまた典型的な変数分離法で$$\frac{dy}{y^2}=cdx$$$$\therefore\quad \frac{1}{y}=-(cx+c')$$負符号は定数に押し付けて結局$$y=\frac{1}{c_1x+c_2}$$と解けました。
$y^{\prime\prime}+e^yy'^3=0$ を解け．初期条件を $y(0)=0\; ,\; y'(0)＝1$ とする．
$y'=z$ および $y^{\prime\prime}=z\frac{dz}{dy}$ を代入して$$z\frac{dz}{dy}+e^yz^3=0$$変数分離法を目指して変形します。$$\frac{dz}{z^2}=-e^ydy$$積分して$$z=\frac{1}{e^y+c}=y'$$$y(0)=0\; ,\; y'(0)＝1$ の初期条件を適用すると $c=0$ です。変数分離してさらに積分すると$$e^y+C=x$$初期条件から $e^y-1=x$ なので最終的に$$y=\log (x+1)$$
$y^{\prime\prime}(y+1)=1+y'^2$ を解け．初期条件 $y(0)=0$ , $y'(0)=1$ とする．
過去に光の屈折と変分法について扱った記事から再掲です。当該記事は
変分法と光の屈折（フェルマーの原理を起点に）
をご覧ください。
$y'=u(y)$ とおきます。すると2階微分は$$y^{\prime\prime}=\frac{du(y)}{dx}=\frac{dy}{dx}\frac{du}{dy}=u\frac{du}{dy}$$微分方程式に代入して$$u\frac{du}{dy}(y+1)=1+u^2\Longrightarrow \frac{udu}{1+u^2}=\frac{dy}{y+1}$$変数分離ですね。両辺を積分して$$\log\sqrt{1+u^2}=\log(y+1)+C$$初期条件 $y(0)=0$ と $y'(0)=u(0)=1$ によって$$C=\frac{1}{2}\log2$$よって$$\log\sqrt{1+u^2}=\log\sqrt{2}(y+1)$$$u=y'$ に注意して変形をほどこすと$$\frac{dy}{dx}=\sqrt{2(y+1)^2-1} $$変数分離法によって$$\sqrt{2}x=\textrm{arccosh}\sqrt{2}(y+1)-\log(\sqrt{2}+1)$$移項して$$\textrm{arccosh}\sqrt{2}(y+1)=\sqrt{2}x+\log(\sqrt{2}+1)$$となって$$\cosh(\sqrt{2}x+\log(\sqrt{2}+1))=\sqrt{2}(y+1)$$のように変形できます。最後は $\cosh$ の定義に従って計算して$$y(x)=\cosh\sqrt{2}x+\frac{1}{\sqrt{2}}\sinh\sqrt{2}x-1$$
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
