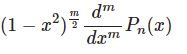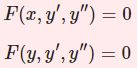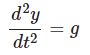「ルジャンドルの陪微分方程式」の特殊解の求め方を，前回の「ルジャンドル多項式」との関連で解説する。またその特殊解「ルジャンドル陪函数」を級数で明示する．最後に第1種および第2種ルジャンドル陪函数についても紹介．
名前を混同しそうでややこしいですが、前回の「ルジャンドルの微分方程式」については
を参照ください。
\begin{equation}(1-x^2)y^{\prime\prime}-2xy'+\left[ n(n+1)-\frac{m^2}{1-x^2} \right]y=0\tag{1}\end{equation}を満たす特殊解を求める．それは「ルジャンドル陪関数 $P_n^m(x)$」とよばれる．
「ルジャンドルの陪微分方程式」は英語ではassociated Legendre differential equationと言います．「陪」がassociatedに対応しているようです．「ルジャンドルの微分方程式」というものがあって，それと関連する（associated）方程式だよということでしょうか．
方程式(1)には２つの定数 $m,n$ が含まれています．これらが実数一般である場合も考えられるのですが，今回は物理でもときどきあらわれる $m,n\in\mathbb{Z}$ の場合に限定します．また $m$ が負であっても2乗されるため，$m\ge 0$ を考えれば十分です．$n=-1$ は$0$ のときと同じ，$n=-2$ は $1$ のときと同じ方程式（以下同）となりますので $n\ge 0$ を考えればいいです．したがって $m,n\in\mathbb{Z^+}$ としましょう．
この方程式は球座標のラプラス方程式や，球座標系のヘルムホルツ方程式などであらわれます．詳細は
を参照ください．
天下り的ですが陪微分方程式(1)において $y=(1-x^2)^{m/2}u(x)$ とおくと$$y'=(1-x^2)^\frac{m}{2}u'-mx(1-x^2)^{\frac{m}{2}-1}u$$$$y^{\prime\prime}=(1-x^2)^\frac{m}{2}u^{\prime\prime}-2mx(1-x^2)^{\frac{m}{2}-1}u'+m (1-x^2)^{\frac{m}{2}-2}[(m-1)x^2-1]u$$となるので結局\begin{equation}(1-x^2)u^{\prime\prime}-2(m+1)xu'+[n(n+1)-m(m+1)]u=0\tag{2}\end{equation}となります．
ところで前回はルジャンドルの微分方程式$$(1-x^2)y^{\prime\prime}-2xy'+n(n+1)y=0\quad(n\in \mathbb{Z})$$の特殊解がルジャンドル多項式 $P_n(x)$ であるという話をしました．すると当然$$(1-x^2){P_n}^{\prime\prime}-2x{P_n}'+n(n+1)P_n=0$$が成立しています．これを $m$ 回微分すると，
$$\begin{cases}(1-x^2){P_n}^{\prime\prime\prime}-2x\cdot 2{P_n}^{\prime\prime}+[n(n+1)-2]{P_n}'=0\\(1-x^2){P_n}^{\prime\prime\prime\prime}-2x\cdot 3{P_n}^{\prime\prime\prime}+[n(n+1)-2\cdot 3]{P_n}^{\prime\prime}=0\\ \;\;\;\; \vdots \\(1-x^2)\displaystyle\frac{d^2}{dx^2}\left( \frac{d^mP_n}{dx^m}\right)-2(m+1)x\frac{d}{dx}\left( \frac{d^mP_n}{dx^m}\right)+[n(n+1)-m(m+1)]\frac{d^mP_n}{dx^m}=0\end{cases}$$
(2)式の $u(x)$ と比較して$$u(x)=\frac{d^m}{dx^m}P_n(x)$$と分かります．従ってルジャンドルの陪微分方程式(1)の特殊解は$$y(x)=(1-x^2)^\frac{m}{2}\frac{d^m}{dx^m}P_n(x) \equiv P_n^m(x)$$この $P_n^m(x)$ をルジャンドル陪関数といいます。
$$P_n^m(x)=(1-x^2)^\frac{m}{2}\frac{d^m}{dx^m}P_n(x) $$
ただし $P_n(x)$ はルジャンドル多項式．
$P_n$ は $n$ 次の多項式なので $m>n$ では $P_n^m(x)=0$ です．$m\le n$ での具体例は\begin{eqnarray*}P_1^1(x)&=&\sqrt{1-x^2}\\P_2^1(x)&=&3x\sqrt{1-x^2}\\P_2^2(x)&=&3(1-x^2)\\ P_3^1(x)&=&\frac{3}{2}(5x^2-1)\sqrt{1-x^2}\end{eqnarray*}
ちなみにルジャンドル多項式は$$P_n(x)=\sum^n_{r=0}\frac{(-n)_r(n+1)_r}{r!r!}\left(\frac{1-x}{2}\right)^r$$と表示され，これを $m$ 回微分すると $m$ 次未満の項は消えるので\begin{eqnarray*}\frac{d^mP_n}{dx^m}&=& \sum^n_{r=m} \frac{(n+r)!}{r!r!2^r(n-r)!}\frac{r!}{(r-m)!}(x-1)^{r-m}\\ &=& \frac{1}{2^m}\sum^{n-m}_{r=0}\frac{(n+m+r)!}{(r+m)!(n-m-r)!r!}\left(\frac{x-1}{2}\right)^r\end{eqnarray*} $$\therefore\quad P_n^m(x)=\frac{(1-x^2)^\frac{m}{2}}{2^m}\sum^{n-m}_{r=0}\frac{(n+m+r)!}{(r+m)!(n-m-r)!r!}\left(\frac{x-1}{2}\right)^r $$というように陪函数を明示的に表せます．
特に $n=m$ だったら楽ですね．$$P_n^n(x)=\frac{(1-x^2)^\frac{n}{2}}{2^n}\frac{(2n)!}{n!}$$
$m,n$ が非整数の場合を含んだ方程式\begin{equation}(1-x^2)y^{\prime\prime}-2xy'+\left[ \nu(\nu+1)-\frac{\mu^2}{1-x^2} \right]y=0\end{equation} の特殊解 $P_\nu^\mu(x)$ を第1種ルジャンドル陪函数といい，先ほどの $P_n^m$ に相当します．もう１つの特殊解 $Q_\nu^\mu(x)$ を第2種ルジャンドル陪函数といいます．$$P_\nu^\mu(x)=\frac{1}{\Gamma(1-\mu)}\left(\frac{1+x}{1-x}\right)^\frac{\mu}{2}{}_2F_1\left(\begin{matrix}-\nu , \nu+1 \\ 1-\mu\end{matrix} ;\frac{1-x}{2}\right)$$$$Q_\nu^\mu(x)=\frac{\sqrt{\pi}\Gamma(\mu+\nu+1)}{2^{\nu+1}\Gamma(\nu+\frac{3}{2})}e^{i\pi \mu}\frac{(x^2-1)^{\frac{\mu}{2}}}{x^{\mu+\nu+1}}{}_2F_1\left(\begin{matrix}\frac{\mu+\nu+1}{2},\frac{\mu+\nu+2}{2} \\ \nu+\frac{3}{2}\end{matrix} ;\frac{1}{x^2}\right)$$
次の記事：
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
常微分方程式シリーズ
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
