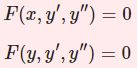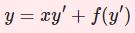クレローの方程式を難しくしたChrystalの微分方程式について解説。特別な場合には一般解と特異解が現れ、特異解が一般解の包絡線となる。この方程式は一般にはややこしいので特殊で解きやすいもののみを扱おう。
常微分方程式シリーズ過去記事
【D1】１階線型微分方程式の解法
【D2】ベルヌーイの微分方程式
【D3】クレローの方程式と包絡線（解法と例題）
$$y'^2+Axy'+By+Cx^2=0\quad (A,B,C:\mathrm{const})$$
クレローの微分方程式について調べていたら英語のウィキペディアでこのような方程式を見つけました。名前の由来は数学者George Chrystalからとのことです。スペルからして「クリスタル」かなと思うのですが、読み方不明です。検索してもこの方程式に関するサイトは全然出てきませんので、そもそも認知されているのか分かりませんが、微分方程式の記事が書ければなんだっていいので取り組んでみました。
式を見ても分かるように、かなり難解そうです。今回は無理せず、きれいな解があらわれるように私が決めた係数でやってみたのでその結果を書きました。実際、クレローの方程式を彷彿とさせる大変おもしろい解が得られました。
Wikipediaの記事によればこの方程式はまず $$4By(x)=(A^2-4C-z(x)^2)x^2$$とおいて $z(x)$ の微分方程式に書き換えることからはじめるといいそうです。これを踏まえてやってみましょう。一般の係数ではしんどそうなので次の微分方程式を本記事の例題とします。
$$y'^2+2xy'-y+\frac{x^2}{2}=0$$
次のようにおいて $y(x)$ を $z(x)$ へ置き換えます。\begin{equation}y=-\frac{x^2}{4}(2-z^2)\tag{1}\end{equation}1階微分は$$y'=-\frac{x}{2}(2-z^2)+\frac{x^2}{2}zz'$$となります。$y,y'$ を方程式に代入すると\begin{eqnarray*}&&y'^2+2xy'-y+\frac{x^2}{2}=0\\&\Leftrightarrow& \left[\frac{x^2}{2}zz'-\frac{x}{2}(2-z^2)\right]^2+2x\left[\frac{x^2}{2}zz'-\frac{x}{2}(2-z^2)\right]+\frac{x^2}{4}(2-z^2)+\frac{x^2}{2}=0\\ &\Leftrightarrow& \frac{x^2}{4}\left[xzz'-(2-z^2)\right]^2+x^2\left[xzz'-(2-z^2)\right]+\frac{x^2}{4}(2-z^2)+\frac{x^2}{2}=0 \\ &\Leftrightarrow& \left[xzz'-(2-z^2)\right]^2+4\left[xzz'-(2-z^2)\right]+4-z^2=0\\ &\Leftrightarrow& (xzz'+z^2-z)(xzz'+z^2+z)=0 \\ &\Leftrightarrow& z^2(xz'+z-1)(xz'+z+1)=0 \end{eqnarray*}よって $z(x)$ は以下の３つの方程式のいずれかを満たせばいいことになります。$$\begin{cases}z=0 \\ xz'+z+1=0 \\xz'+z-1=0\end{cases}$$順に見ていきましょう。
(1)より $z=0$ ならば
$$y=-\frac{x^2}{2}$$
と解の１つが求まります。実際、元の方程式に代入するとこれを満たしています。この解には任意定数がついておらず、あとで特異解であることが判明します。
残りの2つはまとめて$$xz'+z\pm 1=0$$と書くことにします。変数分離ができて$$\frac{dz}{z\pm 1}=-\frac{dx}{x}$$積分すると$$\log|z\pm 1|=-\log|x|+c'$$積分定数を置きなおせば$$\log|z\pm 1|=\log\left|\frac{C'}{x}\right|$$とできます。対数を外したあと、$C'$ は任意であるため正も負もとりうることから絶対値を取り払って問題ありません。よって$$z=\frac{C'}{x}\mp 1$$(1)へ代入して\begin{eqnarray*}y&=&-\frac{x^2}{4}(2-z^2)\\ &=&\frac{x^2}{4}\left[\left(\frac{C'}{x}\mp 1\right)^2-2\right] \\ &=& \frac{x^2}{4}\left[\frac{C'^2}{x^2}\mp \frac{2C'}{x}-1\right] \\ &=& \frac{C'^2}{4}\mp \frac{C'}{2}x-\frac{x^2}{4}\end{eqnarray*}$C'=2c$ とあらためて$$y=c^2\mp cx-\frac{x^2}{4}$$$c$ は正も負もとりうるので複号を外します。以上により
$$y=c^2+cx-\frac{x^2}{4}$$
なる解を得ました。任意定数があるのでこれが一般解となります。この一般解は先ほどの解を含んでいません。よって解をまとめると
一般解は曲線群 $$y=c^2+cx-\frac{x^2}{4}$$特異解は $$y=-\frac{x^2}{2}$$
です。これですべての解を得られました！
おもしろいのは特異解と一般解の間にはちゃんと関係があるということです。
一般解は $c$ を任意に変化させることで2次関数をたくさん作りだします。一般解を$$F(x,y,c)\equiv c^2+cx-\frac{x^2}{4} -y=0$$と書くことにします。ここでたくさんの2次関数たちが生み出す包絡線を求めてみます。包絡線は連立方程式$$F(x,y,c)=0\;,\;\frac{\partial F}{\partial c}=0$$の $c$ を消去することで導出できます。すなわち$$\begin{cases}c^2+cx-\displaystyle\frac{x^2}{4} -y=0 \\ 2c+x=0\end{cases}$$$$\therefore \quad y=-\frac{x^2}{2}$$これが包絡線となります。特異解と一致していますね。従ってぜんぶ話をまとめると
微分方程式$$y'^2+2xy'-y+\frac{x^2}{2}=0$$の一般解は曲線群 $$y=c^2+cx-\frac{x^2}{4}$$であり、その包絡線は特異解 $$y=-\frac{x^2}{2}$$に一致する。
特異解が一般解の包絡線になっているというのは、クレローの方程式のときもありましたよね（記事冒頭のリンク）。なのでChrystalの微分方程式はクレローのムズい版みたいだなと思いました。
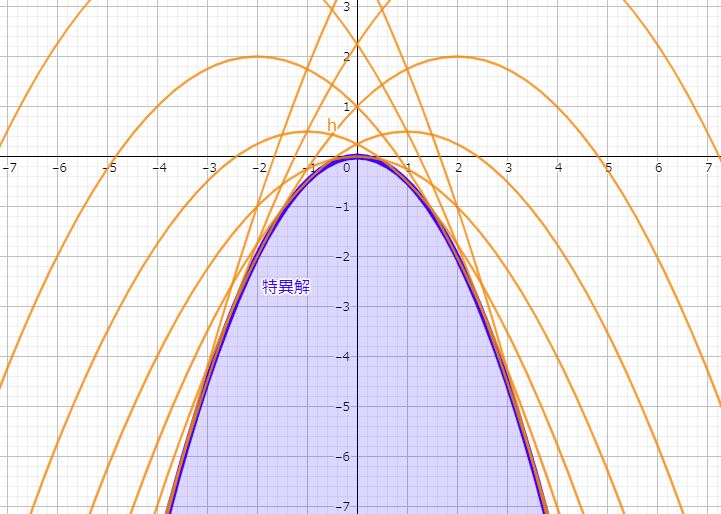
さすがに2次関数だらけで分かりにくいですね。クレローのときは直線群だったのでまだ分かりやすかったですが。
常微分シリーズ
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
