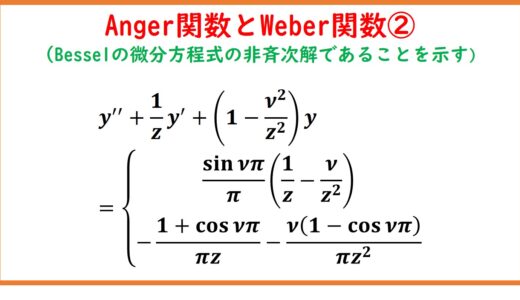
\begin{eqnarray}\mathbf{J}_\nu(z) &=& \frac{1}{\pi}\int_0^\pi\cos(\nu\t-z\sin\t)d\t\tag{1}\\ \mathbf{E}_\nu(z) &=& \frac{1}{\pi}\int_0^\pi\sin(\nu\t-z\sin\t)d\t\tag{2}\end{eqnarray}と定義するとき、一般化された超幾何関数を用いることで次のように表現できる。\begin{eqnarray*}\mathbf{J}_\nu(z) &=& \frac{\sin\nu\pi}{\nu\pi}{}_1F_2\left[\begin{matrix}1\\1-\frac{\nu}{2},1+\frac{\nu}{2}\end{matrix};-\frac{z^2}{4}\right]\\&&+\frac{\sin\nu\pi}{(1-\nu^2)\pi}z\;{}_1F_2\left[\begin{matrix}1\\\frac{3-\nu}{2},\frac{3+\nu}{2}\end{matrix};-\frac{z^2}{4}\right]\end{eqnarray*}\begin{eqnarray*}\mathbf{E}_\nu(z) &=& \frac{1-\cos\nu\pi}{\nu\pi}{}_1F_2\left[\begin{matrix}1\\1-\frac{\nu}{2},1+\frac{\nu}{2}\end{matrix};-\frac{z^2}{4}\right]\\&&-\frac{1+\cos\nu\pi}{(1-\nu^2)\pi}z\;{}_1F_2\left[\begin{matrix}1\\\frac{3-\nu}{2},\frac{3+\nu}{2}\end{matrix};-\frac{z^2}{4}\right]\end{eqnarray*}
明確に決まった名前があるかは分かりませんが、英語版Wikipediaによると(1)をAnger関数、(2)をWeber関数といいます(後者は同名の異なる関数があった気がする)。ともにWatson(1966)のChapter10で紹介されています。
第1種ベッセル関数 $J_\nu(x)$ はSchläefliの積分表示により\begin{equation}J_\nu(z)=\frac{1}{\pi}\int^\pi_0\cos(\nu\theta-z\sin\t)d\theta-\frac{\sin\nu\pi}{\pi}\int_0^\infty e^{-\nu t-z\sinh t}dt\tag{3}\end{equation}と表されます*。$\nu$ が整数 $n$ なら右辺の第2項はゼロとなりますので\begin{equation}J_n(z)=\frac{1}{\pi}\int^\pi_0\cos(n\theta-z\sin\t)d\theta\tag{4}\end{equation}となり、(1)の $\mathbf{J}_\nu(z)$ に一致します。ベッセル関数の定義や $J_n(z)$ の積分表示については
をご覧ください。
* Watson, A Treatise On The Theory Of Bessel Functions second edition(1966)のp176より
(1)(2)を級数展開しましょう。加法定理でバラして\begin{eqnarray*}\mathbf{J}_\nu(z) &=& \frac{1}{\pi}\int_0^\pi\cos\nu\t\cos(z\sin\t)d\t+\frac{1}{\pi}\int_0^\pi\sin\nu\t\sin(z\sin\t)d\t\\\ \mathbf{E}_\nu(z) &=& \frac{1}{\pi}\int_0^\pi\sin\nu\t\cos(z\sin\t)d\t-\frac{1}{\pi}\int_0^\pi\cos\nu\t\sin(z\sin\t)d\t\end{eqnarray*} $\sin x$ と $\cos x$ のマクローリン展開より\begin{eqnarray}\mathbf{J}_\nu(z) &=& \frac{1}{\pi}\sum_{m=0}^\infty\frac{(-1)^m z^{2m}}{(2m)!}\int_0^\pi\cos\nu\t \sin^{2m}\t d\t\\&&+\frac{1}{\pi}\sum_{m=0}^\infty\frac{(-1)^m z^{2m+1}}{(2m+1)!}\int_0^\pi\sin\nu\t \sin^{2m+1}\t d\t\tag{5}\\ \mathbf{E}_\nu(z) &=& \frac{1}{\pi}\sum_{m=0}^\infty\frac{(-1)^m z^{2m}}{(2m)!}\int_0^\pi\sin\nu\t \sin^{2m}\t d\t\\&&-\frac{1}{\pi}\sum_{m=0}^\infty\frac{(-1)^m z^{2m+1}}{(2m+1)!}\int_0^\pi\cos\nu\t \sin^{2m+1}\t d\t\tag{6}\end{eqnarray}この積分が問題となります。$\nu$ は実数で $m$ は非負整数です。収束・発散の議論を簡単のため、とりあえず $\nu\notin\ZZ$ としておきます。
上記、加法定理でばらしたところで、$\nu$ が偶数のときは $\mathbf{J}_\nu(z)$ の第2項と $\mathbf{E}_\nu(z)$ の第1項が $0$ となります。また $\nu$ が奇数のときは $\mathbf{J}_\nu(z)$ の第1項と $\mathbf{E}_\nu(z)$ の第2項が $0$ となります。積分区間を半分で分けてみると分かります。
において、複素積分の手法を用いることにより次の公式を得ました。$s>0$ のとき\begin{equation}\int_0^\pi\sin^{s-1}\t\sin a\t d\t=\frac{\pi\sin\frac{\pi a}{2}}{2^{s-1}sB(\frac{s+a+1}{2},\frac{s-a+1}{2})}\tag{7}\end{equation}同様にして次の式も成り立ちます。\begin{equation}\int_0^\pi\sin^{s-1}\t\cos a\t d\t=\frac{\pi\cos\frac{\pi a}{2}}{2^{s-1}sB(\frac{s+a+1}{2},\frac{s-a+1}{2})}\tag{8}\end{equation}(5)の積分へ適用すると\begin{eqnarray*}\int_0^\pi\cos\nu\t \sin^{2m}\t d\t &=& \frac{\pi\cos\frac{\nu\pi}{2}}{2^{2m}(2m+1)B(\frac{2m+2+\nu}{2},\frac{2m+2-\nu}{2})}\\ &=& \frac{\pi(2m)!\cos\frac{\nu\pi}{2}}{2^{2m}\G(m+1+\frac{\nu}{2})\G(m+1-\frac{\nu}{2})}\end{eqnarray*}ガンマ関数をポッホハマー記号で書き換えます。\begin{eqnarray*}\int_0^\pi\cos\nu\t \sin^{2m}\t d\t &=&\frac{\pi(2m)!\cos\frac{\nu\pi}{2}}{2^{2m}\G(1+\frac{\nu}{2})\G(1-\frac{\nu}{2})(1+\frac{\nu}{2})_m(1-\frac{\nu}{2})_m}\\ &=& \frac{\pi(2m)!\cos\frac{\nu\pi}{2}}{2^{2m}\frac{\nu}{2}\G(\frac{\nu}{2})\G(1-\frac{\nu}{2})(1+\frac{\nu}{2})_m(1-\frac{\nu}{2})_m}\\ &=& \frac{(2m)!\cdot2\cos\frac{\nu\pi}{2}\sin\frac{\nu\pi}{2}}{2^{2m}\nu(1+\frac{\nu}{2})_m(1-\frac{\nu}{2})_m}\end{eqnarray*}最後はガンマ関数の相反公式を使いました。ここで三角比の倍角の公式から\begin{equation}\int_0^\pi\cos\nu\t \sin^{2m}\t d\t = \frac{(2m)!\sin\nu\pi}{2^{2m}\nu(1+\frac{\nu}{2})_m(1-\frac{\nu}{2})_m}\tag{9}\end{equation}を得ます。次に(5)の第2項の積分は\begin{eqnarray*}\int_0^\pi\sin\nu\t \sin^{2m+1}\t d\t &=& \frac{\pi\sin\frac{\nu\pi}{2}}{2^{2m+1}(2m+2)B(\frac{2m+3+\nu}{2},\frac{2m+3-\nu}{2})} \\ &=& \frac{\pi(2m+1)!\sin\frac{\nu\pi}{2}}{2^{2m+1}\G(m+\frac{3+\nu}{2})\G(m+\frac{3-\nu}{2})} \\ &=& \frac{\pi(2m+1)!\sin\frac{\nu\pi}{2}}{2^{2m+1}\G(\frac{3+\nu}{2})\G(\frac{3-\nu}{2})(\frac{3+\nu}{2})_m(\frac{3-\nu}{2})_m}\\ &=& \frac{\pi(2m+1)!\sin\frac{\nu\pi}{2}}{2^{2m+1}\frac{1+\nu}{2}\frac{1-\nu}{2}\G(\frac{1+\nu}{2})\G(\frac{1-\nu}{2})(\frac{3+\nu}{2})_m(\frac{3-\nu}{2})_m} \\ &=& \frac{(2m+1)!\cdot 2\sin\frac{\nu\pi}{2}\sin\frac{\pi(1-\nu)}{2}}{2^{2m}(1-\nu^2)(\frac{3+\nu}{2})_m(\frac{3-\nu}{2})_m} \\ &=&\frac{(2m+1)!\cdot \sin\nu\pi}{2^{2m}(1-\nu^2)(\frac{3+\nu}{2})_m(\frac{3-\nu}{2})_m}\end{eqnarray*}よって\begin{equation}\int_0^\pi\sin\nu\t \sin^{2m+1}\t d\t = \frac{(2m+1)!\cdot \sin\nu\pi}{2^{2m}(1-\nu^2)(\frac{3+\nu}{2})_m(\frac{3-\nu}{2})_m}\tag{10}\end{equation}(9)(10)を(5)に適用して\begin{eqnarray*}\mathbf{J}_\nu(z) &=& \frac{1}{\pi}\sum_{m=0}^\infty\frac{(-1)^m z^{2m}}{(2m)!} \frac{(2m)!\sin\nu\pi}{2^{2m}\nu(1+\frac{\nu}{2})_m(1-\frac{\nu}{2})_m}\\&&+\frac{1}{\pi}\sum_{m=0}^\infty\frac{(-1)^m z^{2m+1}}{(2m+1)!} \frac{(2m+1)!\cdot \sin\nu\pi}{2^{2m}(1-\nu^2)(\frac{3+\nu}{2})_m(\frac{3-\nu}{2})_m}\end{eqnarray*}整理しましょう.\begin{eqnarray}\mathbf{J}_\nu(z) &=& \frac{\sin\nu\pi}{\nu\pi}\sum_{m=0}^\infty\frac{1}{(1+\frac{\nu}{2})_m(1-\frac{\nu}{2})_m}\left(-\frac{z^2}{4}\right)^m\\&&+\frac{\sin\nu\pi}{(1-\nu^2)\pi}z\sum_{m=0}^\infty\frac{1}{(\frac{3+\nu}{2})_m(\frac{3-\nu}{2})_m}\left(-\frac{z^2}{4}\right)^m\tag{11}\end{eqnarray}第1項は $z$ の偶数次の級数、第2項は奇数次の級数であることが分かります。
(6)の積分についてもここまでと同様にして\begin{equation}\int_0^\pi\sin\nu\t \sin^{2m}\t d\t=\frac{(2m)!(1-\cos\nu\pi)}{2^{2m}\nu(1+\frac{\nu}{2})_m(1-\frac{\nu}{2})_m}\tag{12}\end{equation}\begin{equation}\int_0^\pi\cos\nu\t \sin^{2m+1}\t d\t = \frac{(2m+1)!\cdot (1+\cos\nu\pi)}{2^{2m}(1-\nu^2)(\frac{3+\nu}{2})_m(\frac{3-\nu}{2})_m}\tag{13}\end{equation}を適用すると\begin{eqnarray}\mathbf{E}_\nu(z) &=& \frac{1-\cos\nu\pi}{\nu\pi}\sum_{m=0}^\infty\frac{1}{(1+\frac{\nu}{2})_m(1-\frac{\nu}{2})_m}\left(-\frac{z^2}{4}\right)^m\\&&-\frac{1+\cos\nu\pi}{(1-\nu^2)\pi}z\sum_{m=0}^\infty\frac{1}{(\frac{3+\nu}{2})_m(\frac{3-\nu}{2})_m}\left(-\frac{z^2}{4}\right)^m\tag{14}\end{eqnarray}
これで終わりでも構いませんが、一般化された超幾何級数 ${}_pF_{q}$ を用いると、$n!=(1)_n$ であることに留意して
\begin{eqnarray}\mathbf{J}_\nu(z) &=& \frac{\sin\nu\pi}{\nu\pi}{}_1F_2\left[\begin{matrix}1\\1-\frac{\nu}{2},1+\frac{\nu}{2}\end{matrix};-\frac{z^2}{4}\right]\\&&+\frac{\sin\nu\pi}{(1-\nu^2)\pi}z\;{}_1F_2\left[\begin{matrix}1\\\frac{3-\nu}{2},\frac{3+\nu}{2}\end{matrix};-\frac{z^2}{4}\right]\tag{15}\end{eqnarray}\begin{eqnarray}\mathbf{E}_\nu(z) &=& \frac{1-\cos\nu\pi}{\nu\pi}{}_1F_2\left[\begin{matrix}1\\1-\frac{\nu}{2},1+\frac{\nu}{2}\end{matrix};-\frac{z^2}{4}\right]\\&&-\frac{1+\cos\nu\pi}{(1-\nu^2)\pi}z\;{}_1F_2\left[\begin{matrix}1\\\frac{3-\nu}{2},\frac{3+\nu}{2}\end{matrix};-\frac{z^2}{4}\right]\tag{16}\end{eqnarray}
と、冒頭の式を得ることができました!例えば\begin{eqnarray}\mathbf{E}_\frac{1}{2}(1) &=& \frac{2}{\pi}{}_1F_2\left[\begin{matrix}1\\\frac{3}{4},\frac{5}{4}\end{matrix};-\frac{1}{4}\right]\\&&-\frac{4}{3\pi}\;{}_1F_2\left[\begin{matrix}1\\\frac{5}{4},\frac{7}{4}\end{matrix};-\frac{1}{4}\right]\end{eqnarray}ですので\begin{eqnarray}\int_0^\pi\sin\left(\frac{\t}{2}-\sin\t\right)d\t &=& 2{}_1F_2\left[\begin{matrix}1\\\frac{3}{4},\frac{5}{4}\end{matrix};-\frac{1}{4}\right]-\frac{4}{3}\;{}_1F_2\left[\begin{matrix}1\\\frac{5}{4},\frac{7}{4}\end{matrix};-\frac{1}{4}\right]\\&\approx&0.313\end{eqnarray}のようになります。
(15)(16)の式は $\nu\notin\ZZ$ では特に問題ありませんが $\nu\in\ZZ$ では発散するおそれがあるように見えます。(1)(2)の答えとしてふさわしいか、ざっと確認してみましょう。
ν=0のとき
$\nu=0$ あるいは $\nu\to0$ の極限を考えると\begin{eqnarray}\mathbf{J}_0(z) &=& {}_1F_2\left[\begin{matrix}1\\1,1\end{matrix};-\frac{z^2}{4}\right]\\&=&\sum_{m=0}^\infty\frac{1}{m!m!}\left(-\frac{z^2}{4}\right)^m\end{eqnarray}\begin{eqnarray}\mathbf{E}_0(z) &=&-\frac{2}{\pi}z\;{}_1F_2\left[\begin{matrix}1\\\frac{3}{2},\frac{3}{2}\end{matrix};-\frac{z^2}{4}\right]\end{eqnarray}のように表せます。これらについては(1)(2)の右辺を計算しても同じ結果を得るのでOKです。
例えば$$\mathbf{J}_0(z)=\frac{1}{\pi}\int_0^\pi\cos(z\sin\t)d\t$$で $\cos$ を展開すればよい。第1種ベッセル関数 $J_0(z)$ と同じ級数表現となる。
νが偶数のとき
$\nu$ が自然数の偶数のときを考えます。式の形からして負整数については省略してもよいでしょう。$\nu=2n$ とすると\begin{eqnarray}\mathbf{J}_{2n}(z) &=& \frac{1}{2n\pi}\displaystyle\lim_{\nu\to2n}\sum_{m=0}^\infty\frac{\sin\nu\pi}{(1-\frac{\nu}{2})_m(1+n)_m}\left(-\frac{z^2}{4}\right)^m\end{eqnarray}分子に $\sin$ があり、その極限は $0$ です。なので $m<n$ の項は単純に $0$ となります。$m\ge n$ の項では、分母に極限がゼロとなる因数が1つ現れます。 $$(1-\frac{\nu}{2})_m=(1-\frac{\nu}{2})(2-\frac{\nu}{2})\cdots\underbrace{(n-\frac{\nu}{2})}_{\mathrm{goes\;to}\; 0}\cdots(m-\frac{\nu}{2})$$ここに着目して極限をとると$$\displaystyle\lim_{\nu\to2n}\frac{\sin\nu\pi}{n-\frac{\nu}{2}}=-2\pi$$したがって\begin{eqnarray*}\mathbf{J}_{2n}(z)&=&\frac{-1}{n}\sum_{m=n}^\infty\frac{\left(-\frac{z^2}{4}\right)^m}{(1-n)(2-n)\cdots(n-1-n)\times(n+1-n)\cdots(m-n)(1+n)_m} \\&=&\frac{(-1)^n}{n!}\sum_{m=n}^\infty\frac{\left(-\frac{z^2}{4}\right)^m}{(n+1-n)\cdots(m-n)(1+n)_m} \end{eqnarray*}$m$ をずらして、とる和のスタートを $0$ からにすると\begin{eqnarray*}\mathbf{J}_{2n}(z)&=&\frac{(-1)^n}{n!}\sum_{m=0}^\infty\frac{\left(-\frac{z^2}{4}\right)^{m+n}}{m!(1+n)_{m+n}}\\&=& \sum_{m=0}^\infty\frac{(-1)^m}{m!(m+2n)!}\left(\frac{z}{2}\right)^{2m+2n}\end{eqnarray*}これは第1種ベッセル関数と全く同じ級数です。よって第1種ベッセル関数に等しいことが分かります。よって(15)は $\nu\to2n$ の極限をとることで成立しているといえます。
一方(16)に関しては、$\nu=2n$ とすると第1項の超幾何級数において分母に $0$ となる因子が1つ現れます。しかし $1-\cos\nu\pi$ では $\nu=2n$ が2位の零点となることから、この項はゼロとなります(まともに極限計算しても分かります)。したがって$$\mathbf{E}_{2n}(z) =-\frac{2}{(1-4n^2)\pi}z\;{}_1F_2\left[\begin{matrix}1\\\frac{3-2n}{2},\frac{3+2n}{2}\end{matrix};-\frac{z^2}{4}\right]$$とあらわされます。
νが奇数のとき
$\nu=2n-1$ のときは、(15)の第1項はゼロ、第2項で先ほどと同様な極限計算をします。一方、(16)の第2項はゼロとなります。
以上より(15)(16)は実数 $\nu$ において成立します。なお $\nu$ が偶数のときは $\mathbf{J}_\nu(z)$ の第2項と $\mathbf{E}_\nu(z)$ の第1項が $0$ となります。また $\nu$ が奇数のときは $\mathbf{J}_\nu(z)$ の第1項と $\mathbf{E}_\nu(z)$ の第2項が $0$ となります。
なお、ここによれば Anger関数とWeber関数はともに整関数であり、全 $z$ 平面で値をとります。
次回はAnger関数とWeber関数が満たす微分方程式や漸化式等を考えていきます。
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。