Thanks to @AlbahariRicardo :
$$I=\int_0^\infty\frac{\cos x-e^{-x}}{x}dx$$
Considering $e^{iz}$, we can see that $e^{ix}$ appears on the real axis and $e^{-y}$ appears on the imaginary axis.
Define $f(z)=\dfrac{e^{iz}}{z}$,$$\oint_Cf(z)dz=0$$
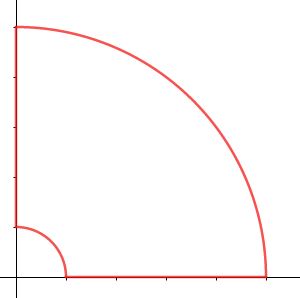
The contour C consists of two arcs of radius $\epsilon$ , $R$ and two lines.
\begin{eqnarray*}0&&=\int_\epsilon^R\frac{e^{ix}}{x}dx+\int_0^\frac{\pi}{2}\frac{e^{iRe^{i\t}}}{Re^{i\t}}iRe^{i\t}d\t\\&&\quad+\int_R^\epsilon\frac{e^{-y}}{iy}idy+\int_\frac{\pi}{2}^0\frac{e^{i\epsilon e^{i\t}}}{\epsilon e^{i\t}}i\epsilon e^{i\t}d\t\\&&=\int_0^\infty\frac{e^{ix}-e^{-x}}{x}dx+i\int_0^\frac{\pi}{2}e^{iRe^{i\t}}d\t\\&&\quad-i\int_0^\frac{\pi}{2}e^{i\epsilon e^{i\t}}d\t\\&&=\int_0^\infty\frac{e^{ix}-e^{-x}}{x}dx+i\int_0^\frac{\pi}{2}e^{iRe^{i\t}}d\t-\frac{\pi}{2}i\end{eqnarray*}
The integral of the big arc tends to 0 as $R\to\infty$ since\begin{eqnarray*}\left|\int_0^\frac{\pi}{2}e^{iRe^{i\t}}d\t\right|&&\le\int_0^\frac{\pi}{2}e^{-R\sin\t}d\t\\&&\le\int_0^\frac{\pi}{2}e^{-\frac{2R}{\pi}\t}d\t\\&&=\frac{\pi}{2R}(1-e^{-R})\longrightarrow 0\end{eqnarray*}Therefore,$$0=\int_0^\infty\frac{e^{ix}-e^{-x}}{x}dx-\frac{\pi}{2}i$$Now we get$$\int_0^\infty\frac{\cos x-e^{-x}}{x}dx=0\;,\;\int_0^\infty\frac{\sin x}{x}dx=\frac{\pi}{2}$$
Another solution
$$\int_0^\infty\frac{\cos x-e^{-x}}{x}dx=-\mathrm{Ci}(\epsilon)-\mathrm{Ei}(\epsilon)\\=-\gamma-\log\epsilon+\gamma+\log\epsilon=0$$
Other examples:
Integrals and Miscellaneous 1
複素積分演習（cos(log x)/(1+x^2)）
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
