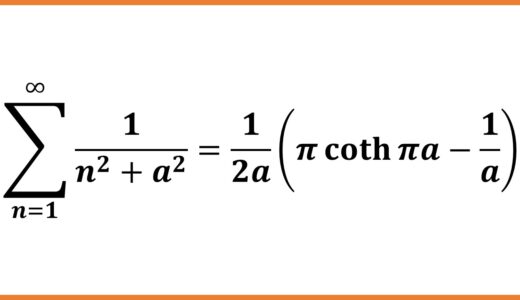Integrals and Miscellaneous 3

$$I=\int_0^\infty\left(\sqrt{1+x^4}-x^2\right)^sdx$$ Let $$y=\left(\sqrt{1+x^4}-x^2\right)^2$$ Then,

$$\begin{eqnarray*}I&&=\frac{1}{4\sqrt{2}}\int_0^1\left[y^{\frac{s}{2}-\frac{5}{4}}(1-y)^{\frac{1}{2}}+2y^{\frac{s}{2}-\frac{1}{4}}(1-y)^{-\frac{1}{2}}\right]dy\\&&=\frac{1}{4\sqrt{2}}\left[B\left(\frac{s}{2}-\frac{1}{4},\frac{3}{2}\right)+2B\left(\frac{s}{2}+\frac{3}{4},\frac{1}{2}\right)\right]\\&&=\frac{1}{4\sqrt{2}}\left[\frac{\G(\frac{s}{2}-\frac{1}{4})\frac{\sqrt{\pi}}{2}}{\G(\frac{s}{2}+\frac{5}{4})}+2\frac{\G(\frac{s}{2}+\frac{3}{4})\sqrt{\pi}}{\G(\frac{s}{2}+\frac{5}{4})}\right]\\&&=\sqrt{\frac{\pi}{2}}\frac{(\frac{1}{2}+s-\frac{1}{2})\G(\frac{s}{2}-\frac{1}{4})}{(2s+1)\G(\frac{s}{2}+\frac{1}{4})}\\&&=\frac{s}{2s+1}\sqrt{\frac{\pi}{2}}\frac{\G(\frac{s}{2}-\frac{1}{4})}{\G(\frac{s}{2}+\frac{1}{4})}\end{eqnarray*}$$

$$I=\int_0^\infty\frac{\sin sx}{e^{2\pi x}-1}dx$$ Abel-Plana formula: $$\begin{multline}\sum_{k=m}^nf(k)=\frac{f(m)+f(n)}{2}+\int_m^nf(z)dz\\+i\int_0^\infty\frac{f(m+iy)-f(m-iy)-f(n+iy)+f(n-iy)}{e^{2\pi y}-1}dy\end{multline}$$

Let $f(z)=e^{-sz}$ , $m=0$ , $n=\infty$ , we have $$\sum_{k=0}^\infty e^{-sk}=\frac{1}{2}+\int_0^\infty e^{-sx}dx+i\int_0^\infty\frac{e^{-isy}-e^{isy}}{e^{2\pi y}-1}dy$$ Therefore, $$\frac{1}{1-e^{-s}}=\frac{1}{2}+\frac{1}{s}+2\int_0^\infty\frac{\sin sx}{e^{2\pi x}-1}dx$$ Hence, $$I=\frac{1}{2}\left(\frac{1}{1-e^{-s}}-\frac{1}{s}-\frac{1}{2}\right)$$

Another solution:

$$\begin{eqnarray*}I&&=\int_0^\infty\sin sx\sum_{n=1}^\infty e^{-2\pi nx}dx\\&&=\sum_{n=1}^\infty\int_0^\infty e^{-2\pi nx}\sin sx dx\end{eqnarray*}$$

This integral can be evaluated like this: $$\begin{eqnarray*}\int_0^\infty e^{-2\pi nx}\sin sx dx&&=\left[-\frac{e^{-2\pi nx}}{2\pi n}\sin sx\right]_0^\infty+\frac{s}{2\pi n}\int_0^\infty e^{-2\pi nx}\cos sx dx\\&&=\left[-\frac{se^{-2\pi nx}}{4\pi^2 n^2}\cos sx\right]_0^\infty-\frac{s^2}{4\pi^2 n^2}\int_0^\infty e^{-2\pi nx}\sin sx dx\end{eqnarray*}$$ Hence, $$\int_0^\infty e^{-2\pi nx}\sin sx dx=\frac{s}{s^2+4\pi^2n^2}$$

$$\begin{eqnarray*}I&&=\sum_{n=1}^\infty\frac{s}{s^2+4\pi^2n^2}\\&&=\frac{1}{4}\left(\coth\frac{s}{2}-\frac{2}{s}\right)=\frac{1}{2}\left(\frac{1}{1-e^{-s}}-\frac{1}{s}-\frac{1}{2}\right)\end{eqnarray*}$$

See below about Abel-Plana summatioin formula:

2022年3月5日 アベル・プラナの和公式　複素積分を応用して

See below about a series formula involving $\coth x$:

2022年2月4日 $\sum\frac{1}{n^2+1}$の値（複素フーリエ級数）

$$I=\int_0^\infty x^{s-1}e^{ix}dx$$ Consider $$0=\oint_Cz^{s-1}e^{iz}dz$$ Contour $C$ starts at the origin, go right along the real axis to $R$, then draw the quadrant of radius $R$ counter-clockwise, go back to the origin along the imaginary axis. $$\begin{eqnarray*}0&&=\int_0^\infty x^{s-1}e^{ix}dx+\int_0^\frac{\pi}{2}iR^se^{is\t}e^{iR\cos\t-R\sin\t}d\t-e^{\frac{\pi}{2}si}\int_0^\infty y^{s-1}e^{-y}dy\end{eqnarray*}$$ The second integral tends to 0 as $R\to\infty$ when $\mathfrak{R}s<1$.

So we suppose that $\mathfrak{R}s<1$.Then, $$I=e^{\frac{\pi}{2}si}\int_0^\infty y^{s-1}e^{-y}dy=\G(s)e^{\frac{\pi}{2}si}$$ Hence, $$\begin{cases}\displaystyle\int_0^\infty x^{s-1}\cos xdx&=&\G(s)\cos\dfrac{\pi s}{2}\\\displaystyle\int_0^\infty x^{s-1}\sin xdx&=&\G(s)\sin\dfrac{\pi s}{2}\end{cases}$$

From @integralsbot $$\int_0^\frac{\pi}{2}\frac{dx}{\sqrt[3]{1+3\sin^2 x}}=\frac{\G^3(\frac{1}{3})}{2^{\frac{7}{3}}\pi}$$ PROOF. $$\begin{eqnarray*}LHS&&=\int_0^\frac{\pi}{2}\frac{dx}{\sqrt[3]{1+3\sin^2 x}}\\&&=\int_0^\frac{\pi}{2}\sum_{n=0}^\infty \left(\frac{1}{3}\right)_n\frac{(-3\sin^2x)^n}{n!}dx\\&&=\sum_{n=0}^\infty \frac{(\frac{1}{3})_n}{n!}(-3)^n\int_0^\frac{\pi}{2}\sin^{2n}xdx\\&&=\frac{\pi}{2}\sum_{n=0}^\infty\frac{(\frac{1}{3})_n(\frac{1}{2})_n}{(1)_n}\frac{(-3)^n}{n!}\\&&=\frac{\pi}{2}F\left(\frac{1}{3},\frac{1}{2},1;-3\right)\end{eqnarray*}$$ Recall Bailey's identity $$\begin{equation}F\left(a,b,2b;-\frac{4z}{(1-z)^2}\right)=(1-z)^{2a}F\left(a,a-b+\frac{1}{2},b+\frac{1}{2};z^2\right)\tag{1}\end{equation}$$ Let $z=\frac{1}{3}$ , $a=\frac{1}{3}$ , $b=\frac{1}{2}$ to get $$F\left(\frac{1}{3},\frac{1}{2},1;-3\right)=\left(\frac{2}{3}\right)^{\frac{2}{3}}F\left(\frac{1}{3},\frac{1}{3},1;\frac{1}{9}\right)$$ Moreover, recall a formula deduced here, namely $$\begin{equation}F\left(a,\frac{1-a}{2},\frac{3a+5}{6};\frac{1}{9}\right)=\left(\frac{3}{4}\right)^\frac{a}{2}\frac{\G(\frac{3a+5}{6})\G(\frac{2}{3})}{\G(\frac{3a+4}{6})\G(\frac{5}{6})}\tag{2}\end{equation}$$ After setting $a=\frac{1}{3}$, duplication formula and reflection formula gives $$F\left(\frac{1}{3},\frac{1}{3},1;\frac{1}{9}\right)=\frac{3^\frac{2}{3}\G^3(\frac{1}{3})}{4\pi^2}$$ Therefore, $$\int_0^\frac{\pi}{2}\frac{dx}{\sqrt[3]{1+3\sin^2 x}}=\frac{\G^3(\frac{1}{3})}{2^{\frac{7}{3}}\pi}$$

$$\begin{eqnarray*}I&&=\int_0^\infty\frac{\cos 2bx}{\cosh ax}dx\\&&=2\int_0^\infty\frac{e^{-ax}\cos 2bx}{1+e^{-2ax}}dx\\&&=2\int_0^\infty e^{-ax\cos2bx}\sum_{n=0}^\infty(-e^{-2ax})^ndx\\&&=2\sum_{n=0}^\infty(-1)^n\int_0^\infty e^{-(2n+1)ax}\cos2bxdx\end{eqnarray*}$$ The rightmost side is evaluated by integration by parts twice then, $$\int_0^\infty e^{-(2n+1)ax}\cos2bxdx=\frac{(2n+1)a}{(2n+1)^2a^2+4b^2}$$ Hence, $$\begin{eqnarray*}I&&=2a\sum_{n=0}^\infty\frac{(-1)^n(2n+1)}{(2n+1)^2a^2+4b^2}\\&&=\frac{\pi^2}{2a}\sum_{n=0}^\infty\frac{(-1)^n(2n+1)}{\pi^2(n+\frac{1}{2})^2+\frac{b^2}{a^2}\pi^2}\end{eqnarray*}$$ Using the series representation of $\mathrm{sech} z$: $$\mathrm{sech} \:z=\pi\sum_{n=0}^\infty\frac{(-1)^n(2n+1)}{\pi^2(n+\frac{1}{2})^2+z^2}$$ We obtain $$I=\frac{\pi}{2a}\mathrm{sech}\:\frac{b}{a}\pi$$

$$I\equiv\int_0^\frac{\pi}{2}\frac{\arctan\sqrt{\tan x}}{\tan x}dx$$

proof here:

2022年4月10日 複素積分演習(arctan z/z(1+z^4))

$$\begin{eqnarray*}I&&=\int\frac{1+x^2}{1+x^4}dx\\&&=\frac{1}{2}\int\left(\frac{1}{x^2+\sqrt{2}x+1}+\frac{1}{x^2-\sqrt{2}x+1}\right)dx\\&&=\frac{1}{2}\int\frac{dx}{(x+\frac{1}{\sqrt{2}})^2+\frac{1}{2}}+\frac{1}{2}\int\frac{dx}{(x-\frac{1}{\sqrt{2}})^2+\frac{1}{2}}\\&&=\frac{\arctan(\sqrt{2}x+1)+\arctan(\sqrt{2}x-1)}{\sqrt{2}}+C\\&&=\frac{1}{\sqrt{2}}\arctan\frac{\sqrt{2}x}{1-x^2}+C\end{eqnarray*}$$

$$\begin{eqnarray*}I&&=\int_0^\infty\frac{\arctan x}{x^{\log x+1}}dx&&=\int_0^1\frac{\arctan x}{x^{\log x+1}}dx+\int_1^\infty\frac{\arctan x}{x^{\log x+1}}dx\end{eqnarray*}$$ Replace $x\to\dfrac{1}{x}$ in the second term ,then since $\arctan\frac{1}{x}=\frac{\pi}{2}-\arctan x$ , $$I=\frac{\pi}{2}\int_0^1\frac{dx}{x^{\log x+1}}$$ Substitute $x=e^{-y}$, we have $$I=\frac{\pi}{2}\int_0^\infty e^{-y^2}dy$$ Therefore, $$\int_0^\infty\frac{\arctan x}{x^{\log x+1}}dx=\frac{\pi^{\frac{3}{2}}}{4}$$

$$I=\int_0^\infty\left(\frac{1}{2}-\frac{1}{x}+\frac{1}{e^x-1}\right)\frac{e^{-x}}{x}dx$$ Binet's first formula: $$\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi+\int_0^\infty\left(\frac{1}{e^t-1}-\frac{1}{t}+\frac{1}{2}\right)e^{-zt}\frac{dt}{t}$$ Substitute $z=1$, we obtain $$0=-1+\frac{1}{2}\log2\pi+I$$ Hence, $$I=1-\frac{1}{2}\log2\pi$$

Proof of Binet's first formula:

2022年3月1日 【γ16】ビネの第1公式（導出が技巧的！）

Another solution: $$I=\int_0^\infty\left(\frac{1}{2}-\frac{1}{x}+\frac{1}{e^x-1}\right)\frac{e^{-x}}{x}dx$$

Define $\mu(x)$ in $x>0$ by $$\mu(x)\equiv\log\G(x)-\left(x-\frac{1}{2}\right)\log x+x-\frac{1}{2}\log2\pi$$ We can see below easily $$\mu(x)-\mu(x+1)=\left(x+\frac{1}{2}\right)\log\left(1-\frac{1}{x+1}\right)+1$$ Using $\log(1-X)=-X-\frac{X^2}{2}-\frac{X^3}{3}-\cdots$, we have $$\begin{eqnarray*}\mu(x)-\mu(x+1)&&=\sum_{n=1}^\infty\frac{2x+1}{2n(x+1)^n}-1\\&&=\sum_{n=1}^\infty\left(\frac{1}{n(x+1)^{n-1}}-\frac{1}{2n(x+1)^n}\right)\\&&=\frac{1}{2}\sum_{n=1}^\infty\frac{n}{(n+1)(n+2)(x+1)^{n+1}}\end{eqnarray*}$$ Take the sum of $x$ , $x+1$ , $x+2$ , $\cdots, x+N-1$ and use $\lim_{N\to\infty}\mu(x+N)=0$, we get $$\begin{eqnarray*}\mu(x)&&=\frac{1}{2}\sum_{n=1}^\infty\left[\frac{n}{(n+1)(n+2)}\sum_{k=0}^{\infty}\frac{1}{(x+k+1)^{n+1}}\right]\\&&=\frac{1}{2}\sum_{n=1}^\infty\left[\frac{n}{(n+1)(n+2)}\frac{1}{n!}\sum_{k=0}^{\infty}\int_0^\infty t^ne^{-(x+k+1)t}dt\right]\\&&=\frac{1}{2}\sum_{n=1}^\infty\left[\left(\frac{2}{n+2}-\frac{1}{n+1}\right)\frac{1}{n!}\int_0^\infty e^{-xt}\frac{t^n}{e^t-1}dt\right]\\&&=\frac{1}{2}\int_0^\infty\left[\frac{2}{t^2}\sum_{n=0}^\infty\frac{t^{n+2}}{n!(n+2)}-\frac{1}{t}\sum_{n=0}^\infty\frac{t^{n+1}}{(n+1)!}\right]\frac{e^{-xt}dt}{e^t-1}\\&&=\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)\frac{e^{-xt}}{t}dt\end{eqnarray*}$$ Hence, $$I=\mu(1)=1-\frac{1}{2}\log2\pi$$

detailed text here:

2022年3月8日 「ビネの関数」の第1展開とビネの第1公式（ガンマ関数）

$$\begin{eqnarray*}I&&=\int_0^\infty\frac{xdx}{\sqrt[3]{(e^{3x}-1)^2}}\\&&=-\frac{1}{9}\int_0^1t^{-\frac{1}{3}}(1-t)^{-\frac{2}{3}}\log tdt\quad(e^{-3x}=t)\\&&=-\frac{1}{9}\left.\dd{B(x,y)}{x}\right|_{x=\frac{2}{3},y=\frac{1}{3}}\\&&=-\frac{1}{9}B\left(\frac{2}{3},\frac{1}{3}\right)\left[\psi\left(\frac{2}{3}\right)-\psi(1)\right]\\&&=-\frac{1}{9}\frac{\pi}{\sin\frac{\pi}{3}}\left(-\g-\frac{3}{2}\log3+\frac{\pi}{2\sqrt{3}}+\g\right)\\&&=\frac{\pi}{3\sqrt{3}}\left(\log 3-\frac{\pi}{3\sqrt{3}}\right)\end{eqnarray*}$$

About $\psi(2/3)$:

2022年2月17日 【γ9】ディガンマ関数の相反公式・倍数公式と特殊値・ゼータ関数（ガンマ関数の基礎シリーズ9）

About the derivative of the beta function:

2021年11月29日 ∫logsin xdx 対数正弦積分その1

$$I=\int_0^\infty\frac{x}{(e^x-1)^\frac{2}{3}}dx$$

2022年4月17日 指数関数を含む積分演習 ： 3F2(1)型の超幾何級数とトマエの関係式

Thanks to @BenriBot_ccbs. He told me about an amazing substitution! $$I\equiv \int_0^1\frac{\arctan x}{\sqrt{x(1-x^2)}}dx$$ Substituting $x\to\frac{1-x}{1+x}$, we have $$I=\int_0^1\frac{\arctan\frac{1-x}{1+x}}{\sqrt{x(1-x^2)}}dx$$ Adding these two $I$s, $$\begin{eqnarray*}2I&&=\int_0^1\frac{\arctan x+\arctan\frac{1-x}{1+x}}{\sqrt{x(1-x^2)}}dx\\&&=\int_0^1\frac{\frac{\pi}{4}}{\sqrt{x(1-x^2)}}dx\end{eqnarray*}$$ Hence, $$\begin{eqnarray*}I&&=\frac{\pi}{8}\int_0^1\frac{dx}{\sqrt{x(1-x^2)}}\\&&=\frac{\pi}{16}\int_0^1y^{-\frac{3}{4}}(1-y)^{-\frac{1}{2}}dy\quad(x=\sqrt{y})\\&&=\frac{\pi}{16}B\left(\frac{1}{4},\frac{1}{2}\right)\\&&=\frac{\pi}{16}\frac{\sqrt{\pi}\G(\frac{1}{4})}{\G(\frac{3}{4})}\\&&=\frac{\sqrt{2\pi}\G^2(\frac{1}{4})}{32}\end{eqnarray*}$$