参考過去記事
連続関数 $f(x)$ , $g(x)$ の和 $h(x)\equiv f(x)+g(x)$ は連続関数である。
連続関数 $f(x)$ , $g(x)$ の積 $h(x)\equiv f(x)g(x)$ は連続関数である。
もくじ
関数 $f(x)$ が $x=a$ で連続であるとはこういうことです。
任意の $\epsilon>0$ に対してある $\delta>0$ が存在し$$|x-a|<\delta \Longrightarrow |f(x)-f(a)|<\epsilon$$とできる.
$f(x)=x^2$ や $f(x)=x$ は連続です。これらと同様に $f(x)=x^2+3x$ などでも証明可能ですが、個別にいちいち証明せずとも以下がいえると楽ではないでしょうか。
連続関数 $f(x)$ , $g(x)$ の和 $h(x)\equiv f(x)+g(x)$ は連続関数である。
直感的に「そりゃそうだろう」という感じもしますが、ε-δ論法でちゃんとやってみようと思います。
$f(x)$ と $g(x)$ が連続であることから、前提として以下のことがいえます。
| (1) | 任意の $\epsilon>0$ に対してある $\delta_1>0$ が存在して$$|x-a|<\delta_1 \Rightarrow |f(x)-f(a)|<\frac{\epsilon}{2}$$とできる。 |
| (2) | 任意の $\epsilon>0$ に対してある $\delta_2>0$ が存在して$$|x-a|<\delta_2 \Rightarrow |g(x)-g(a)|<\frac{\epsilon}{2}$$とできる。 |
$\delta$ は $\epsilon$ に依存します。$f(x)$ と $g(x)$ は別の関数ですから $\delta$ の依存の仕方も一般に異なります。なので上記(1)(2)ではそれを明示するために $\delta_1$ , $\delta_2$ としています。
あと変なところといえば式中の $\epsilon/2$ です。もともとここは単なる $\epsilon$ のはずですから違和感があるかもしれません。しかし任意の $\epsilon$ に対して $|f(x)-f(a)|<\epsilon$ と押さえられるなら当然 $|f(x)-f(a)|<\frac{\epsilon}{2}$ となる $\delta$ もとれるはずです($\delta$ をより小さくする)。
このあたりはあとで具体例をやって示してみたいと思います。
さて、(1)(2)から次のことがいえます。
(3) 任意の $\epsilon>0$ に対して $\delta=\min\{\delta_1,\delta_2\}$ ととると
\begin{eqnarray*}&&|x-a|<\delta\\&\Rightarrow& |f(x)-f(a)|<\frac{\epsilon}{2}\;かつ\;|g(x)-g(a)|<\frac{\epsilon}{2}\end{eqnarray*}
とできる。
$\delta\le\delta_1$ かつ $\delta\le\delta_2$ ですから $f(x)$ と $g(x)$ の両方で押さえることができているはずですね。 (3)はそういうことを言っています。
ではいよいよ $h(x)=f(x)+g(x)$ の連続性についてです。任意の $\epsilon>0$ に対して $\delta=\min\{\delta_1,\delta_2\}$ ととると、上記(3)より\begin{eqnarray*}|h(x)-h(a)|&=&|f(x)+g(x)-f(a)-g(a)|\\&\le& |f(x)-f(a)|+|g(x)-g(a)| \\&<&\frac{\epsilon}{2}+\frac{\epsilon}{2}\\&=&\epsilon\end{eqnarray*}
よって $h(x)$ も連続です!
あまり抽象的ではピンとこない感じもするのでもっと具体的にやってみます。
連続関数 $f(x)=x^2$ , $g(x)=x$ の和 $h(x)\equiv f(x)+g(x)$ は連続関数である。
$h(x)=x^2+x$ で直接連続性を示すのもOKですが、本記事の目的はあくまで連続関数の和という観点で理解することです。やってみましょう。二次関数での $\delta$ の取り方については冒頭の過去記事を参照ください。
(1) 任意の $\epsilon>0$ に対して $\delta_1=\sqrt{\displaystyle\frac{\epsilon}{2}+|a|^2}-|a|$ とすると
$$\delta^2_1+2|a|\delta_1=\frac{\epsilon}{2}$$
よって $|x-a|<\delta_1$ ならば\begin{eqnarray*}|f(x)-f(a)|&=&|x-a||x+a|\\&=&|x-a||x-a+2a|\\&\le& |x-a|(|x-a|+2|a|)\\&<&\delta^2_1+2|a|\delta_1\\&=&\frac{\epsilon}{2}\end{eqnarray*}
(2) 任意の $\epsilon>0$ に対して $\delta_2=\displaystyle\frac{\epsilon}{2}$ とすると、$|x-a|<\delta_2$ ならば\begin{eqnarray*}|g(x)-g(a)|&=&|x-a|\\&<&\delta_2\\&=&\displaystyle\frac{\epsilon}{2}\end{eqnarray*}
(3) 任意の $\epsilon>0$ に対して $\delta=\min\{\delta_1,\delta_2\}$ ととると(1)(2)より$$|x-a|<\delta\le\delta_1\Rightarrow|f(x)-f(a)|<\frac{\epsilon}{2}$$$$|x-a|<\delta\le\delta_2\Rightarrow|g(x)-g(a)|<\frac{\epsilon}{2}$$が同時に成り立ちます。
以上より、任意の $\epsilon>0$ に対して $\delta=\min\{\delta_1,\delta_2\}$ ととると(3)より\begin{eqnarray*}|h(x)-h(a)|&=&|f(x)+g(x)-f(a)-g(a)|\\&\le& |f(x)-f(a)|+|g(x)-g(a)| \\&<&\frac{\epsilon}{2}+\frac{\epsilon}{2}\\&=&\epsilon\end{eqnarray*}よって $h(x)$ も連続となります。
(1)(2)は無駄に長い前置きとなりましたが、 $\epsilon$ で押さえられる連続関数に対してはちゃんと $\epsilon/2$ でも押さえられることを確認できました。
例えば $f(x)=\sin x$ と $g(x)=x$ がそれぞれ連続であることが示せたとして、連続関数の積 $f(x)g(x)$ が連続であることが分かっていればわざわざ $x\sin x$ の連続性を個別に証明する必要はありません。というわけで次は
連続関数 $f(x)$ , $g(x)$ の積 $h(x)\equiv f(x)g(x)$ は連続関数である。
これを示したいと思います。
\begin{eqnarray*}|h(x)-h(a)|&=&|f(x)g(x)-f(a)g(a)|\\&=& |f(x)\{g(x)-g(a)\}+g(a)\{f(x)-f(a)\}|\\&\le& |f(x)||g(x)-g(a)|+|g(a)||f(x)-f(a)|\end{eqnarray*}$|f(x)|$ を如何に押さえようか。そもそも $f(x)$ は連続関数ですから「任意の $\epsilon$ に対してある $\delta$ が存在して云々」なのであえて特定の $\epsilon$ をとって以下も言えるはずです。
$\epsilon=|f(a)|$ に対してある $\delta_0$ が存在して$$|x-a|<\delta_0 \Rightarrow |f(x)-f(a)|<|f(a)|$$
そして右側の式を変形すると$$|x-a|<\delta_0 \Rightarrow |f(x)|<2|f(a)|$$この $\epsilon$ は$1$や$2$のような適当な定数でやってみても構いません。とにかく$|f(x)|$ を押さえる式が作れればよいです。
さて、これを代入すると\begin{eqnarray*}|h(x)-h(a)|&\le& |f(x)||g(x)-g(a)|+|g(a)||f(x)-f(a)|\\&<& 2|f(a)||g(x)-g(a)|+|g(a)||f(x)-f(a)|\end{eqnarray*}$|g(x)-g(a)|$ と $|f(x)-f(a)|$ についている係数は定数ですから、この式がうまく $\epsilon$ で押さえられるようにするのはそう難しくありません。押さえるために次の(1)(2)を確認します。
(1) $f(x)$ が連続であることから、任意の $\epsilon$ に対してある $\delta_1$ が存在して$$|x-a|<\delta_1 \Rightarrow |f(x)-f(a)|<\frac{\epsilon}{2|g(a)|}$$が成立する。
そもそも $\epsilon$ は全く任意の正数なのですから $\displaystyle\frac{\epsilon}{2|g(a)|}$ に対しても適切な $\delta$ があるはずですから。
(2) $g(x)$ が連続であることから、任意の $\epsilon$ に対してある $\delta_2$ が存在して$$|x-a|<\delta_2 \Rightarrow |g(x)-g(a)|<\frac{\epsilon}{4|f(a)|}$$が成立する。
そして(1)(2)が成り立つなら\begin{eqnarray*}|h(x)-h(a)|&<& 2|f(a)||g(x)-g(a)|+|g(a)||f(x)-f(a)|\\&<&2|f(a)|\frac{\epsilon}{4|f(a)|}+|g(a)|\frac{\epsilon}{2|g(a)|}\\&=&\epsilon\end{eqnarray*}でうまくいきそうです。
以上のように考えれば、結局次のような証明を与えることができます。
まず $f(x)$ は連続関数より、ある $\delta_0$ が存在して$$|x-a|<\delta_0 \Rightarrow |f(x)-f(a)|<|f(a)|$$すなわち$$|x-a|<\delta_0 \Rightarrow |f(x)|<2|f(a)|$$とできる。
また任意の $\epsilon$ に対してある $\delta_1$ が存在して$$|x-a|<\delta_1 \Rightarrow |f(x)-f(a)|<\frac{\epsilon}{2|g(a)|}$$が成立する。
次に $g(x)$ が連続であることから、任意の $\epsilon$ に対してある $\delta_2$ が存在して$$|x-a|<\delta_2 \Rightarrow |g(x)-g(a)|<\frac{\epsilon}{4|f(a)|}$$が成立する。
よって任意の $\epsilon$ に対して $\delta=\min\{\delta_0,\delta_1,\delta_2\}$ ととると以下のすべてが成り立つ。$$|x-a|<\delta\le\delta_0 \Rightarrow |f(x)|<2|f(a)|$$$$|x-a|<\delta\le\delta_1 \Rightarrow |f(x)-f(a)|<\frac{\epsilon}{2|g(a)|}$$$$|x-a|<\delta\le\delta_2 \Rightarrow |g(x)-g(a)|<\frac{\epsilon}{4|f(a)|}$$従って $|x-a|<\delta$ ならば\begin{eqnarray*}|h(x)-h(a)|&=&|f(x)g(x)-f(a)g(a)|\\&=& |f(x)\{g(x)-g(a)\}+g(a)\{f(x)-f(a)\}|\\&\le& |f(x)||g(x)-g(a)|+|g(a)||f(x)-f(a)|\\&<&2|f(a)|\frac{\epsilon}{4|f(a)|}+|g(a)|\frac{\epsilon}{2|g(a)|}\\&=&\epsilon\end{eqnarray*}
これで連続関数の積 $h(x)$ の連続性が示されました!
関数 $f(x)$ , $g(x)$ が連続なら $f(g(x))$ も連続である。
2つの例を確認したあと,これを証明します.
$f(x)$ と $|\quad|$ の合成関数
連続関数 $f(x)$ について,その絶対値 $|f(x)|$ も連続です.これを示します.まず $f(x)$ は連続関数であることから,連続である区間内の点 $a$ をとると,任意の $\epsilon>0$ に対してある $\delta>0$ が存在して\begin{equation}|x-a|<\delta\Longrightarrow|f(x)-f(a)|<\epsilon\end{equation}が成立します.では $|f(x)|$ はこのときどうかというと三角不等式を用いて\begin{eqnarray*}\bigl||f(x)|-|f(a)|\bigr|&\le&|f(x)-f(a)|\\&<&\epsilon\end{eqnarray*}よって $|f(x)|$ は連続です.
したがって $g(x)=|x|$ とおけば合成関数 $g(f(x))$ も連続であることが分かります.
$f(x)$ と $\sqrt{\quad}$ の合成関数
連続関数 $f(x)$ について,$\sqrt{|f(x)|}$ も連続であることを示します.
$f(a)\neq 0$ なる点 $a$ をとると,任意の $\epsilon>0$ に対してある $\delta_1>0$ が存在して\begin{equation}|x-a|<\delta_1\Longrightarrow|f(x)-f(a)|<\epsilon\sqrt{|f(a)|}\end{equation}が成立します.右辺がちょっと変わってますが,任意の $\epsilon$ でできるなら $\epsilon\sqrt{|f(a)|}$ でも成立するはずです.このとき\begin{eqnarray*}\left|\sqrt{|f(x)|}-\sqrt{|f(a)|}\right|&=&\left|\frac{|f(x)|-|f(a)|}{\sqrt{|f(x)|}+\sqrt{|f(a)|}}\right|\\&\le&\frac{|f(x)-f(a)|}{\sqrt{|f(x)|}+\sqrt{|f(a)|}}\\&\le&\frac{|f(x)-f(a)|}{\sqrt{|f(a)|}}\\&<&\frac{\epsilon\sqrt{|f(a)|}}{\sqrt{|f(a)|}}\\&=&\epsilon\end{eqnarray*}よって連続です.
一方 $f(a)=0$ なる点 $a$ においては, 任意の $\epsilon>0$ に対してある $\delta_2>0$ が存在して\begin{equation}|x-a|<\delta_2\Longrightarrow|f(x)|<\epsilon^2\end{equation}と書くことができます.このとき\begin{eqnarray*}\left|\sqrt{|f(x)|}-\sqrt{|f(a)|}\right|&=&\sqrt{|f(x)|}\\&<&\sqrt{\epsilon^2}=\epsilon\end{eqnarray*}よって $\sqrt{|f(x)|}$ は連続です.
任意の合成関数
では最後に任意の連続関数 $f(x)$ , $g(x)$ の合成関数 $f(g(x))$ の連続性を示します.まず $f(x)$ は連続なので\begin{equation}\forall\epsilon>0,\exists\delta>0,|x-a|<\delta\Rightarrow|f(x)-f(a)|<\epsilon\tag{1}\end{equation}が成立します.次に $g(x)$ については$$\forall\epsilon>0,\exists\delta'>0,|x-a|<\delta'\Rightarrow|g(x)-g(a)|<\epsilon$$なのですが,任意の $\epsilon$ についてこれが言えるということは,上で出てきた $\delta$ としても成立するので次のように書き換えられます.$$\mathrm{上の}\delta\mathrm{に対し},\exists\delta''>0,|x-a|<\delta''\Rightarrow|g(x)-g(a)|<\delta$$(1)と合わせれば\begin{eqnarray*}&&\forall\epsilon>0\, ,\,\exists\delta,\delta''>0\, ,\,|x-a|<\delta''\\&&\Rightarrow|g(x)-g(a)|<\delta\\&&\Rightarrow|f(g(x))-f(g(a))|<\epsilon\end{eqnarray*}
ε論法の記事とか

【2】無限積と級数の関係と収束性

【1】無限積の定義と収束・発散
絶対収束する二重級数・和の順序、コーシー積
正項の二重級数と和の順序
二重数列と二重級数(収束性と足し合わせの順)

実数論の練習問題

無限級数の収束性3(アーベル・ディリクレ)

シュトルツ・チェザロの定理(数列の極限)
【ε論法】極限の計算:limをεδに
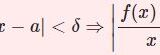
【ε論法】ε-δ論法によって微分する・例題7つ
【ε論法】カントール集合と悪魔の階段の連続性
【ε論法】トマエ関数は有理数の点では不連続

【ε論法】連続関数の和も積も合成も連続関数
【ε論法】一様コーシーな関数列と一様収束性
【ε論法】関数列が一様収束でないことの証明
【ε論法】関数列の各点収束と一様収束
【ε論法】一様連続でないことの証明
【ε論法】関数の一様連続性の証明
【ε論法】関数の連続性とδのテクニック
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。


