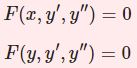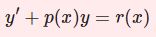今回からオーソドックスな微分方程式を概観していく。まずは１階の方程式からである。１階の線型微分方程式はまず斉次からやるのがいい。その応用として非斉次に取り組もう。前提知識として高校の数学IIIをマスターしておく必要がある。
$y(x)$ に関する微分方程式$$y' +p(x)y=r(x)$$の解法について、斉次（$r(x)=0$）および非斉次（$r(x)\neq 0$）の場合に分けて論じる。
斉次・非斉次は「同次・非同次」ということもあります。
斉次方程式は変数分離により解くことができます。変数分離は非常に強力な武器であり、今回は単純な１階線型の解法として紹介していますが、１階線型でない形でも使えることがあります。微分方程式に出くわしたら、まずはこの方法でできるか試してみるべきです。
斉次１階の方程式を$$\frac{dy}{dx}+p(x)y=0 \Longrightarrow \frac{dy}{y}=-p(x)dx$$と変形すると左辺は $y$ だけ、右辺は $x$ だけになっています。これを変数分離といいます。両辺を積分すれば$$\int\frac{dy}{y}=-\int p(x)dx\Longrightarrow \log y=-\int p(x)dx+C'$$本来右辺も積分してから積分定数を書けばいいのですが、積分結果を書きようがないので積分したものとして定数を書いています。定数をあらためて $C=e^{C'}$ と置きなおせば$$y=Ce^{-\int p(x)dx}$$という結果が得られます。これを一般解といいます。
初期値が与えられている場合、定数が具体的な数値で記述可能です。$y=y(x)$ と書くようにすれば例えば $y(2)=1$ のように初期値が与えられます。
$y'-3x^2y=0$ を解け．
変数分離により$$\frac{dy}{y}=3x^2dx$$両辺を積分して$$\log y=x^3+C'$$ちなみに両辺を積分すると両辺ともに積分定数が出てきますが、右辺にまとめて書いても同じことです。定数をさらに置きなおして$$y=Ce^{x^3}$$となります。これが求める一般解です。
再度になりますが、微分方程式は特に初期条件がなければすべての解を包括して「一般解」として表す必要があります。１階の場合は１つの定数が必要です。今のケースでは $y= e^{x^3} $ , $y= 2e^{x^3} $, $y= 3e^{x^3} $ なども解であり、すべて表すには定数 $C$ がいると分かります。
$e^xy'=3(x+1)y$ を初期値 $y(1)=1$ として解け．
$$\frac{dy}{y}=3e^{-x}(x+1)dx$$となりますので$$\log y=3\int e^{-x}(x+1)dx=-3e^{-x}(x+2)+C'$$よって$$y=C\exp\left[-\frac{3(x+2)}{e^{x}}\right]$$初期条件は $x=1$ のときに $y=1$ なので$$1=C\exp\left[-\frac{9}{e}\right]\Longleftrightarrow C=\exp(9/e)$$$$\therefore\quad y=\exp\left[\frac{9}{e}-\frac{3(x+2)}{e^{x}}\right]$$
初学の場合、これらの例題を解くときに $$y=Ce^{-\int p(x)dx}$$を「公式」として覚えて代入しないほうがいいです。公式に代入するのではなく、公式を導いた方法をたどってしみこませるのが大切だと思います。エッセンスは「変数分離」できるようになることです。
非斉次１階線型微分方程式は$$y' +p(x)y=r(x)\neq 0$$と表されます。どのように解くのでしょう。
上式の両辺に $e^{\int p(x)dx}$ をかけると$$y'e^{\int p(x)dx}+p(x)ye^{\int p(x)dx}=r(x)e^{\int p(x)dx}$$左辺は$$y'e^{\int p(x)dx}+p(x)ye^{\int p(x)dx}=\frac{d}{dx}\left(ye^{\int p(x)dx}\right)$$と変形できるので$$\frac{d}{dx}\left(ye^{\int p(x)dx}\right)=r(x)e^{\int p(x)dx}$$$x$ で積分して$$ye^{\int p(x)dx}=\int r(x)e^{\int p(x)dx}dx$$右辺に積分定数をあえて明示すると、求める解は$$y=e^{-\int p(x)dx}\left[\int r(x)e^{\int p(x)dx}dx+C\right]$$となります。前節と見比べると分かりますが、この解は $r(x)=0$ の場合も成り立ちますので、斉次非斉次を問わず成立するといえます。
もう少し踏み込むと、この解は「斉次方程式の一般解に別の特殊解を加えたもの」として解釈できます。どういうことかというと、斉次 $r=0$ のときは先ほど見たように一般解は $ y_1=Ce^{-\int p(x)dx} $ でしたが、今の場合はこの $y_1$ を用いて$$y=y_1+e^{-\int p(x)dx}\int r(x)e^{\int p(x)dx}dx$$と書けます。第2項は定数 $C=0$ における解です。よって第2項もそれ自体が解ですが $C=0$ という特殊な条件下における解なので「特殊解」といいます。よって非斉次の一般解 $y$ は「斉次方程式の一般解 $y_1$ に別の特殊解を加えたもの」といえるのです。
$xy'=2y+x^3e^x$ を解け．
変形して$$y'-\frac{2}{x}y=x^2e^x$$両辺に $e^{\int p(x)dx}$ をかければいいのですが、天から降りてきた感じがするのであえて回り道してみます。両辺に何をかけるべきか？「左辺をたった１つの項の１階微分にする」ために $y\cdot X$ の微分を考えてみます。$$\frac{d}{dx}(yX)=yX'+y'X\Longrightarrow X^{-1}\frac{d}{dx}(yX)=y'+y\frac{X'}{X}$$元の微分方程式と見比べると$X'/X=-2/x$ とすればよく、その結果 $X=x^{-2}$ となります。従って$$x^2\frac{d}{dx}(yx^{-2})=y'-\frac{2}{x}y$$なる変形が発見できました。これを利用します。$$x^2\frac{d}{dx}(yx^{-2})=x^2e^x \Longrightarrow\frac{d}{dx}(yx^{-2})=e^x$$積分して$$yx^{-2}=e^x+C$$$$\therefore\quad y=x^2(e^x+C)$$これが求める一般解です。
$y'+y\tan x=\sin 2x \: ,\: y(0)=1$ を解け。
$p(x)=\tan x$ に対応するので$$\int p(x)dx=\int\tan xdx=-\log \cos x$$これより $e^{-\log \cos x}=\sec x$ を方程式の両辺にかけます（上の積分に積分定数 $C$ をつけても、$e^C$ はこの後すぐに消去可能なので、無視）。$$y' \sec x +y\tan x \sec x =\sec x\sin 2x \Longleftrightarrow \left( y\sec x \right)^\prime =\sec x\sin 2x=2\sin x$$最後の等号は倍角の公式によります。
積分して$$y\sec x=2\int\sin xdx=-2\cos x+c$$初期条件を考慮すれば $c=3$ となりますので、最終的な解は$$y(x)=-2\cos^2 x+3\cos x$$
$y'+4y=\cos x$ を解け．
次回は、あるタイプの非線型方程式を今回学んだタイプの方程式に帰着して解く手法を取り上げます。
【D2】ベルヌーイの微分方程式
下の記事で物理に応用しています。
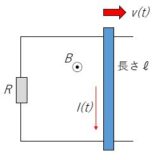磁場を横切る導体棒の運動と微分方程式
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
常微分シリーズの記事一覧はこちら
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
