\begin{equation}x^2y^{\prime\prime}+xy'+(x^2-\nu^2)y=0 \quad (\nu \in \mathbb{R})\tag{1}\end{equation}
初等的に解くことはできませんので級数解を求めます.$x=0$ で正則でないのでフロベニウス法を用いましょう.
フロベニウス法については
 【D11】級数法・フロベニウス法
【D11】級数法・フロベニウス法
を参照ください.
もくじ
$$y(x)=\sum^\infty_{m=0}a_mx^{m+r}\;,\;a_0\ne 0$$とおき,微分方程式(1)に代入します.\begin{eqnarray*}&&x^2y^{\prime\prime}+xy'+(x^2-\nu^2)y=0\\&\Leftrightarrow& \sum^\infty_{m=0}(m+r)(m+r-1)a_mx^{m+r}+\sum^\infty_{m=0}(m+r)a_mx^{m+r}+(x^2-\nu^2)\sum^\infty_{m=0}a_mx^{m+r}=0 \\&\Leftrightarrow& \sum^\infty_{m=0}\{(m+r)(m+r-1)+(m+r)-\nu^2\}a_mx^m+ \sum^\infty_{m=2}a_{m-2}x^m=0\\&\Leftrightarrow& (r^2-\nu^2)a_0+(1+r+\nu)(1+r-\nu)a_1x+\sum^\infty_{m=2}\{(m+r+\nu)(m+r-\nu)a_m+a_{m-2}\}x^m=0\end{eqnarray*}第1項に注目します.決定方程式は $a_0\ne 0$ より $r^2-\nu^2=0$ で,その解は $r=\pm\nu$ です.それぞれの $r$ について求めた級数が特殊解になります.なお(1)の形からして $\nu\ge 0$ として一般性を失いません.
$\nu\notin \mathbb{Z}$ とします.$r=\nu \geq 0$ のほうから考えます.級数を代入した微分方程式は$$(1+2\nu)a_1x+\sum^\infty_{m=0}\{m(m+2\nu)a_m+a_{m-2}\}x^m=0$$これが恒等的に成り立つことにより得られる漸化式は$$\begin{cases}a_0= 任意\\a_1=0\\m(m+2\nu)a_m+a_{m-2}=0\end{cases}$$よって奇数項はすべて$0$であり,偶数項のみ考えればよいです.\begin{eqnarray*}a_{2m}&=&-\frac{1}{2m(2m+2\nu)}a_{2m-2}\\&\vdots &\\&=&\left(-\frac{1}{4}\right)^m\frac{\Gamma(\nu+1)}{m! \Gamma(m+\nu+1)}a_0\end{eqnarray*}$a_0=\displaystyle\frac{1}{2^\nu \Gamma(\nu+1)}$ とすると$$a_{2m}=\left(-\frac{1}{4}\right)^m\frac{1}{2^\nu m!\Gamma(m+\nu+1)}$$これによって特殊解の1つ\begin{equation}J_\nu(x) = \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m+\nu}\tag{2}\end{equation}が求まります.$J_\nu(x)$ を第1種ベッセル関数といいます。$\nu$ は微分方程式(1)において $\nu^2$ としてあらわれているため,$r=-\nu$とした場合も同時に解ですから,そのときの特殊解は\begin{equation}J_{-\nu}(x) =\sum^\infty_{m=0}\frac{(-1)^m}{2^{2m-\nu}m! \Gamma(m-\nu+1)}x^{2m-\nu}\tag{3}\end{equation}です.
よって $J_\nu(x)$ と $J_{-\nu}(x)$ の2つの特殊解を得ることができました.これらは独立であり,一般解は即座に$$y(x)=c_1J_\nu(x) +c_2 J_{-\nu}(x)$$とできます.
$\nu$ が非負整数 $n$ であるとします.決定方程式の解は $r=\pm n$ です.$r=n$ のときは(2)そのままの式 $J_n(x)$ が特殊解となります.\begin{equation}J_n(x)= \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+n}m!(m+n)!}x^{2m+n}\tag{4}\end{equation}
$r=-n$ のときは漸化式$$\begin{cases}a_0= 任意\\a_1=0\\m(m-2n)a_m+a_{m-2}=0\end{cases}$$ を得ます.奇数項はすべてゼロになるので 偶数項についての漸化式$$ 2m(2m-2n)a_{2m}+a_{2m-2}=0 $$を考えます.$m=n$ としてみると $a_{2n-2}=0$ となります.よって漸化式を繰り返し用いることにより$$a_0=a_2=\cdots=a_{2n-2}=0$$となりますので $a_{2n}$ が任意の数で開始項となります.(3)と一致するようにとれば$$ J_{-n}(x) =\sum^\infty_{m=n}\frac{(-1)^m}{2^{2m-n}m! (m-n)!}x^{2m-n} $$$m=n$ スタートであることに注意.これを変形していくと\begin{eqnarray*}J_{-n}(x)&=& \sum^\infty_{m=0}\frac{(-1)^{m+n}}{2^{2m+n}(m+n)! m!}x^{2m+n}\\&=& (-1)^n\sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+n}(m+n)! m!}x^{2m+n}\\&=&(-1)^nJ_n(x)\end{eqnarray*}よって $J_n(x)$ と $J_{-n}(x)$ は一次従属です. この2つの特殊解は一般解を与えないことになります.
では $\nu\in\mathbb{Z}$ のときの一般解はどうすればいいのでしょう.
まず $\nu=0$ で考えます.\begin{equation}xy^{\prime\prime}+y'+xy=0\end{equation}フロベニウス法によって得られる $J_0(x)$ が1つ目の特殊解になります.よって\begin{equation}xJ^{\prime\prime}_0+J'_0+xJ_0=0\end{equation}が成り立ちます.ここまでは今までと変わりありません.
ここで第2の特殊解の試行解として$$y_2=J_0(x)\ln x+\sum^\infty_{m=1}A_mx^m$$と置き,微分方程式に代入してみると$$(xJ^{\prime\prime}_0+J'_0+xJ_0)\ln x+2J_0'+\sum^\infty_{m=1}m^2A_mx^{m-1}+\sum^\infty_{m=3}A_{m-2}x^{m-1}=0$$第1項は消えて$$2J_0'+\sum^\infty_{m=1}m^2A_mx^{m-1}+\sum^\infty_{m=3}A_{m-2}x^{m-1}=0$$これに第1種ベッセル関数の式$$J_0(x) = \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m}m! m!}x^{2m}$$を代入すると$$\sum^\infty_{m=1}\frac{(-1)^m}{2^{2m-2}m! (m-1)!}x^{2m-1}+\sum^\infty_{m=1}m^2A_mx^{m-1}+\sum^\infty_{m=3}A_{m-2}x^{m-1}=0$$シグマを書き下して次数の低いほうから調べていくと、
- 定数項から $A_1=0$
- 1次の項から $4A_2-1=0$
- $x^{2k}$ の項から $(2k+1)^2A_{2k+1}+A_{2k-1}=0\;(k\ge1 )$
- $x^{2k-1}$ の項から$$\frac{(-1)^k}{2^{2k-2}k!(k-1)!}+4k^2A_{2k}+A_{2k-2}=0\;(k\ge 2)$$
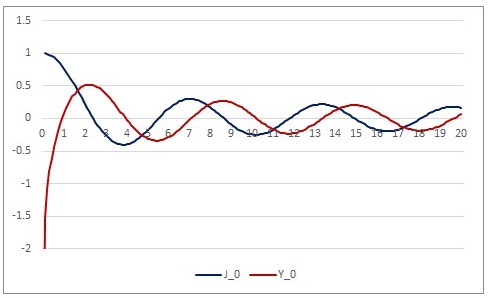
よって以下の関係式を得ます。$$\begin{cases}A_1=A_3=A_5=\cdots =0 \\A_2=\displaystyle\frac{1}{4}\\A_{2k}=\left(-\displaystyle\frac{1}{4k^2}\right)\left[ A_{2k-2}+\displaystyle\frac{(-1)^k}{2^{2k-2}k!(k-1)!}\right]\quad (k\geq 2)\end{cases}$$偶数項の漸化式は解けて$$A_{2k}=\frac{(-1)^{k-1}}{2^{2k}(k!)^2}h_k \quad , \quad h_k=1+\frac{1}{2}+\cdots \frac{1}{k}$$となります(数学的帰納法で簡単に確認できます).よって第2の特殊解は$$y_2=J_0(x)\ln x-\sum^\infty_{m=1}\frac{(-1)^mh_m}{2^{2m}(m!)^2}x^{2m}$$解の基底は $J_0$ とこの $y_2$ としてもよいのですが、$y_2$ を $\displaystyle\frac{2}{\pi}(y_2+(\gamma-\ln 2)J_0)$ におきかえて基底としたものを0次の第2種ベッセル関数 $Y_0(x)$ とよび,$$Y_0(x)=\frac{2}{\pi}\left[ J_0(x)\left(\ln\frac{x}{2}+\gamma \right)- \sum^\infty_{m=1}\frac{(-1)^mh_m}{2^{2m}(m!)^2}x^{2m} \right]$$となります。$\gamma$ はオイラー・マスケローニ定数です。
よって $\nu=0$ のベッセルの微分方程式の一般解は$$y=c_1J_0(x)+c_2Y_0(x)$$と表せることが分かります.第1種ベッセル関数と第2種ベッセル関数の線型結合が一般解となるわけです.
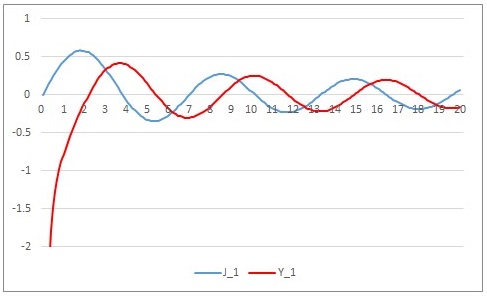
なお一般の $n$ における第2種ベッセル関数 $Y_n(x)$ は$$Y_n(x)=\frac{2}{\pi}J_n(x)\left(\ln\frac{x}{2}+\gamma\right)-\frac{x^n}{\pi}\sum^\infty_{m=0}\frac{(-1)^m(h_m+h_{m+n})}{2^{2m+n}m!(m+n!)}x^{2m}-\frac{x^{-n}}{\pi}\sum^{n-1}_{m=0}\frac{(n-m-1)!}{2^{2m-n}m!}x^{2m}$$となります.これの導出については:
一般の $\nu\in\mathbb{R}$ における第2種ベッセル関数は$$\begin{cases}Y_\nu(x)=\displaystyle\frac{1}{\sin\nu\pi}[J_\nu(x)\cos\nu\pi-J_{-\nu}(x)]\\Y_n(x)=\displaystyle\lim_{\nu\to n}Y_\nu(x)\end{cases}$$$\nu \notin \mathbb{Z}$ のときは解の基底を $J_\nu , J_{-\nu}$ としてきましたが、$Y_\nu$ がそれらの線型結合になっているので基底を $Y_\nu ,J_\nu$ に取り換えても構いませんよね.このようにすることで $\nu \in \mathbb{Z}$ では $Y_\nu$ は $\nu\to n$ の極限値で求まるようになっています.
以上からベッセルの微分方程式の一般解は$$y(x)=c_1J_\nu(x)+c_2Y_\nu(x)$$となるのです.
$$x^\nu J_\nu=\sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m!\Gamma(m+\nu+1)}x^{2m+2\nu}$$を微分すると$$\frac{d}{dx}(x^\nu J_\nu)=\sum^\infty_{m=0}\frac{(-1)^m\cdot 2(m+\nu)}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m+2\nu-1}=x^\nu J_{\nu-1}$$$$\therefore \frac{d}{dx}(x^\nu J_\nu)=x^\nu J_{\nu-1}$$同様にして$$\frac{d}{dx}(x^{-\nu} J_\nu)=-x^{-\nu} J_{\nu+1}$$あらわれた2式をそれぞれ微分して$$\begin{cases}\nu x^{\nu-1}J_\nu +x^\nu {J_\nu}'=x^\nu J_{\nu-1} \\-\nu x^{-\nu-1}J_\nu +x^{-\nu} {J_\nu}'=-x^{-\nu} J_{\nu+1}\end{cases}$$この2式から${J_\nu}'$を消去あるいは$J_\nu$を消去することで$$J_{\nu+1}+J_{\nu-1}=\frac{2\nu}{x}J_\nu$$$$J_{\nu-1}-J_{\nu+1}=2{J_\nu}'$$なる漸化式を得ます.
第1種ベッセル関数 $J_\nu$ は特殊関数であり,一般には初等関数で表せません.しかし $\nu$ が半整数値の場合は特別です.第1種ベッセル関数の式$$J_\nu(x) = \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m+\nu}$$より\begin{eqnarray*}J_{1/2}(x)&=&\sqrt{x}\sum^\infty_{m=0}\frac{(-1)^m x^{2m}}{2^{2m+1/2}m!\Gamma(m+3/2)}\\ &=&\frac{1}{\sqrt{x}}\sum^\infty_{m=0}\frac{(-1)^m x^{2m+1}}{2^{2m+1/2}m!\Gamma(m+3/2)}\\ &=&\frac{1}{\sqrt{x}}\sum^\infty_{m=0}\frac{(-1)^m x^{2m+1}}{2^{2m+1/2}m!(m+1/2)(m-1/2)\cdots 1/2\Gamma(1/2)}\\ &=&\sqrt{\frac{2}{\pi x}}\sum^\infty_{m=0}\frac{(-1)^m x^{2m+1}}{2^{2m+1}m!(m+1/2)(m-1/2)\cdots 1/2}\\ &=& \sqrt{\frac{2}{\pi x}}\sum^\infty_{m=0}\frac{(-1)^m x^{2m+1}}{(2m)!!(2m+1)!!}\\ &=& \sqrt{\frac{2}{\pi x}}\sum^\infty_{m=0}\frac{(-1)^m x^{2m+1}}{(2m+1)!}\\ &=&\sqrt{\frac{2}{\pi x}}\sin x\end{eqnarray*}と計算でき,初等関数だと分かります.
漸化式 $(x^{1/2}J_{1/2})'=x^{1/2}J_{-1/2}$ を利用して$$J_{-1/2}(x)=\sqrt{\frac{2}{\pi x}}\cos x$$さらに3項間漸化式$$J_{\nu+1}+J_{\nu-1}=\frac{2\nu}{x}J_\nu$$を用いれば $J_{3/2}$ も初等関数であり,繰り返し漸化式を使うことで $\nu=\pm \displaystyle\frac{1}{2} , \pm\frac{3}{2},\cdots$ で $J_\nu$ は初等函数であらわせることが分かります.
$$x^2y^{\prime\prime}+xy'+\left(x^2-\displaystyle\frac{1}{9}\right)y=0$$
$\nu=1/3$ より第1種ベッセル関数が一般解を与えます.$$y=c_1J_{1/3}(x)+c_2J_{-1/3}(x)$$もちろん第2項を $Y_{1/3}(x)$ としてもOK.
$$x^2y^{\prime\prime}+xy'+(a^2x^2-\nu^2)y=0\;(\nu\notin\mathbb{Z})$$
$ax=z$ とおくと$$\frac{dy}{dx}=a\frac{dy}{dz}\;,\;\frac{d^2y}{dx^2}=a^2\frac{d^2y}{dz^2}$$代入して整理すると$$z^2\frac{d^2y}{dz^2}+z\frac{dy}{dz}+(z^2-\nu^2)y=0$$$\nu\notin\mathbb{Z}$ よりベッセル関数が一般解を与えます。$$y=c_1J_\nu(ax)+c_2J_{-\nu}(ax)$$
$$x^2y^{\prime\prime}+xy'+\left(4x^4-\displaystyle\frac{1}{4}\right)y=0$$
$x^2=z$ とおくと $$y'=2\sqrt{z}\frac{dy}{dz}\;,\;y^{\prime\prime}=4z\frac{d^2y}{dz^2}+2\frac{dy}{dz}$$微分方程式に代入して整理すると$$z^2\frac{d^2y}{dz^2}+z\frac{dy}{dz}+\left(z^2-\displaystyle\frac{1}{16}\right)y=0$$$\nu\notin\mathbb{Z}$ よりベッセル関数が一般解を与えます.$$y=c_1J_{1/4}(x^2)+c_2J_{-1/4}(x^2)$$
$xy^{\prime\prime}+5y'+xy=0$ の特殊解を1つ求めよ。
$u(x)=x^2y$ とおくと$$y'=\frac{1}{x^2}u'-\frac{2}{x^3}u$$$$y^{\prime\prime}=\frac{6}{x^4}u-\frac{4}{x^3}u'+\frac{1}{x^2}u^{\prime\prime}$$微分方程式に代入して整理すると$$x^2u^{\prime\prime}+xu'+(x^2-4)=0$$よって特殊解は $u(x)=J_{2}(x)$ ですので$$y_1=\frac{1}{x^2}J_{2}(x)$$
$$x^2y^{\prime\prime}+\displaystyle\frac{1}{4}\left(x+\frac{3}{4}\right)y=0$$
$y=u(x)\sqrt{x}\;,\;\sqrt{x}=z$ と変換すると$$z^2\frac{d^2u}{dz^2}+z\frac{du}{dz}+\left(z^2-\frac{1}{4}\right)u=0$$よって$$u(z)=aJ_{1/2}(z)+bJ_{-1/2}(z)$$ここで$$J_\nu(x) = x^\nu\sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m}$$$$J_{-\nu}(x) = x^{-\nu} \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m-\nu}m! \Gamma(m-\nu+1)}x^{2m}$$より級数を計算すると$$J_{1/2}(z)\propto\frac{\sin z}{\sqrt{z}}\;,\;J_{-1/2}(z)\propto\frac{\cos z}{\sqrt{z}}$$となりますので$$u(z)=c_1\frac{\sin z}{\sqrt{z}}+c_2\frac{\sin z}{\sqrt{z}}$$$$\therefore\quad y(x)=x^{\frac{1}{4}}(c_1\sin\sqrt{x}+c_2\cos\sqrt{x})$$
$I=\displaystyle\int^2_1x^{-3}J_4(x)dx$ を計算せよ.$J_0$ , $J_1$ を解答に含めてよい.
$x^{-3}J_4=-(x^{-3}J_3)'$ より$$I=-\int^2_1(x^{-3}J_3)'dx=-\left[ \frac{J_3(x)}{x^3}\right]^2_1$$となります.ここで$$J_3+J_1=\frac{4}{x}J_2 \Longleftrightarrow J_3=\frac{4}{x}J_2-J_1$$$$J_2+J_0=\frac{2}{x}J_1 \Longleftrightarrow J_2=\frac{2}{x}J_1-J_0$$より$$J_3=\left( \frac{8}{x^2}-1 \right)J_1-\frac{4}{x}J_0$$$$\therefore I=-\frac{1}{8}J_1(2)+\frac{1}{4}J_0(2)+7J_1(1)-4J_0(1)$$
$\displaystyle\frac{d}{dx}(x^\nu J_\nu)=x^\nu J_{\nu-1}\; ,\; \displaystyle\frac{d}{dx}(x^{-\nu} J_\nu)=-x^{-\nu} J_{\nu+1}$ の2式からベッセル微分方程式を導け.
$$\begin{cases}J_{\nu-1}=x^{-\nu}\displaystyle\frac{d}{dx}(x^\nu J_\nu)\\\displaystyle\frac{d}{dx}(x^{-\nu+1} J_{\nu-1})=-x^{-\nu+1}J_{\nu}\end{cases}$$$J_{\nu-1}$を下の式へ代入すれば,\begin{eqnarray*}&&\frac{d}{dx}\left[ x^{-\nu+1} x^{-\nu}\displaystyle\frac{d}{dx}(x^\nu J_\nu)\right]=-x^{-\nu+1} J_{\nu}\\&\Leftrightarrow& \frac{d}{dx}\left[x^{-2\nu+1}(\nu x^{\nu-1}J_\nu+x^\nu J'_\nu)\right]=-x^{-\nu+1} J_{\nu}\\&\Leftrightarrow& x^2J^{\prime\prime}_\nu+xJ'_\nu+(x^2-\nu^2)J_\nu=0\end{eqnarray*}これはまさにベッセルの微分方程式です.
一般の斉次2階線型常微分方程式 $y^{\prime\prime}+p(x)y'+q(x)y=0$ において $y=u(x)v(x)$ としたときに $u'$ を含まないような微分方程式を得たいとします.代入すると$$u^{\prime\prime}v+(2v'+pv)u'+(v^{\prime\prime}+pv')u+quv=0$$$u'$ の項をなくすには $2v'+pv=0$ すなわち$$v(x)=\exp \left(-\frac{1}{2}\int p(x)dx\right)$$とおけばよいことになります.
ベッセルの微分方程式において応用してみましょう.$$x^2y^{\prime\prime}+xy'+(x^2-\nu^2)y=0$$を$$y^{\prime\prime}+\frac{1}{x}y'+\left(1-\frac{\nu^2}{x^2}\right)y=0$$と変形して$$v(x)\equiv\exp \left(-\frac{1}{2}\int \frac{1}{x}dx\right)=\frac{1}{\sqrt{x}}$$とおきます.$y=u(x)\displaystyle\frac{1}{\sqrt{x}}$ とおいてベッセル方程式に代入すると1階微分がない方程式
$$x^2u^{\prime\prime}+\left(x^2+\frac{1}{4}-\nu^2\right)u=0$$
を得ます.
例題をやってみましょう.
$\nu=1/2$ についてのベッセルの微分方程式を上の方法で解け.
$y=u(x)\displaystyle\frac{1}{\sqrt{x}}$ として1階導関数を消去すると$$u^{\prime\prime}+u=0$$すなわち $u(x)=c_1\sin x+c_2\cos x$ です.よって解は$$y=c_1\frac{\sin x}{\sqrt{x}}+c_2\frac{\cos x}{\sqrt{x}}$$
物理学でベッセルの微分方程式はときどき現れます.参考記事は以下です.
第1種ベッセル関数の積分表示についての記事は
ベッセルの微分方程式の非斉次解についてはこちら:
Anger関数とWeber関数②(ベッセル微分方程式の非斉次解)
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。

【Amazon】常微分方程式 (技術者のための高等数学)
次回の記事:
常微分方程式シリーズ
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。




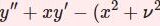
決定方程式を導く、の項の、最後のシグマはm=2ではありませんか?
ありがとうございます。訂正しました。何か見つけたらまたいつでもお願いします。