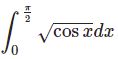関数 $f(x)$ が $x=a$ において微分可能であり,$f'(a)=A$ であることを $\epsilon-\delta$ で表現すると
$$\forall\epsilon>0,\exists\delta>0,|x-a|<\delta\Rightarrow \left|\frac{f(x)-f(a)}{x-a}-A\right|<\epsilon$$が成立するとき,$f(x)$ は $x=a$ で微分可能であり,微分係数は $f'(a)=A$ である.
この定義に沿っていろんな関数の微分を試してみました.なので例題重視の記事となります.
関数 $f(x)=C$ を $x=a$ で微分せよ.
任意の $\epsilon>0$ に対し\begin{eqnarray*}\left|\frac{f(x)-f(a)}{x-a}-0\right|&=&\left|\frac{C-C}{x-a}-0\right|\\&=&0<\epsilon\end{eqnarray*}$$\therefore\;f'(a)=0$$$\delta$ は特に定める必要はありませんでした.
関数 $f(x)=3x$ を $x=a$ で微分せよ.
任意の $\epsilon>0$ に対し\begin{eqnarray*}\left|\frac{f(x)-f(a)}{x-a}-3\right|&=&\left|\frac{3x-3a}{x-a}-3\right|\\&=&0<\epsilon\end{eqnarray*}$$\therefore\;f'(a)=3$$これも $\delta$ を定める必要なしですね.
関数 $f(x)=x^2$ を $x=a$ で微分せよ.
任意の $\epsilon>0$ に対し $\delta=\epsilon$ ととって $|x-a|<\delta$ を仮定すると\begin{eqnarray*}\left|\frac{f(x)-f(a)}{x-a}-2a\right|&=&\left|\frac{x^2-a^2}{x-a}-2a\right|\\&=&|x-a|<\delta=\epsilon\end{eqnarray*}すなわち$$\left|\frac{f(x)-f(a)}{x-a}-2a\right|<\epsilon$$$$\therefore\;f'(a)=2a$$
例題1~3の解答を見ると気づくと思いますが,あらかじめ微分係数が分かっているからすぐに立式できています.微分係数の値は $\epsilon$ 論法を使わずに(高等学校の知識で)分かりますからね.あくまでそれを $\epsilon$ 論法で厳密に証明しなおしたというイメージです.でも次の例題4では微分係数があらかじめ分からないとして考えてみます.
関数 $f(x)=x^3-x$ を $x=1$ で微分せよ.
\begin{eqnarray*}\left|\frac{x^3-x-0}{x-1}-A\right|&=&|x^2+x-A|\\&=&|(x-1)^2+3(x-1)-A+2|\\&=&|x-1|^2+3|x-1|+|A-2|\\&<&\delta^2+3\delta+|A-2|\end{eqnarray*}これを見ると $A=2$ であれば最右辺を$0$に近づけることができます.よって求める微分係数は $f'(1)=2$ と予想されます.$\delta$ の取り方は $\delta^2+3\delta=\epsilon$ を $\delta$ について解いたものをとってもいいのですが,$\delta\le 1$ で抑えて $\delta=\min\{\displaystyle\frac{\epsilon}{4},1\}$ ととるとスマートな感じになります。
ではやっていきます!
任意の $\epsilon>0$ に対し $\delta=\min\{\displaystyle\frac{\epsilon}{4},1\}$ ととって $|x-1|<\delta$ を仮定すると\begin{eqnarray*}\left|\frac{x^3-x-0}{x-1}-2\right|&=&|x^2+x-2|\\&=&|(x-1)^2+3(x-1)|\\&=&|x-1|^2+3|x-1|\\&<&\delta^2+3\delta\\&\le&\delta+3\delta\;(\because\delta\le1)\\&=&4\delta\\&\le&4\frac{\epsilon}{4}=\epsilon\end{eqnarray*}$$\therefore\;f'(1)=2$$
関数 $f(x)=\sqrt{x}$ を $x=a>0$ で微分せよ.
$|x-a|<\delta$ とすると\begin{eqnarray*}\left|\frac{\sqrt{x}-\sqrt{a}}{x-a}-A\right|&=&\left|\frac{1}{\sqrt{x}+\sqrt{a}}-A\right|\\&=&\left|\frac{1}{\sqrt{x}+\sqrt{a}}-\frac{1}{2\sqrt{a}}+\frac{1}{2\sqrt{a}}-A\right|\\&=&\left|\frac{\sqrt{a}-\sqrt{x}}{2\sqrt{a}(\sqrt{x}+\sqrt{a})}+\frac{1}{2\sqrt{a}}-A\right|\\&\le&\frac{|\sqrt{x}-\sqrt{a}|}{2\sqrt{a}(\sqrt{x}+\sqrt{a})}+\left|A-\frac{1}{2\sqrt{a}}\right|\\&=&\frac{|x-a|}{2\sqrt{a}(\sqrt{x}+\sqrt{a})^2}+\left|A-\frac{1}{2\sqrt{a}}\right|\\&\le&\frac{|x-a|}{2\sqrt{a}(0+\sqrt{a})^2}+\left|A-\frac{1}{2\sqrt{a}}\right|\\&=&\frac{|x-a|}{2a\sqrt{a}}+\left|A-\frac{1}{2\sqrt{a}}\right|\\&<&\frac{\delta}{2a\sqrt{a}}+\left|A-\frac{1}{2\sqrt{a}}\right|\end{eqnarray*}これを見ると $A=\displaystyle\frac{1}{2\sqrt{a}}$ であれば最右辺を $0$ に近づけることができます.よって求める微分係数は $f'(a)=\displaystyle\frac{1}{2\sqrt{a}}$ と予想されます.したがって以下のように示すことができます.
関数 $f(x)=\sqrt{x}$ 上の点 $a$ を考える.任意の $\epsilon>0$ に対して $\delta=2a\sqrt{a}\,\epsilon$ ととると,先ほどと同様の計算を進めて\begin{eqnarray*}\left|\frac{\sqrt{x}-\sqrt{a}}{x-a}-\frac{1}{2\sqrt{a}}\right|&\le&\frac{\delta}{2a\sqrt{a}}\\&<&\epsilon\end{eqnarray*}\begin{equation}\therefore\;f'(a)=\frac{1}{2\sqrt{a}}\end{equation}連続性の証明と比べて微分はなかなか面倒ですね.
関数 $f(x)=\displaystyle\frac{1}{x}$ を $x=a$ で微分せよ.
微分係数は $-\displaystyle\frac{1}{a^2}$ だと予想してやってみましょう.
$|x-a|<\delta$ とすると\begin{eqnarray*}\left|\frac{\frac{1}{x}-\frac{1}{a}}{x-a}-\left(-\frac{1}{a^2}\right)\right|&=&\left|\frac{a-x}{ax(x-a)}-\left(-\frac{1}{a^2}\right)\right|\\&=&\left|-\frac{1}{ax}+\frac{1}{a^2}\right|\\&=&\frac{1}{|a|}\left|\frac{1}{a}-\frac{1}{x}\right|\\&=&\frac{1}{|a|}\left|\frac{x-a}{ax}\right|\\&=&\frac{|x-a|}{a^2|x|}\\&<&\frac{\delta}{a^2|x|}\end{eqnarray*}$a$ は定数ですからいいのですが,$x$ が残っているおかげで最右辺を $0$ に近づけることができません.そこで $\delta\le\displaystyle\frac{|a|}{2}$ でおさえてみると $|x-a|<\displaystyle\frac{|a|}{2}$ となります.すると\begin{equation}\bigl||x|-|a|\bigr|\le|x-a|<\displaystyle\frac{|a|}{2}\end{equation}よって $-\displaystyle\frac{|a|}{2}<|x|-|a|<\displaystyle\frac{|a|}{2}$ となるので\begin{equation}\therefore\;\frac{|a|}{2}<|x|<\frac{3|a|}{2}\end{equation}これを用いれば\begin{eqnarray*}\frac{\delta}{a^2|x|}&<&\frac{\delta}{a^2\frac{|a|}{2}}\\&=&\frac{2\delta}{|a|^3}\end{eqnarray*}
ということで以下のように解答できます.
任意の $\epsilon>0$ に対して $\delta=\min\left\{\displaystyle\frac{|a|}{2},\displaystyle\frac{|a|^3}{2}\epsilon\right\}$ ととると,先ほどの議論から以下の2式が成立します.\begin{equation}\delta\le\frac{|a|}{2}\Longrightarrow\frac{|a|}{2}<|x|<\frac{3|a|}{2}\end{equation}\begin{equation}\delta\le\frac{|a|^3}{2}\epsilon\Longrightarrow\frac{2\delta}{|a|^3}\le\epsilon\end{equation}これらを用いて式変形していくと\begin{eqnarray*}\left|\frac{\frac{1}{x}-\frac{1}{a}}{x-a}-\left(-\frac{1}{a^2}\right)\right|&=&\frac{|x-a|}{a^2|x|}\\&<&\frac{\delta}{a^2|x|}\\&<&\frac{2\delta}{|a|^3}\\&\le&\epsilon\end{eqnarray*}\begin{equation}\therefore\;f'(a)=-\frac{1}{a^2}\end{equation}こちらもなかなか大変でした。
関数 $f(x)=\sin x$ を $x=a$ で微分せよ.
本題の前に準備をしておきます.
まず前提知識として次の式を認めます.\begin{equation}\displaystyle\lim_{\theta\to 0}\frac{\sin\theta}{\theta}=1\end{equation}これを $\epsilon-\delta$ で表現すると\begin{equation}\forall\epsilon>0,\exists\delta>0,|\theta|<\delta\Rightarrow\left|\frac{\sin\theta}{\theta}-1\right|<\epsilon\end{equation}微分を考える今の場合 $\delta$ でおさえるのは $|x-a|$ ですので\begin{equation}\forall\epsilon>0,\exists\delta>0,|x-a|<\delta\Rightarrow\left|\frac{\sin(x-a)}{x-a}-1\right|<\epsilon\end{equation}と書き換えておきます.また,この式が任意の $\epsilon>0$ について成り立つなら $\epsilon/2$ と書き直しても成立するはずです.すなわち任意の $\epsilon>0$ に対してある $\delta_1>0$ が存在して\begin{equation}|x-a|<\delta_1\Rightarrow\left|\frac{\sin(x-a)}{x-a}-1\right|<\frac{\epsilon}{2}\tag{1}\end{equation}なぜ分母を$2$にするかという理由は特にありません. のちのちのために $\epsilon$ より小さくしたいだけです.
さてもう1つ先にやることがあります.$|x-a|<\delta_1$ なら 当然 $\left|\displaystyle\frac{x-a}{2}\right|<\delta_1$ なので\begin{equation}\left|\frac{\sin\frac{x-a}{2}}{\frac{x-a}{2}}-1\right|<\frac{\epsilon}{2}\end{equation}これを変形すると\begin{equation}\left|\frac{\sin\frac{x-a}{2}}{\frac{x-a}{2}}\right|^2<\left(1+\frac{\epsilon}{2}\right)^2\tag{2}\end{equation}以上で準備完了です.
任意の $\epsilon>0$ に対して $\delta$ を以下のようにとります.\begin{equation}\delta=\min\left\{\delta_1,\frac{\epsilon}{2(1+\frac{\epsilon}{2})^2}\right\}\tag{3}\end{equation}$\delta_1$ は先ほど出てきたやつです.$|x-a|<\delta$ とすると $\delta\le\delta_1$ ですから式(1)(2)より\begin{equation}\left|\frac{\sin(x-a)}{x-a}-1\right|<\frac{\epsilon}{2}\tag{4}\end{equation}\begin{equation}\left|\frac{\sin\frac{x-a}{2}}{\frac{x-a}{2}}\right|^2<\left(1+\frac{\epsilon}{2}\right)^2\tag{5}\end{equation}が成立します.
では微分を導出していきます.\begin{eqnarray*}&&\left|\frac{\sin x-\sin a}{x-a}-\cos a\right|\\&=&\left|\frac{\sin[(x-a)+a]-\sin a}{x-a}-\cos a\right|\\&=&\left|\frac{\sin(x-a)\cos a+\cos(x-a)\sin a-\sin a}{x-a}-\cos a\right|\\&=&\left|\frac{\cos a\sin(x-a)-\sin a(1-\cos(x-a))}{x-a}-\cos a\right|\\&=&\left|\cos a\left(\frac{\sin(x-a)}{x-a}-1\right)-\sin a\frac{1-\cos(x-a)}{x-a}\right|\\&\le&|\cos a|\left|\frac{\sin(x-a)}{x-a}-1\right|+|\sin a|\left|\frac{1-\cos(x-a)}{x-a}\right|\\&=&|\cos a|\left|\frac{\sin(x-a)}{x-a}-1\right|+\frac{|\sin a|}{2}|x-a|\left|\frac{\sin\frac{x-a}{2}}{\frac{x-a}{2}}\right|^2\\&<&\left|\frac{\sin(x-a)}{x-a}-1\right|+|x-a|\left|\frac{\sin\frac{x-a}{2}}{\frac{x-a}{2}}\right|^2\\&<&\frac{\epsilon}{2}+|x-a|\left|\frac{\sin\frac{x-a}{2}}{\frac{x-a}{2}}\right|^2\;(\because(4))\\&<&\frac{\epsilon}{2}+|x-a|\left(1+\frac{\epsilon}{2}\right)^2\;(\because(5))\\&<&\frac{\epsilon}{2}+\delta\left(1+\frac{\epsilon}{2}\right)^2\\&\le&\frac{\epsilon}{2}+\frac{\epsilon}{2(1+\frac{\epsilon}{2})^2}\left(1+\frac{\epsilon}{2}\right)^2\;(\because(3))\\&=&\epsilon\end{eqnarray*}
\begin{equation}\therefore\;f'(a)=\cos a\end{equation}よってサインの微分はコサインなのです.
ε論法シリーズ

【2】無限積と級数の関係と収束性

【1】無限積の定義と収束・発散
絶対収束する二重級数・和の順序、コーシー積
正項の二重級数と和の順序
二重数列と二重級数(収束性と足し合わせの順)

実数論の練習問題

無限級数の収束性3(アーベル・ディリクレ)

シュトルツ・チェザロの定理(数列の極限)
【ε論法】極限の計算:limをεδに
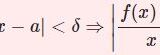
【ε論法】ε-δ論法によって微分する・例題7つ
【ε論法】カントール集合と悪魔の階段の連続性
【ε論法】トマエ関数は有理数の点では不連続

【ε論法】連続関数の和も積も合成も連続関数
【ε論法】一様コーシーな関数列と一様収束性
【ε論法】関数列が一様収束でないことの証明
【ε論法】関数列の各点収束と一様収束
【ε論法】一様連続でないことの証明
【ε論法】関数の一様連続性の証明
【ε論法】関数の連続性とδのテクニック
【ε論法】コーシー列でないことの証明
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。