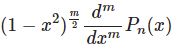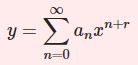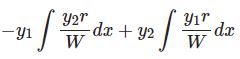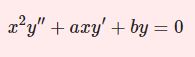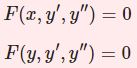前回学んだ級数法を用います。前回の記事はこちら
\begin{equation}(1-x^2)y^{\prime\prime}-2xy'+\nu(\nu+1)y=0\tag{1}\end{equation}の解法を示す.またルジャンドル多項式が解となる場合について詳しく解説する。
もくじ
級数法の練習として解いてみてください。
$$y=\sum_{n=0}^\infty a_nx^n$$とおけば 漸化式は\begin{eqnarray*}&& a_0=-a_2\\&& a_3=0 \\&& (n+1)a_{n+2}=(n-1)a_n\;,\;n\geq 2\end{eqnarray*}$a_0$ と $a_1$ は任意です。従って $a_1$ を除く奇数項は $0$ で偶数項は $a_{2k+2}=-\displaystyle\frac{a_0}{2k+1}$ となります。よって特殊解は\begin{eqnarray*}y_1&=&a_1x \\y_2&=&a_0(1-x^2-\frac{x^4}{3}-\frac{x^6}{5}\cdots)\\&=&a_0\left(1-\frac{1}{2}x\ln\frac{1+x}{1-x}\right)\end{eqnarray*}特殊解の片方は多項式、もう片方は無限級数となっています。一般解は$$y(x)=ax+b\left(1-\frac{1}{2}x\ln\frac{1+x}{1-x}\right)$$とあらわされます。
同様に漸化式を計算します。\begin{eqnarray*}&& 3a_0+a_2=0 \\&& 2a_1+3a_3=0 \\&&(n+2)(n+1)a_{n+2}+(n+3)(2-n)a_n=0\;,\;s\geq 2\end{eqnarray*}偶数項は $a_2=-3a_0$ で残りは $a_4=a_6=\cdots =0$ となるため $a_0=1$ とすれば特殊解 $1-3x^2$ を得ます。奇数項の特殊解は $a_1=1$ として$$x-\sum^\infty_{m=1}\frac{m(m+1)}{(2m+1)(2m-1)}x^{2m+1}$$となります。ここで$$\frac{m(m+1)}{(2m+1)(2m-1)}x^{2m+1}=\frac{1}{8}\left(\frac{3}{2m-1}+\frac{1}{2m+1}+2 \right)$$とできることを利用すれば、この特殊解は$$x-\frac{1}{8}\left[ \frac{1+3x^2}{2}\ln\frac{1+x}{1-x} - \frac{x(1-3x^2)}{1-x^2}\right]$$今回も特殊解の片方は多項式、もう片方は無限級数となっています。一般解は$$y(x)=a(1-3x^2)+b\left[ x-\frac{1}{8}\left\{ \frac{1+3x^2}{2}\ln\frac{1+x}{1-x} - \frac{x(1-3x^2)}{1-x^2}\right\}\right]$$
$\nu=0,-1$ の場合は$$(1-x^2)y''-2xy'=0$$なので $y'=z$ とおけば1階微分方程式$$(1-x^2)z'-2xz=0$$を得ます。変数分離して$$\frac{dz}{z}=\frac{2x}{1-x^2}dx$$$$\therefore \ln|z|=\ln\frac{c_1}{|1-x^2|}$$$c_1$ は正負の値をとるので絶対値は外して$$y'=z=\frac{c_1}{1-x^2}$$もう1度積分して$$y=c_1\int\frac{dx}{1-x^2}=c_1\left(\frac{1}{2}\ln\frac{1+x}{1-x}+c_2\right)$$$$\therefore\quad y=a+b\ln\frac{1+x}{1-x}$$
$(1-x^2)$で割ると $x=0$ で解析的だと分かります。よって級数法を用います。$$y=\sum_{n=0}^\infty a_nx^n$$とおけば\begin{eqnarray*}y'&=&\sum_{n=0}^\infty na_nx^{n-1}\\y^{\prime\prime}&=&\sum_{n=0}^\infty n(n-1)a_nx^{n-2}\end{eqnarray*}これらを方程式(1)に代入して各項の係数を比較します。\begin{eqnarray*} &&(1-x^2)y^{\prime\prime}-2xy'+\nu(\nu+1)y \\ &=&\sum_{n=0}^\infty[n(n-1)a_nx^{n-2}-n(n-1)a_nx^n-2na_nx^n+\nu(\nu+1)a_nx^n] \\&=& \sum_{n=0}^\infty[(n+2)(n+1)a_{n+2}-(\nu+n+1)(-\nu+n)a_n]x^n=0\end{eqnarray*}$$\therefore\quad a_{n+2}=\frac{(\nu+n+1)(-\nu+n)}{(n+2)(n+1)}a_n\quad (n \ge 0)$$
以上をまとめると$$\begin{cases}a_0\;,\;a_1\; : \;任意\\a_{n+2}=\displaystyle\frac{(\nu+n+1)(-\nu+n)}{(n+2)(n+1)}a_n\quad (n \ge 0)\end{cases}$$漸化式は1つ飛びになっており,偶奇に分けて考えることになります。
まずは偶数項 $a_{2m}$ を計算します。\begin{eqnarray*}a_{2m}&=& \frac{(\nu+2m-1)(-\nu+2m-2)}{2m(2m-1)}a_{2m-2}\\ &\vdots&\\ &=& \frac{(\nu+2m-1)(\nu+2m-3)\cdots(\nu+1)\times(-\nu)(-\nu+2)\cdots(-\nu+2m-2)}{2^m m!\times 2^m(m-\frac{1}{2})(m-\frac{3}{2})\cdots\frac{1}{2}}a_0\\ &=& \frac{\frac{\nu+1}{2}\frac{\nu+3}{2}\cdots\frac{\nu+2m-1}{2}\times(-\frac{\nu}{2})(-\frac{\nu}{2}+1)\cdots(-\frac{\nu}{2}+m-1)}{m!(\frac{1}{2})_m}a_0 \\ &=&\frac{(\frac{\nu+1}{2})_m(-\frac{\nu}{2})_m}{(\frac{1}{2})_m m!}a_0\quad(m\ge 0)\end{eqnarray*}ただし $(x)_n$ はポッホハマー記号で$$\begin{cases}(x)_n\equiv x(x+1)\cdots(x+n-1)\quad(n\ge 1)\\ (x)_0\equiv1\end{cases}$$と定義されます。
次に奇数項 $a_{2m+1}$ を計算します。
\begin{eqnarray*}a_{2m+1}&=& \frac{(\nu+2m)(-\nu+2m-1)}{(2m+1)2m}a_{2m-1}\\ &\vdots&\\ &=& \frac{(\nu+2m)(\nu+2m-2)\cdots(\nu+2)\times(-\nu+1)(-\nu+3)\cdots(-\nu+2m-1)}{2^m m!\times 2^m(m+\frac{1}{2})(m-\frac{1}{2})\cdots\frac{3}{2}}a_1\\ &=& \frac{(\frac{\nu}{2}+1)(\frac{\nu}{2}+2)\cdots(\frac{\nu}{2}+m)\times(\frac{1-\nu}{2})(\frac{3-\nu}{2})\cdots(\frac{2m-1-\nu}{2})}{m!(\frac{3}{2})_m}a_1 \\ &=& \frac{(\frac{\nu}{2}+1)_m(\frac{1-\nu}{2})_m}{(\frac{3}{2})_m m!}a_1\quad(m\ge 0)\end{eqnarray*}
以上により無限級数 $\sum a_nx^n$ は任意定数2つ $a_0,a_1$ を含むので以下の一般解が構成されます。
\begin{eqnarray*}y&=&\sum_{n=0}^\infty a_nx^n\\&=&a_0\sum_{m=0}^\infty\frac{(\frac{\nu+1}{2})_m(-\frac{\nu}{2})_m}{(\frac{1}{2})_m m!}x^{2m}+a_1\sum_{m=0}^\infty\frac{(\frac{\nu}{2}+1)_m(\frac{1-\nu}{2})_m}{(\frac{3}{2})_m m!}x^{2m+1}\\ &=& a_0\;{}_2F_1\left[ \begin{matrix}\frac{\nu+1}{2},-\frac{\nu}{2}\\\frac{1}{2}\end{matrix};x^2 \right]+a_1x\;{}_2F_1\left[\begin{matrix}\frac{\nu}{2}+1,\frac{1-\nu}{2}\\\frac{3}{2}\end{matrix};x^2 \right]\end{eqnarray*}ここで ${}_2F_1$ はガウスの超幾何関数です。
ルジャンドルの微分方程式は2階ですので独立な特殊解が$2$つあります。今の場合\begin{eqnarray*}A_\nu(x)&\equiv& {}_2F_1\left[ \begin{matrix}\frac{\nu+1}{2},-\frac{\nu}{2}\\\frac{1}{2}\end{matrix};x^2 \right] \\ B_\nu(x)&\equiv& x\;{}_2F_1\left[\begin{matrix}\frac{\nu}{2}+1,\frac{1-\nu}{2}\\\frac{3}{2}\end{matrix};x^2 \right] \end{eqnarray*}の2つです。よって微分方程式(1)の一般解は$$\therefore\quad y(x)=a_0A_\nu(x)+a_1B_\nu(x)$$
ということで微分方程式が一応解けたわけですが $\nu$ が整数のときには $A_\nu , B_\nu$ の片方が多項式になるという面白い性質がありますので以下で確認しましょう。 なお(1)を見れば $\nu=-1,-2,-3,-4\cdots$ はそれぞれ $\nu=0,1,2,3\cdots$ のときと同じ式になるので,$\nu$ は非負整数を考えれば十分です。
$\nu$ が偶数のとき
$\nu=2\nu'$ とすると\begin{equation}a_{2m}=\frac{(\nu'+\frac{1}{2})_m(-\nu')_m}{(\frac{1}{2})_mm!}a_0\tag{2}\end{equation}ここで $(-\nu')_m$ に着目します。$$ (-\nu')_m=(-\nu') (-\nu'+1)\cdots( -\nu'+m-1)$$もし $m$ が $\nu'+1$ に達するとこの項はゼロとなります。なので $a_{2m}$ は $a_0$ , $a_2$ ,…, $a_{2\nu'}$ までは非ゼロで,それ以降 $a_{2\nu'+2}$ , $a_{2\nu'+4}$ ,…はゼロとなります。
すなわち $\nu$ が偶数のとき $A_\nu(x)$ は $\nu$ 次の多項式となります。一方 $a_{2m+1}$ はいつまでもゼロの項があらわれず,やはり無限級数のままです。
$\nu$ が奇数のとき
$\nu=2\nu'+1$ とすると$$a_{2m+1}=\frac{(\nu'+\frac{3}{2})_m(-\nu')_m}{(\frac{3}{2})_mm!}a_1$$ここで $(-\nu')_m$ に着目します。$$ (-\nu')_m=(-\nu') (-\nu'+1)\cdots( -\nu'+m-1)$$もし $m$ が $\nu'+1$ に達するとこの項はゼロとなります。なので $a_{2m+1}$ は $a_1$ , $a_3$ ,…, $a_{2\nu'+1}$ までは非ゼロで,それ以降 $a_{2\nu'+3}$ , $a_{2\nu'+5}$ ,…はゼロとなります。
すなわち $\nu$ が奇数のとき $B_\nu(x)$ は $\nu$ 次の多項式となります。一方 $a_{2m}$ はいつまでもゼロの項があらわれず,やはり無限級数のままです。
以上を総合すると
$\nu$ が非負整数のとき,ルジャンドルの微分方程式(1)の特殊解として $\nu$ 次の多項式が現れる。
実際に多項式を書き下そうとすると $\nu$ が増えるごとにしんどくなります。しかしこの $\nu$ 次多項式の任意定数をある条件下で決めたものをルジャンドル多項式といい、物理学でも時折現れますので重要です。次節ではこの多項式に焦点をあててみます。
前節より、ルジャンドルの微分方程式では $\nu$ が非負整数のとき2つの特殊解のうち1つが $\nu$ 次の多項式、もう1つが無限級数となることが分かりました。ここであらわれる多項式(を適切に定数倍したもの)がルジャンドル多項式 $P_n(x)$ です。例えば $P_0(x)=1$, $P_1(x)=x$ , $P_2(x)=\frac{3x^2-1}{2}$ といった感じです。
微分方程式の解は定数倍の不定性があります。これを確定するためにルジャンドル多項式は $P_n(1)=1$ となるよう定数が定められます。
$\nu$ が偶数のとき
$\nu=2n$ とします。このとき偶数項のほうの特殊解 $A_{2n}(x)$ が多項式になるのでしたね。これを変形していきます。(2)より\begin{eqnarray*}A_{2n}(x)&=& \frac{1}{a_0}\sum_{m=0}^\infty a_{2m}x^{2m}\\&=& \sum_{m=0}^n \frac{(n+\frac{1}{2})_m(-n)_m}{(\frac{1}{2})_mm!}x^{2m}\\ &=& \left(-\frac{1}{4}\right)^n\frac{(2n)!!}{(2n-1)!!} \sum_{m=0}^n \frac{(-1)^{m+n}}{(n+m)!(n-m)!}\frac{(2n+2m)!}{(2m)!}x^{2m}\\&=& \left(-\frac{1}{4}\right)^n\frac{(2n)!!}{(2n-1)!!} \sum_{r=n}^{2n} \frac{(-1)^{r}}{r!(2n-r)!}\frac{(2r)!}{(2r-2n)!}x^{2r-2n}\\ &=& \left(-\frac{1}{4}\right)^n\frac{(2n)!!}{(2n-1)!!} \sum_{r=n}^{2n} \frac{(-1)^{r}}{r!(2n-r)!}\frac{d^{2n}}{dx^{2n}}x^{2r} \\&=& \left(-\frac{1}{4}\right)^n\frac{(2n)!!}{(2n-1)!!} \sum_{r=0}^{2n} \frac{(-1)^{r}}{r!(2n-r)!}\frac{d^{2n}}{dx^{2n}}x^{2r}\\&=& \left(-\frac{1}{4}\right)^n\frac{1}{((2n-1)!!)^2} \frac{d^{2n}}{dx^{2n}}\sum_{r=0}^{2n}\binom{2n}{r}(-1)^{2n-r}x^{2r}\\ &=& \left(-\frac{1}{4}\right)^n\frac{1}{((2n-1)!!)^2} \frac{d^{2n}}{dx^{2n}}(x^2-1)^{2n}\\&=& \left(-\frac{1}{4}\right)^n\frac{1}{((2n-1)!!)^2} \frac{d^{2n}}{dx^{2n}}[(x+1)^{2n}(x-1)^{2n}] \end{eqnarray*}
ここで次の公式を使います。
$$\frac{d^n}{dx^n}f(x)g(x)=\sum^n_{k=0} \binom{n}{k}f^{(k)}g^{(n-k)}$$
数学的帰納法による\begin{eqnarray*}\frac{d^{n+1}}{dx^{n+1}}f(x)g(x)&=&\frac{d}{dx}\sum^n_{k=0} \binom{n}{k}f^{(k)}g^{(n-k)} \\&=&\sum^n_{k=0}\binom{n}{k}f^{(k)}g^{(n+1-k)}+\sum^n_{k=0}\binom{n}{k}f^{(k+1)}g^{(n-k)} \\&=&\sum^n_{k=0}\binom{n}{k}f^{(k)}g^{(n+1-k)}+\sum^{n+1}_{k=1}\binom{n}{k-1}f^{(k)}g^{(n+1-k)} \\&=& fg^{(n+1)}+f^{(n+1)}g+\sum^n_{k=1}f^{(k)}g^{(n+1-k)}\left(\frac{n!}{k!(n-k)!}+\frac{n!}{(k-1)!(n-k+1)!} \right) \\&=&\sum^{n+1}_{k=0}\binom{n+1}{k}f^{(k)}g^{(n+1-k)}\end{eqnarray*}
これにより\begin{eqnarray*}A_{2n}(x)&=& \left(-\frac{1}{4}\right)^n\frac{1}{((2n-1)!!)^2} \frac{d^{2n}}{dx^{2n}}[(x+1)^{2n}(x-1)^{2n}] \\&=& \left(-\frac{1}{4}\right)^n\frac{1}{((2n-1)!!)^2} \sum^{2n}_{k=0} \binom{2n}{k}\frac{d^k}{dx^k}[(x-1)^{2n}]\cdot\frac{d^{2n-k}}{dx^{2n-k}}[(x+1)^{2n}]\\&=& \left(-\frac{1}{4}\right)^n\frac{1}{((2n-1)!!)^2} \sum^{2n}_{k=0} \binom{2n}{k}\frac{(2n)!}{(2n-k)!}(x-1)^{2n-k}\cdot\frac{(2n)!}{k!}(x+1)^{k}\\&=& \left(-\frac{1}{4}\right)^n\frac{(2n)!!}{(2n-1)!!} \sum^{2n}_{k=0} \binom{2n}{k}^2 (x-1)^{2n-k} (x+1)^{k}\end{eqnarray*}$x=1$ を代入すると $k=2n$ 以外では $(x-1)$ の項がゼロになるので$$ A_{2n}(1)= \frac{(2n)!!}{(2n-1)!!} (-1)^n$$
ここで特殊解である多項式は任意定数 $a_0$ を用いて $a_0A_{2n}(x)$ でした。$x=1$ を代入したときに値$1$をとるように $a_0$ を調整したものをルジャンドル多項式といい $$P_{2n}(x)= a_0A_{2n}(x)$$ とおくと$$ P_{2n}(1)= a_0A_{2n}(1)=a_0 \frac{(2n)!!}{(2n-1)!!} (-1)^n $$従って $$a_0=\frac{(2n-1)!!}{(2n)!!}(-1)^n$$ととれば $P_{2n}(1)=1$となります。
よって $$P_{2n}(x)=\frac{(2n-1)!!}{(2n)!!}(-1)^n {}_2F_1\left[ \begin{matrix}\frac{2n+1}{2},-n\\\frac{1}{2}\end{matrix};x^2 \right]$$ これを一所懸命に変形すると以下の結論を得ます。
$\nu=2n$ のときルジャンドル多項式は微分方程式(1)の特殊解であり$$P_{2n}(x)= \left( -\frac{1}{4} \right)^n\sum^n_{m=0}(-1)^m \frac{(2n+2m)!}{(n-m)!(n+m)!(2m)!}x^{2m} $$
多項式の形を明示的に表しているので、本記事ではこれを「明示式」と呼ぶことにします。
奇数のルジャンドル多項式 $P_{2n+1}$ についても以上と同様の議論になります。ここでは省略します。
$$P_n(x)=\frac{1}{2^nn!}\frac{d^n}{dx^n}[(x^2-1)^n]$$
ロドリグの公式を2項展開して変形していくと\begin{eqnarray*}P_{2n}(x) &=& \frac{1}{4^n(2n)!}\frac{d^{2n}}{dx^{2n}}\sum^{2n}_{r=0}\binom{2n}{r}(-1)^{2n-r}x^{2r}\\&=& \frac{1}{4^n}\sum^{2n}_{r=0}\frac{(-1)^r}{r!(2n-r)!}\frac{d^{2n}}{dx^{2n}}x^{2r} \\&=& \frac{1}{4^n}\sum^{2n}_{r=n}\frac{(-1)^r}{r!(2n-r)!}\frac{d^{2n}}{dx^{2n}}x^{2r} \\&=& \frac{1}{4^n}\sum^{2n}_{r=n}\frac{(-1)^r}{r!(2n-r)!}\cdot\frac{(2r)!}{(2r-2n)!}x^{2r-2n}\\&=& \frac{1}{4^n}\sum^{n}_{m=0}\frac{(-1)^{m+n}}{(m+n)!(n-m)!}\cdot\frac{(2m+2n)!}{(2m)!}x^{2m}\\&=& \left( -\frac{1}{4} \right)^n\sum^n_{m=0}(-1)^m \frac{(2n+2m)!}{(n-m)!(n+m)!(2m)!}x^{2m}\end{eqnarray*}と確かに明示式と一致しました。3つ目の等号は、$r\le n-1$ の項は $2n$ 回微分すると$0$になることを利用しました。
方程式(1)の特殊解には別の表現もあります。 $n$ が実数 $\nu$ のとき(ただし負整数でない)、2つの特殊解は\begin{eqnarray*}P_\nu(x)&=&{}_2F_1\left[\begin{matrix}-\nu,\nu+1\\1\end{matrix};\frac{1-x}{2}\right]\\Q_\nu(x)&=&B\left(\nu+1,\frac{1}{2}\right)\frac{1}{(2x)^{\nu+1}} {}_2F_1\left[\begin{matrix}\frac{\nu+1}{2},\frac{\nu}{2}+1\\\nu+\frac{3}{2}\end{matrix};\frac{1}{x^2}\right]\end{eqnarray*} と表されます。${}_2F_1$ はガウスの超幾何関数で $P_\nu(x)$ を第1種ルジャンドル関数、$Q_\nu(x)$ を第2種ルジャンドル関数とよびます。
$P_\nu(x)$ は一般に無限級数ですが $n$ が非負整数のときは数列は途中で打ち切られて多項式となります。試しに $\nu=2$ とすると\begin{eqnarray*}P_2(x)&=& {}_2F_1\left[\begin{matrix}-2,3\\1\end{matrix};\frac{1-x}{2}\right]\\&=&\sum_{n=0}^\infty\frac{(-2)_n(3)_n}{(n!)^2}\left(\frac{1-x}{2}\right)^2\\&=& 1+(3x-3)+\frac{3}{2}(1-x)^2\\&=&\frac{1}{2}(3x^2-1)\end{eqnarray*}これはルジャンドル多項式に一致します。
$P_\nu(x)$ は $x=1$ のまわりに、 $Q_\nu(x)$ は $x=\infty$ のまわりに展開しています。本記事では $x=0$ まわりにばかり展開していますが、本来フロベニウス法は、好きな確定特異点で用いてよいのです。特異点と解法の関係についてはフックス型微分方程式シリーズを順番にご覧ください。
次の記事:
ルジャンドル関数の導出はこちら:
ルジャンドル多項式の積分表示はこちら:
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。

【Amazon】常微分方程式 (技術者のための高等数学)
常微分方程式シリーズ
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。