Integrals and Miscellaneous 18

曲面の曲がり具合② ～主曲率とガウス曲率～

ガウスの公式とワインガルテンの公式

曲率に関する「驚異の定理」と可展面

曲面の面積とガウス写像の面積（ガウス曲率のもつ意味）

ダルブーフレームと測地的曲率・捩率・法曲率

From @SrinivasR1729:
If we have integrals:\begin{eqnarray*}\int_0^\infty\left(e^{\frac{2}{3}x}-\frac{2}{3}\right)^2\frac{\tanh\frac{x}{2}+\tanh2x}{x}e^{-4x}dx&=&\frac{2}{9}\ln P\\\int_0^\infty\left(e^{\frac{2}{3}x}+\frac{2}{3}\right)^2\frac{\tanh\frac{x}{2}+\tanh2x}{x}e^{-4x}dx&=&\frac{2}{9}\ln Q\end{eqnarray*}then show that $$\sqrt[12]{PQ}=\frac{\sqrt[3]{2}\G(\frac{1}{3})^9}{5^\frac{3}{2} 3^\frac{2}{3}\pi^\frac{9}{2}}$$PROOF.$$K(a,b):=\int_0^\infty e^{-ax}\tanh bx\frac{dx}{x}\quad(a,b>0)$$\begin{eqnarray*}\dd{K}{a} &=& -\int_0^\infty e^{-ax}(1-e^{-2bx})\sum_{n=0}^\infty(-1)^ne^{-2bnx}dx \\&=&-\sum_{n=0}^\infty(-1)^n\left(\frac{1}{a+2bn}-\frac{1}{a+2b+2bn}\right) \\&=& -\sum_{n=0}^\infty(-1)^n\left(\frac{1}{a+4bn}-\frac{2}{a+2b+4bn}+\frac{1}{a+4b+4bn}\right) \\&=&\frac{1}{4b}\left[\psi\left(\frac{a}{4b}\right)-2\psi\left(\frac{a+2b}{4b}\right)+\psi\left(\frac{a+4b}{4b}\right)\right]\end{eqnarray*}Therefore,$$K(a,b)=\ln\frac{\G(\frac{a}{4b})\G(\frac{a+4b}{4b})}{\G(\frac{a+2b}{4b})^2}+C(b)$$We find $K\to 0$ as $a\to \infty$ then$$K(a,b)=\ln\frac{\G(\frac{a}{4b})\G(\frac{a+4b}{4b})}{\G(\frac{a+2b}{4b})^2}$$Now we see that \begin{eqnarray*}&&\int_0^\infty\left(e^{\frac{2}{3}x}\mp\frac{2}{3}\right)^2\frac{\tanh\frac{x}{2}+\tanh2x}{x}e^{-4x}dx\\&=& K(8/3,1/2)+K(8/3,2)\mp\frac{4}{3}(K(10/3,1/2)+K(10/3,2))+\frac{4}{9}(K(4,1/2)+K(4,2))\end{eqnarray*}then we can find the closed forms of the integrals after boring calculation.

Adding the two integrals yields\begin{eqnarray*}\frac{2}{9}\ln PQ &=&2K(8/3,1/2)+2K(8/3,2)+\frac{8}{9}(K(4,1/2)+K(4,2)) \\ &=&\frac{2}{9}\ln\frac{2^4\G(\frac{1}{3})^{72}}{5^{18}3^8\pi^{54}}\end{eqnarray*}Hence,$$\sqrt[12]{PQ}=\frac{\sqrt[3]{2}\G(\frac{1}{3})^9}{5^\frac{3}{2} 3^\frac{2}{3}\pi^\frac{9}{2}}$$

$$\int_0^1\left(\frac{x^{p-1}}{1-x}-\frac{rx^{q-1}}{1-x^r}\right)dx=\psi\left(\frac{q}{r}\right)-\psi(p)+\ln r\;\quad(p,q,r>0)$$PROOF.\begin{eqnarray*}LHS &=& \lim_{\epsilon,\delta\to +0}\int_\epsilon^{1-\delta}\sum_{n=0}^\infty\left(x^{n+p-1}-rx^{rn+q-1}\right)dx \\&=& \lim_{\epsilon,\delta\to +0}\sum_{n=0}^\infty\left[\frac{(1-\delta)^{n+p}-\epsilon^{n+p}}{n+p}-\frac{(1-\delta)^{rn+q}-\epsilon^{rn+q}}{n+\frac{q}{r}}\right]\end{eqnarray*}By ratio test we find the $\epsilon$ terms converge and tend to zero. Hence,\begin{eqnarray*} &=& \lim_{\delta\to +0}\left[\frac{(1-\delta)^p}{p} F\left[\begin{matrix}1,p\\p+1\end{matrix};1-\delta\right]-\frac{r(1-\delta)^q}{q} F\left[\begin{matrix}1,\frac{q}{r}\\\frac{q}{r}+1\end{matrix};(1-\delta)^r\right]\right]\end{eqnarray*}Recall the formula proven here :$$F\left[\begin{matrix}a,b\\a+b\end{matrix};z\right]=\frac{1}{B(a,b)}\sum_{n=0}^\infty\frac{(a)_n(b)_n}{n!^2}(1-z)^n\left[2\psi(n+1)-\psi(a+n)-\psi(b+n)-\ln(1-z)\right]$$, which gives\begin{eqnarray*}&&\int_0^1\left(\frac{x^{p-1}}{1-x}-\frac{rx^{q-1}}{1-x^r}\right)dx \\&=& \lim_{\delta\to +0}\left[(1-\delta)^p\bigl(\psi(1)-\psi(p)-\ln\delta\bigr)-(1-\delta)^q\left\{\psi(1)-\psi\left(\frac{q}{r}\right)-\ln\bigl(1-(1-\delta)^r\bigr)\right\}\right] \\&=& \lim_{\delta\to +0}\left[\left\{\psi(1)-\psi(p)-\ln\delta+O(\delta)\right\}-\left\{\psi(1)-\psi\left(\frac{q}{r}\right)+O(\delta)\right\}+(1-\delta)^q\ln\bigl(1-(1-\delta)^r\bigr)\right]\\&=&\lim_{\delta\to +0}\left[-\psi(p)-\ln\delta+\psi\left(\frac{q}{r}\right)+O(\delta)+(1-\delta)^q\ln r\delta(1+O(\delta))\right]\\&=&\lim_{\delta\to +0}\left[-\psi(p)-\ln\delta+\psi\left(\frac{q}{r}\right)+(1-\delta)^q\ln r\delta +O(\delta)\right]\\&=&\psi\left(\frac{q}{r}\right)-\psi(p)+\ln r\end{eqnarray*}

REFERENCE:
G.E.Andrews, G.C.Berndt, "Ramanujan's Lost Notebook IV" (2013), §6.2

Ramanujan's Lost Notebook Part IV(rakuten,ebook)

Ramanujans Lost Notebook Part 4 [Paperback,Amazon]

Suppose $a,c>0$ , $b>1$ then$$I(a,b,c):=\int_0^1\left(\frac{x^{c-1}}{1-x}-\frac{bx^{bc-1}}{1-x^b}\right)\sum_{k=0}^\infty x^{ab^k}dx=\psi\left(\frac{a}{b}+c\right)+\ln\frac{b}{a}$$PROOF. We consider the partial sum, namely\begin{eqnarray*}I_n(a,b,c) &=& \int_0^1\left(\frac{x^{c-1}}{1-x}-\frac{bx^{bc-1}}{1-x^b}\right)\sum_{k=0}^n x^{ab^k}dx \\&=& \sum_{k=0}^n\int_0^1\left(\frac{x^{ab^k+c-1}}{1-x}-\frac{bx^{ab^k+bc-1}}{1-x^b}\right)dx\end{eqnarray*}Recall the formula$$\int_0^1\left(\frac{x^{p-1}}{1-x}-\frac{rx^{q-1}}{1-x^r}\right)dx=\psi\left(\frac{q}{r}\right)-\psi(p)+\ln r\;\quad(p,q,r>0)$$which we obtained "2023/5/10" above. Hence,\begin{eqnarray*}I_n(a,b,c)&=&\sum_{k=0}^n\left[\psi(ab^{k-1}+c)-\psi(ab^k+c)+\ln b\right] \\&=& \psi\left(\frac{a}{b}+c\right)-\psi(ab^n+c)+(n+1)\ln b\end{eqnarray*}We deduced here that$$\psi(x+1)=\frac{1}{2x}+\log x-\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)e^{-xt}dt$$From $|\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}|\le \frac{1}{2}$ it follows that $$\psi(x)\approx \ln x \quad\mathrm{as} \;x\to\infty$$So taking the limit of $n\to \infty$ yields\begin{eqnarray*}I(a,b,c)&=&\lim_{n\to\infty}\left[\psi\left(\frac{a}{b}+c\right)-\ln(ab^n+c)+(n+1)\ln b\right]\\&=&\psi\left(\frac{a}{b}+c\right)+\ln\frac{b}{a}\end{eqnarray*}

Especially when $a=b$ , $c=1$ , the result is$$I(a,a,1)=\int_0^1\frac{1-ax^{a-1}+(a-1)x^a}{(1-x)(1-x^a)}\sum_{k=1}^\infty x^{a^k}dx=1-\g\quad(a>1)$$Besides, setting $a=2,3$ the special values are\begin{eqnarray*}&&\int_0^1\frac{1}{1+x}\sum_{k=1}^\infty x^{2^k}dx=1-\g \\ &&\int_0^1\frac{1+2x}{1+x+x^2}\sum_{k=1}^\infty x^{3^k}dx=1-\g\end{eqnarray*}

REFERENCE:
【γ16】ビネの第1公式（導出が技巧的！）
G.E.Andrews, G.C.Berndt, "Ramanujan's Lost Notebook IV" (2013), §6.2

Ramanujan's Lost Notebook Part IV(rakuten,ebook)

Ramanujans Lost Notebook Part 4 [Paperback,Amazon]

From @SeriesIntegral $$I:=\int_0^\pi\ln\left(\frac{5}{4}+\cos x\right)dx=0$$PROOF.$$f(z):=\frac{\ln(z+\frac{1}{2})}{z}dz$$We define the contour $C$ as below.

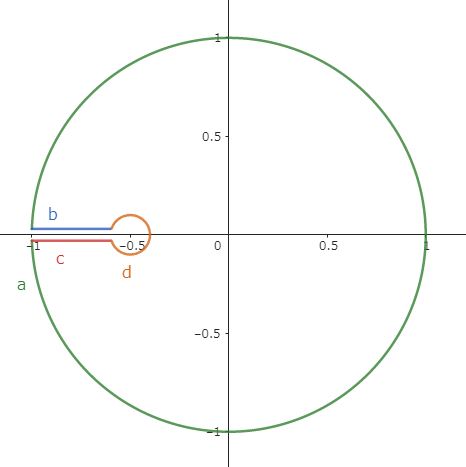
The residue theorem gives $$\oint_C f(z)dz=-2\pi i\ln 2$$and we calculate the four paths as:\begin{eqnarray*}\oint_C f(z)dz&=&i\int_0^\pi\ln\left(e^{i\t}+\frac{1}{2}\right)d\t +i\int_{-\pi}^0\ln\left(e^{i\t}+\frac{1}{2}\right)d\t\\&&+i\int_\pi^{-\pi}\frac{\epsilon e^{i\t}\ln(\epsilon e^{i\t})}{\epsilon e^{i\t}-\frac{1}{2}}d\t+\int_0^\frac{1}{2}\frac{\ln x-i\pi}{-x-\frac{1}{2}}(-dx)+\int^0_\frac{1}{2}\frac{\ln x+i\pi}{-x-\frac{1}{2}}(-dx)\\&=& i\int_0^\pi\ln\left(\frac{5}{4}+\cos \t\right)d\t-2\pi i\int_0^\frac{1}{2}\frac{dx}{x+1/2} \\&=& iI-2\pi i\ln2\end{eqnarray*}$$\therefore\quad I=0$$

From @SeriesIntegral $$\sum_{n=1}^\infty (-1)^n\ln\left(1+\frac{1}{n}\right)=\ln\frac{2}{\pi}$$PROOF.$$S_N:=\sum_{n=1}^N (-1)^n\ln\left(1+\frac{1}{n}\right)$$\begin{eqnarray*}S_{2N} &=& \sum_{n=1}^N\ln\frac{(2n+1)(2n-1)}{(2n)^2} \\&=& \ln\frac{\G(N+\frac{3}{2})\G(N+\frac{1}{2})}{\G(N+1)\G(N+1)}+\ln\frac{2}{\pi}\end{eqnarray*}Recall the formula$$\lim_{z\to\infty}\frac{\G(z+a_1)\G(z+a_2)\cdots\G(z+a_k)}{\G(z+b_1)\G(z+b_2)\cdots\G(z+b_k)}=1$$where $\sum_{i=0}^k a_i=\sum_{i=0}^k b_i$, proven here. Hence,$$\lim_{N\to\infty}S_{2N}=\ln\frac{2}{\pi}$$$$S_{2N+1}=S_{2N}-\ln\left(1+\frac{1}{2N+1}\right)\xrightarrow[]{N\to\infty} \ln\frac{2}{\pi}$$Therefore,$$\sum_{n=1}^\infty (-1)^n\ln\left(1+\frac{1}{n}\right)=\ln\frac{2}{\pi}$$

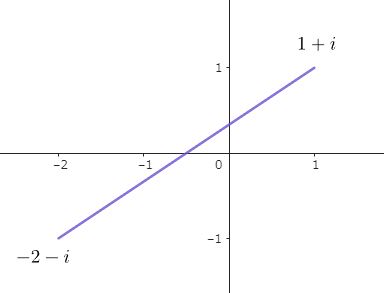
Find the image of the following line under the transformation $w=z^2$.

SOLUTION.
The line can be written as $z=(1-3t)+i(1-2t)$ where $0\le t\le 1$. We find$$w=u+iv=(5t^2-2t)+i\cdot(2t-1)(3t-1)$$Eliminating $t$ gives$$144u^2-120uv+25v^2-20u-48v-4=0$$which expresses a quadratic curve.
Now we consider the rotation $u+iv=(U+iV)e^{i\t}$ , $\tan\t=-\frac{5}{12}$. It follows that $$V=\frac{13}{4}U^2-\frac{1}{13}$$Hence, we conclude that the image of $w=z^2$ is the parabola created by rotating $v=\frac{13}{4}u^2-\frac{1}{13}$ by $\arctan(-\frac{5}{12})$ around the origin.

$$I(s):=\int_0^1\frac{\mathrm{artanh}sx}{x}dx=\frac{\Li_2(s)-\Li_2(-s)}{2}$$PROOF.\begin{eqnarray}I(s) &=& \sum_{n=0}^\infty\frac{s^{2n+1}}{2n+1}\int_0^1 x^{2n}dx \\&=& \sum_{n=0}^\infty\frac{s^{2n+1}}{(2n+1)^2} \\&=& \Li_2(s)-\frac{1}{4}\Li_2(s^2)\tag{1} \\ &=& \frac{\Li_2(s)-\Li_2(-s)}{2}\tag{2}\end{eqnarray}Especially,\begin{eqnarray}I(1)&=&\frac{\pi^2}{8} \\I(\phi^{-1}) &=& \frac{\pi^2}{12}-\frac{3}{4}\ln^2\phi \\ I(\phi^{-3}) &=& \frac{\pi^2}{24}-\frac{3}{4}\ln^2\phi\end{eqnarray}

REFERENCE:

多重対数関数（ポリログ）の関係式一覧・証明付き

John M. Campbell, Some nontrivial two-term dilogarithm identities, Irish Math. Soc. Bulletin Number 88 (2021)

From @AlnDkra $$I:=\int_0^1 x^x (1-x)^{1-x}\sin(\pi x)dx=\frac{\pi e}{24}$$PROOF.$$f(z):=z^z(1-z)^{1-z}e^{i\pi z}=e^{z\ln z+(1-z)\ln(1-z)+i\pi z}$$We also define the contour $C$ encircling the two branch points $0,1$ counter-clockwise, composed of two small arcs and two lines along the real axis. And we suppose$$-\pi\le\arg z<\pi\;,\; 0\le \arg(1-z)<2\pi$$ The branch cut exists just between $0$ and $1$, for we find f(z) is continuous when crossing the real axis at $-\epsilon$ and $1+\epsilon$.

\begin{eqnarray*}\oint_Cf(z)dz &=& \int_1^0 e^{x\ln x+(1-x)(\ln(1-x)+2\pi i)+i\pi x}dx+\int_0^1 e^{x\ln x+(1-x)\ln(1-x)+i\pi x}dx\\&=& 2i\int_0^1 x^x (1-x)^{1-x}\sin(\pi x)dx \\&=& 2iI\end{eqnarray*}Then we calculate the residue:\begin{eqnarray*}\oint_Cf(z)dz &=& -2\pi i\mathrm{Res}_{z=\infty}f(z) \\&=& 2\pi i\mathrm{Res}_{z=0}\frac{1}{z^2}f\left(\frac{1}{z}\right)\\&=& 2\pi i\mathrm{Res}_{z=0}\left[\frac{1}{z^2}e^{-\frac{1}{z}\ln(1-z)}-\frac{1}{z^3}e^{-\frac{1}{z}\ln(1-z)}\right]\end{eqnarray*}We obtained here that$$\mathrm{Res}_{z=0}\left[\frac{1}{z^2}e^{-\frac{1}{z}\ln(1-z)}\right]=\frac{e}{2}$$Expanding the remaining term:\begin{eqnarray*}\frac{1}{z^3}e^{-\frac{1}{z}\ln(1-z)} &=& \frac{1}{z^3}\sum_{n=0}^\infty\frac{(-1)^n\ln^n(1-z)}{n!z^n}\\&=&\frac{1}{z^3}\left[1-\frac{1}{z}\ln(1-z)+\frac{1}{2!z^2}\ln^2(1-z)-\frac{1}{3!z^3}\ln^3(1-z)+\cdots\right]\\&=& \frac{1}{z^3}\Biggl[1+\frac{1}{z}\left(z+\frac{z^2}{2}+\frac{z^3}{3}\cdots\right)\\&&+\frac{1}{2!z^2}\left(z+\frac{z^2}{2}+\frac{z^3}{3}\cdots\right)^2\\&&+\frac{1}{3!z^3}\left(z+\frac{z^2}{2}+\frac{z^3}{3}\cdots\right)^3+\cdots\Biggr]\end{eqnarray*}Focusing on $z^{-1}$ terms to get\begin{eqnarray*}\mathrm{Res}_{z=0}\left[\frac{1}{z^3}e^{-\frac{1}{z}\ln(1-z)}\right]&=&\frac{1}{3}+\frac{1}{2}\left(\frac{1}{4}+\frac{2}{3}\right)+\frac{1}{3!}\left(\frac{3}{4}+\frac{3}{3}\right)+\frac{1}{4!}\left(\frac{6}{4}+\frac{4}{3}\right)+\cdots \\&=& \frac{1}{3}\left(1+1+\frac{1}{2!}+\frac{1}{3!}+\cdots\right)+\frac{1}{4}\left(\frac{1}{2}+\frac{3}{3!}+\frac{6}{4!}+\cdots\right)\\&=&\frac{e}{3}+\frac{1}{4}\cdot\frac{1}{2}\left(1+\frac{1}{1!}+\frac{1}{2!}+\cdots\right)\\&=&\frac{e}{3}+\frac{e}{8}=\frac{11}{24}e\end{eqnarray*}$$\therefore\quad \oint_Cf(z)dz=2\pi i\left(\frac{e}{2}-\frac{11}{24}e\right)=2\pi i\frac{e}{24}$$Hence,$$I=\frac{\pi e}{24}$$

From @SeriesIntegral $$I:=\int_0^\infty\ln\frac{1+x^2+x^4+x^6}{1+x^6}dx=\pi(\sqrt{2}-1)$$PROOF.\begin{eqnarray*}I &=& \int_0^1\left(1+\frac{1}{x^2}\right)\ln\frac{1+x^2+x^4+x^6}{1+x^6}dx \\&=& \int_0^1\left(1+\frac{1}{x^2}\right)\ln\frac{1+x^4}{1-x^2+x^4}dx\\&=&\left[\left(x-\frac{1}{x}\right)\ln\frac{1+x^4}{1-x^2+x^4}\right]_0^1- \int_0^1\left(x-\frac{1}{x}\right)\left(\frac{4x^3}{1+x^4}-\frac{4x^3-2x}{1-x^2+x^4}\right)dx\\&=&4\int_0^1\frac{x^2-x^4}{1+x^4}dx+2\int_0^1\frac{2x^4-3x^2+1}{1-x^2+x^4}dx\\&=& 4\int_0^1\frac{1+x^2}{1+x^4}dx-2\int_0^1\frac{1+x^2}{1-x^2+x^4}dx \\&=& 2\sqrt{2}\Bigl[\arctan(\sqrt{2}x+1)+\arctan(\sqrt{2}x-1)\Bigr]_0^1-2\left[\arctan\frac{x}{x^2-1}\right]_0^1 \\&=& \pi(\sqrt{2}-1)\end{eqnarray*}

Ramanujan's Master Theoremの留数定理による導出

Frullani積分とRamanujanによる一般化

$$I:=\int_0^\infty x^{p-1}\left(\frac{2}{1+\sqrt{1+4x}}\right)^q dx\quad ,\;q>0\;,\;0<p<\frac{q}{2}$$SOLUTION.\begin{eqnarray*} I&=& \int_0^\infty y^{p-1}(1+y)^{p-q-1}(1+2y)dy\quad(x=y+y^2) \\&=& \int_0^1 z^{p-1}(1-z)^{q-2p-1}(1+z)dz\quad(y=\frac{z}{1-z}) \\&=& B(p,q-2p)+B(p+1,q-2p) \\&=& \frac{\G(p)\G(q-2p)}{\G(q-p)}+\frac{\G(p+1)\G(q-2p)}{\G(q-p+1)} \\&=&\frac{q\G(p)\G(q-2p)}{\G(q-p+1)}\end{eqnarray*}Hence,$$\int_0^\infty x^{p-1}\left(\frac{2}{1+\sqrt{1+4x}}\right)^q dx=\frac{q\G(p)\G(q-2p)}{\G(q-p+1)}$$

$$I:=\int_0^\infty \frac{x^{p-1}dx}{(x+\sqrt{1+x^2})^q}\quad ,\;q>0\;,\;0<p<q$$SOLUTION.\begin{eqnarray*}I &=&\frac{1}{2^{p+1}}\int_0^1y^{\frac{q-p}{2}-1}(1-y)^{p-1}(1+y)dy\quad(x+\sqrt{1+x^2}=1/\sqrt{y})\\&=&\frac{1}{2^{p+1}}\left[B\left(\frac{q-p}{2},p\right)+B\left(\frac{q-p}{2}+1,p\right)\right] \\&=&\frac{q\G(\frac{q-p}{2})\G(p)}{2^{p+1}\G(\frac{q+p}{2}+1)}\end{eqnarray*}Hence,$$\int_0^\infty \frac{x^{p-1}dx}{(x+\sqrt{1+x^2})^q}=\frac{q\G(\frac{q-p}{2})\G(p)}{2^{p+1}\G(\frac{q+p}{2}+1)}$$

From @SrinivasR1729:
$$I:=\int_V\frac{1+x^2+y^2+z^2+w^2}{\sqrt[3]{1-x^2-y^2-z^2-w^2}}dxdydzdw\;,\quad V=\left\{(x,y,z,w)|x^2+y^2+z^2+w^2\le 1\right\}$$SOLUTION.
Substituting$$\begin{cases}x&=&r\cos\t_3\\y&=&r\sin\t_3\cos\t_2\\ z&=& r\sin\t_3\sin\t_2\cos\t_1\\w&=& r\sin\t_3\sin\t_2\sin\t_1\end{cases}$$and we then find $$dxdydzdw=r^3\sin^2\t_3\sin\t_2\:drd\t_1d\t_2d\t_3$$\begin{eqnarray*}I &=& \int_0^1dr\int_0^{2\pi}d\t_1\int_0^\pi d\t_2\int_0^\pi d\t_3\frac{1+r^2}{\sqrt[3]{1-r^2}}r^3\sin^2\t_3\sin\t_2\\&=&2\pi^2\int_0^1\frac{1+r^2}{\sqrt[3]{1-r^2}}r^3dr\\&=&\pi^2\int_0^1\frac{u+u^2}{\sqrt[3]{1-u}}du\\&=& \pi^2\left[B\left(2,\frac{2}{3}\right)+B\left(3,\frac{2}{3}\right)\right]\\&=&\frac{63}{40}\pi^2\end{eqnarray*}