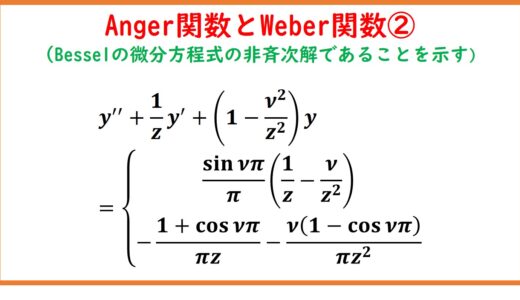
Previous posts:
$$\sum_{n=1}^\infty\frac{1}{n^2(2n+1)}=\frac{\pi^2}{6}+4\ln2-4$$PROOF.
\begin{eqnarray*}LHS&&=\sum_{n=1}^\infty\left(\frac{1}{n^2}-\frac{2}{n}+\frac{4}{2n+1}\right)\\&&=\frac{\pi^2}{6}+2\sum_{n=0}^\infty\left(\frac{1}{n+\frac{3}{2}}-\frac{1}{n+1}\right)\\&&=\frac{\pi^2}{6}-2\g-2\psi\left(\frac{3}{2}\right)\quad(*)\\&&=\frac{\pi^2}{6}-2\g-2\psi\left(\frac{1}{2}\right)-4\\&&=\frac{\pi^2}{6}+4\ln2-4\quad(*)\end{eqnarray*}(*) See
$$\sum_{n=1}^\infty\frac{1}{n^2(4n-1)}=-\frac{\pi^2}{6}-2\pi+12\ln2$$PROOF.
\begin{eqnarray*}LHS&&=\sum_{n=1}^\infty\left(-\frac{1}{n^2}-\frac{4}{n}+\frac{16}{4n-1}\right)\\&&=-\frac{\pi^2}{6}+4\sum_{n=0}^\infty\left(\frac{1}{n+\frac{3}{4}}-\frac{1}{n+1}\right)\\&&=-\frac{\pi^2}{6}+4\left(-\g-\psi\left(\frac{3}{4}\right)\right)\quad(*)\\&&=-\frac{\pi^2}{6}-2\pi+12\ln2\quad(*)\end{eqnarray*}(*) See
【γ9】ディガンマ関数の相反公式・倍数公式と特殊値・ゼータ関数(ガンマ関数の基礎シリーズ9)
$$\sum_{n=1}^\infty\frac{1}{n^2(3n-1)}=-\frac{\pi^2}{6}-\frac{\sqrt{3}}{2}\pi+\frac{9}{2}\ln3$$,which we can show in the same way as above.
$$\Li_3(1-e^{\frac{2}{3}\pi i})+\Li_3(1-e^{-\frac{2}{3}\pi i})=\frac{13}{9}\zeta(3)+\frac{\pi^2}{9}\ln3$$PROOF.
Recall the identity of $\Li_3(z)$$$\Li_3(z)+\Li_3(1-z)+\Li_3\left(1-\frac{1}{z}\right)=\zeta(3)+\frac{\pi^2}{6}\ln z-\frac{\ln^2z\ln(1-z)}{2}+\frac{\ln^3z}{6}$$,which we showed here:
Setting $z=e^{\frac{2}{3}\pi i}$,$$\Li_3(1-e^{\frac{2}{3}\pi i})+\Li_3(1-e^{-\frac{2}{3}\pi i})=-\Li_3(e^{\frac{2}{3}\pi i})+\zeta(3)+\frac{\pi^2}{9}\ln3+i\frac{2\pi^3}{81}$$We also obtained a special value:$$\Li_s(e^{\frac{2}{3}\pi i})=\left(\frac{1}{3^{s-1}}-1\right)\frac{\zeta(s)}{2}+i\frac{\zeta(s,\frac{1}{3})-\zeta(s,\frac{2}{3})}{2\cdot 3^{s-\frac{1}{2}}}$$in the upper link. Therefore,$$\Li_3(e^{\frac{2}{3}\pi i})=-\frac{4}{9}\zeta(3)+i\frac{2\pi^3}{81}$$Hence,$$\Li_3(1-e^{\frac{2}{3}\pi i})+\Li_3(1-e^{-\frac{2}{3}\pi i})=\frac{13}{9}\zeta(3)+\frac{\pi^2}{9}\ln3$$
$$\Li_2(1-e^{\frac{2}{3}\pi i})+\Li_2(1-e^{-\frac{2}{3}\pi i})=\frac{2\pi^2}{9}$$PROOF.
Recall the identity of $\Li_2(z)$$$\Li_2(1-z)+\Li_2\left(1-\frac{1}{z}\right)=-\frac{\ln^2z}{2}$$,which we showed here:
Setting $z=e^{\frac{2}{3}\pi i}$, we get the upper identity in red.
\begin{eqnarray*}\sum_{n=1}^\infty\frac{H_{2n}}{(2n+1)^2}&=&\frac{7}{16}\zeta(3)\\\sum_{n=1}^\infty\frac{H_{2n}}{n^2}&=&\frac{11}{4}\zeta(3)\\\sum_{n=1}^\infty\frac{H_{2n+1}}{n^2}&=&\frac{11}{4}\zeta(3)+\frac{\pi^2}{6}+4\ln2-4\\\sum_{n=1}^\infty\frac{H_{2n}}{(2n+1)^3}&=&\frac{17\pi^4}{1440}-\Li_4\left(\frac{1}{2}\right)-\frac{7}{8}\zeta(3)\ln2+\frac{\pi^2}{24}\ln^22-\frac{\ln^42}{24}\\\sum_{n=0}^\infty\frac{H_{2n+1}}{(2n+1)^3}&=&\frac{\pi^4}{45}-\Li_4\left(\frac{1}{2}\right)-\frac{7}{8}\zeta(3)\ln2+\frac{\pi^2}{24}\ln^22-\frac{\ln^42}{24}\\\sum_{n=1}^\infty\frac{H_{2n}}{n^3}&=&-\frac{\pi^4}{15}+8\Li_4\left(\frac{1}{2}\right)+7\zeta(3)\ln2-\frac{\pi^2}{3}\ln^22+\frac{\ln^42}{3}\\\sum_{n=1}^\infty\frac{H_{2n}^2}{n^2}&=&4\Li_4\left(\frac{1}{2}\right)+\frac{3\pi^4}{80}+\frac{7}{2}\zeta(3)\ln2-\frac{\pi^2}{6}\ln^22+\frac{\ln^42}{6}\\\sum_{n=1}^\infty\frac{H_{2n}^2}{(2n+1)^2}&=&\Li_4\left(\frac{1}{2}\right)+\frac{11\pi^4}{2880}+\frac{7}{8}\zeta(3)\ln2-\frac{\pi^2}{24}\ln^22+\frac{\ln^42}{24}\\\sum_{n=1}^\infty\frac{O_{2n}}{n^2}&=&7\zeta(3)-2\pi G\\\sum_{n=1}^\infty\frac{O_{2n-1}}{n^2}&=&7\zeta(3)-2\pi G+\frac{\pi^2}{6}+2\pi-12\ln2\end{eqnarray*}Proved here:
An example by @integralien_\begin{eqnarray*}\int\frac{x-1}{x+x^2\ln x}dx&=&\int\frac{-x^{-2}+x^{-1}}{x^{-1}+\ln x}dx\\&=&\int\frac{(x^{-1}+\ln x)'}{x^{-1}+\ln x}dx\end{eqnarray*}Hence,$$\int\frac{x-1}{x+x^2\ln x}dx=\ln\left(\frac{1}{x}+\ln x\right)+C$$
\begin{eqnarray*}\sum_{n=1}^\infty\frac{H_{3n}}{n^2}&=&5\zeta(3)-\frac{\pi}{6\sqrt{3}}\left[\zeta\left(2,\frac{1}{3}\right)-\zeta\left(2,\frac{2}{3}\right)\right]\\\sum_{n=1}^\infty\frac{H_{3n-1}}{n^2}&=&\frac{14}{3}\zeta(3)-\frac{\pi}{6\sqrt{3}}\left[\zeta\left(2,\frac{1}{3}\right)-\zeta\left(2,\frac{2}{3}\right)\right]\\\sum_{n=1}^\infty\frac{H_{3n-2}}{n^2}&=&\frac{14}{3}\zeta(3)-\frac{\pi}{6\sqrt{3}}\left[\zeta\left(2,\frac{1}{3}\right)-\zeta\left(2,\frac{2}{3}\right)\right]+\frac{\pi^2}{6}-\frac{9}{2}\ln3+\frac{\sqrt{3}}{2}\pi\end{eqnarray*}PROOF here:
\begin{eqnarray}\sum_{n=1}^\infty\frac{H_{4n}}{n^2}&=&\frac{67}{8}\zeta(3)-2\pi G\\\sum_{n=1}^\infty\frac{H_{4n}}{n^3} &=& 52\Li_4\left(\frac{1}{2}\right)-\frac{43}{80}\pi^4+\frac{91}{2}\zeta(3)\ln2-\frac{13}{6}\pi^2\ln^22+\frac{13}{6}\ln^42\\\sum_{n=1}^\infty\frac{H^2_{4n}}{n^2}&=&13\Li_4\left(\frac{1}{2}\right)+\frac{2\pi^4}{15}+\frac{91}{8}\zeta(3)\ln2-\frac{7}{24}\pi^2\ln^22\\&&+\frac{13}{24}\ln^42-4G^2+2\pi G\ln2+4\pi\mathfrak{I}\Li_3(1-i)\end{eqnarray}PROOF here:
$$I:=\int_0^1\frac{\arctan^2x}{x^2}dx$$Substituting $\arctan x=y$$$I=\int_0^\frac{\pi}{4}\frac{y^2dy}{\sin^2y}$$Integrating by parts twice gives\begin{eqnarray*}I&=&-\frac{\pi^2}{16}+\frac{\pi}{4}\ln2-2\int_0^\frac{\pi}{4}\ln(2\sin y)dy\\&=&-\frac{\pi^2}{16}+\frac{\pi}{4}\ln2+2\int_0^\frac{\pi}{4}\sum_{n=1}^\infty\frac{\cos2ny}{n}dy\\&=&-\frac{\pi^2}{16}+\frac{\pi}{4}\ln2+\sum_{n=1}^\infty\frac{1}{n^2}\sin\frac{n\pi}{2}\\ &=& -\frac{\pi^2}{16}+\frac{\pi}{4}\ln2+\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^2}\\ &=&-\frac{\pi^2}{16}+\frac{\pi}{4}\ln2+G\end{eqnarray*}where $G$ denotes Catalan's constant.
An example by @integralien_$$I:=\int e^x(x+1)^2\arctan xdx$$We can easily see$$\int e^x(x+1)^2dx=e^x(x^2+1)+C$$With the help of that, integrating $I$ by parts gives$$I=e^x(x^2+1)\arctan x-\int e^x(x^2+1)\frac{dx}{1+x^2}$$Hence,$$\int e^x(x+1)^2\arctan xdx=e^x(x^2+1)\arctan x-e^x+C$$
An example by @Harry_math_AdoO$$\int_0^1\frac{x\arcsin x}{\sqrt{(1-x^2)(2-x^2)}}dx=G$$PROOF.
Substituting $\arcsin x=y$\begin{eqnarray*}LHS&=&\int_0^\frac{\pi}{2}\frac{y\sin y}{\sqrt{1+\cos^2y}}dy\\&=&\int_0^\frac{\pi}{2}y\sin y\sum_{n=0}^\infty\frac{(-1)^n(2n-1)!!}{(2n)!!}\cos^{2n}ydy\\ &=& \sum_{n=0}^\infty\frac{(-1)^n(2n-1)!!}{(2n)!!}\int_0^\frac{\pi}{2}y\sin y\cos^{2n}ydy\\ &=& \sum_{n=0}^\infty\frac{(-1)^n(2n-1)!!}{(2n)!!}\left(-\frac{1}{2n+1}\left[y\cos^{2n+1}y\right]_0^\frac{\pi}{2}+\frac{1}{2n+1}\int_0^\frac{\pi}{2}\cos^{2n+1}ydy\right)\\&=&\sum_{n=0}^\infty\frac{(-1)^n(2n-1)!!}{(2n)!!(2n+1)}\int_0^\frac{\pi}{2}\cos^{2n+1}ydy\\ &=& \sum_{n=0}^\infty\frac{(-1)^n(2n-1)!!}{(2n)!!(2n+1)}\cdot\frac{(2n)!!}{(2n+1)!!}\\ &=&\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^2}\\ &=& G\end{eqnarray*}
We also find$$\int_0^\frac{\pi}{2}\frac{y\sin y}{\sqrt{1+\cos^2y}}dy=\int_0^\frac{\pi}{2}\ln\left(\cos y+\sqrt{1+\cos^2y}\right)dy$$by integration by parts. Hence,$$\int_0^\frac{\pi}{2}\mathrm{arcsinh}(\cos x)dx=G$$
$$\int_0^1\frac{\arctan^2(x^n)}{x^{n+1}}dx=\frac{1}{n}\left(G-\frac{\pi^2}{16}+\frac{\pi}{4}\ln2\right)$$PROOF.
Substituting $x^n=y$ gives \begin{eqnarray*}n\cdot LHS&=&\int_0^1\frac{\arctan^2y}{y^2}dy\\&=&\frac{1}{n}\int_0^\frac{\pi}{4}\frac{x^2}{\sin^2x}dx\\ &=& -\frac{\pi^2}{16}-\frac{\pi}{4}\ln2-2\int_0^\frac{\pi}{4}\ln(\sin x) dx\\ &=&-\frac{\pi^2}{16}+\frac{\pi}{4}\ln2-2\int_0^\frac{\pi}{4}\ln(2\sin x) dx\\ &=& -\frac{\pi^2}{16}+\frac{\pi}{4}\ln2+2\sum_{n=1}^\infty\frac{1}{n}\int_0^\frac{\pi}{4}\cos2nxdx\quad(*)\\ &=&-\frac{\pi^2}{16}+\frac{\pi}{4}\ln2+G \end{eqnarray*}(*) Fourier series of $\ln(2\sin x)$ . See:
$$I_n:=\int_{0}^{1}\arctan^n x dx$$\begin{eqnarray*}I_1&=&\frac{\pi}{4}-\frac{\ln 2}{2}\\I_2&=&\frac{\pi^2}{16}+\frac{\pi}{4}\ln 2-G\\I_3&=&\frac{63}{64}\zeta(3)-\frac{3}{4}\pi G+\frac{3}{32}\pi^2\ln2+\frac{\pi^3}{64}\\I_4&=&\frac{\pi^4}{256}+\frac{\pi^3}{32}\ln2-\frac{3}{8}\pi^2G+3\beta(4)-\frac{9}{64}\pi\zeta(3)\\I_5&=&\frac{\pi^5}{1024}+\frac{5\pi^4}{512}\ln2-\frac{5}{32}\pi^3G\\&&-\frac{45\pi^2}{512}\zeta(3)+\frac{15\pi}{4}\beta(4)-\frac{6975}{1024}\zeta(5)\end{eqnarray*}See here:
$$\int_0^\infty\frac{e^{-x^2}\cos(2x-4\arctan x)}{(1+x^2)^2}dx=\frac{2\sqrt{\pi}}{3e}$$We can show it with the help of Bourguet integral representation of the gamma function.See here:
By @integralsbot$$\int_{-\infty}^\infty\frac{dx}{(e^x+x+1)^2+\pi^2}=\frac{2}{3}$$PROOF.
Consider a contour integral$$\oint_C\frac{dz}{(e^z+z+1)^2+\pi^2}$$,where $C$ denotes the upper semicircle with large radius $R$. The denominator is $(e^z+z+1+i\pi)(e^z+z+1-i\pi)$, then we find that $z=\pi i$ is the only pole inside $C$, whose order is 2. Therefore,\begin{eqnarray*}\oint_C\frac{dz}{(e^z+z+1)^2+\pi^2}&=&2\pi i\displaystyle\lim_{z\to i\pi}\frac{d}{dz}\frac{(z-i\pi)^2}{(e^z+z+1)^2+\pi^2}\\&=&\frac{2}{3}\end{eqnarray*}
The remaining problem is to prove the big arc tends to zero as $R\to 0$.
By @integralsbot$$\int_0^\infty\frac{(1+x)^{b-c-2}}{\left(1+(1-s)x\right)^b}dx=\int_0^1\frac{(1-x)^c}{(1-sx)^b}dx$$PROOF.
The point is $(1+x)^{-c}$ will become $(1-y)^c$. So setting $y=\dfrac{x}{1+x}$ we get $$\int_0^\infty\frac{(1+x)^{b-c-2}}{\left(1+(1-s)x\right)^b}dx=\int_0^1\frac{(1-y)^{-b+c+2}}{\left(1+(1-s)\frac{y}{1-y}\right)^b}\frac{dy}{(1-y)^2}$$Hence,$$\int_0^\infty\frac{(1+x)^{b-c-2}}{\left(1+(1-s)x\right)^b}dx=\int_0^1\frac{(1-y)^c}{(1-sy)^b}dy$$
By @integralsbot$$\int_0^\infty\sin x\arctan\frac{1}{x}dx=\frac{\pi}{2}\left(1-\frac{1}{e}\right)$$PROOF.
Integration by parts gives$$LHS=\frac{\pi}{2}-\int_0^\infty\frac{\cos x}{1+x^2}dx$$Evaluating the second term by easy complex analysis, we get$$\int_0^\infty\sin x\arctan\frac{1}{x}dx=\frac{\pi}{2}\left(1-\frac{1}{e}\right)$$
By @infseriesbot$$\sum_{k=0}^n\frac{(a)_k}{k!}=\frac{(1+a)_n}{n!}$$PROOF.
It follows from mathematical induction that $$\sum_{k=0}^{n+1}\frac{(a)_k}{k!}=\frac{(1+a)_n}{n!}+\frac{(a)_{n+1}}{(n+1)!}=\frac{(1+a)_{n+1}}{(n+1)!}$$Hence,$$\sum_{k=0}^n\frac{(a)_k}{k!}=\frac{(1+a)_n}{n!}$$
\begin{eqnarray*}\int_0^\frac{\pi}{4}\arctan(\tan^{3+2\sqrt{2}} x)dx&=&\frac{\ln 2}{16}\ln(3+2\sqrt{2})\\\int_0^\frac{\pi}{4}\arctan(\tan^{11+2\sqrt{30}} x)dx&=&-\frac{\ln(1+\sqrt{2})\ln(4+\sqrt{15})}{8}-\frac{\ln(2+\sqrt{3})\ln(3+\sqrt{10})}{8}\\&&+\frac{3\ln(\frac{1+\sqrt{5}}{2})\ln(5+2\sqrt{6})}{8}+\frac{\ln2\ln(11+2\sqrt{30})}{16}\end{eqnarray*}
Substituting $\tan x \to x$ we get$$\int_0^1\frac{\arctan x^{3+2\sqrt{2}}}{1+x^2}dx$$
Then see H.Muzaffar,K.S. Williams, A restricted Epstein zeta function and the evaluation of some definite integrals , 2002 .
\begin{eqnarray}\int_0^\frac{\pi}{4}\arctan(\tan^2x)dx&=&\frac{\ln^2(\sqrt{2}-1)}{4}\\\int_0^\frac{\pi}{4}\arctan(\cot^2x)dx&=&\frac{\pi^2}{8}-\frac{\ln^2(\sqrt{2}-1)}{4}\end{eqnarray}See here:
$\chi_s(z)$ denotes the Legendre chi function.$$\int_0^\frac{\pi}{2}\arcsin(\mu\sin\t)d\t=\int_0^1\frac{\arcsin\mu x}{\sqrt{1-x^2}}dx=\chi_2(\mu)$$PROOF.
Let $\sin\t=x$ then the first equal appears immediately. Using the series expansion of $\arcsin z$, we get\begin{eqnarray*}\int_0^1\frac{\arcsin\mu x}{\sqrt{1-x^2}}dx&=&\sum_{n=0}^\infty\frac{(2n-1)!!\mu^{2n+1}}{(2n)!!(2n+1)}\int_0^1\frac{x^{2n+1}}{\sqrt{1-x^2}}dx\\ &=& \sum_{n=0}^\infty\frac{(2n-1)!!\mu^{2n+1}}{(2n)!!(2n+1)\cdot2}\int_0^1t^{n}(1-t)^{-\frac{1}{2}}dt\quad(x^2=t)\\ &=&\sum_{n=0}^\infty\frac{(2n-1)!!\mu^{2n+1}}{(2n)!!(2n+1)\cdot2}B\left(n+1,\frac{1}{2}\right) \\ &=& \sum_{n=0}^\infty\frac{(2n-1)!!\mu^{2n+1}}{(2n)!!(2n+1)\cdot2}\cdot\frac{n!2^{n+1}}{(2n+1)!!}\\ &=& \sum_{n=0}^\infty\frac{\mu^{2n+1}}{(2n+1)^2}\end{eqnarray*}The definition of $\chi_s(z)$ : $$\chi_s(z):=\sum_{n=0}^\infty\frac{z^{2n+1}}{(2n+1)^{s}}$$gives the equation above.
*A famous relation with $Li_s(z)$ is$$\chi_s(z)=\frac{1}{2}\left(\Li_s(z)-\Li_s(-z)\right)$$
$$\int_0^\infty\frac{dx}{\sqrt{x}\sqrt{x+1}\sqrt{2x+1}}=\frac{\G(\frac{1}{4})^2}{2\sqrt{2\pi}}$$PROOF.
Substituting $2x+1=y$ we get$$\int_0^\infty\frac{dx}{\sqrt{x}\sqrt{x+1}\sqrt{2x+1}}=\int_1^\infty\frac{dy}{\sqrt{y^2-1}\sqrt{y}}$$$t=\dfrac{1}{y}$ gives$$\int_1^\infty\frac{dy}{\sqrt{y^2-1}\sqrt{y}}=\int_0^1\frac{dt}{\sqrt{t}\sqrt{1-t^2}}$$Letting $t^2=u$, we get\begin{eqnarray*}\int_0^1\frac{dt}{\sqrt{t}\sqrt{1-t^2}}&=&\frac{1}{2}\int_0^1u^{-\frac{3}{4}}(1-u)^{-\frac{1}{2}}du\\&=&\frac{1}{2}B\left(\frac{1}{4},\frac{1}{2}\right)\\&=&\frac{1}{2}\frac{\sqrt{\pi}\G(\frac{1}{4})}{\G(\frac{3}{4})}\\&=&\frac{\G(\frac{1}{4})^2}{2\sqrt{2\pi}}\end{eqnarray*}
\begin{eqnarray}\int_0^\frac{\pi}{2}\t^2\sqrt{\cos \t} d\t&=&\frac{\pi\sqrt{2\pi}}{\G(\frac{1}{4})^2}\left(\pi^2+8G-16\right)\\\int_0^\frac{\pi}{2}\t^2\sqrt{\sec \t} d\t&=&\frac{\pi\sqrt{2\pi}}{4\G(\frac{3}{4})^2}\left(\pi^2-8G\right)\\\int_0^\pi\t^2\sqrt{\sin \t} d\t&=&\frac{\pi\sqrt{2\pi}}{\G(\frac{1}{4})^2}\left(3\pi^2+16G-32\right)\\\int_0^\pi\t^2\sqrt{\csc \t} d\t&=&\frac{\pi\sqrt{2\pi}}{4\G(\frac{3}{4})^2}\left(3\pi^2-16G\right)\\\int_0^\frac{\pi}{2}\t^2\sqrt{\cot\t} d\t &=&\frac{\pi\sqrt{2}}{8}\left(\frac{5}{12}\pi^2-\pi\ln2-\ln^2 2\right)\\\int_0^\frac{\pi}{2}\t^2\sqrt{\tan\t} d\t &=&\frac{\pi\sqrt{2}}{8}\left(\frac{5}{12}\pi^2+\pi\ln2-\ln^2 2\right)\end{eqnarray}
Proof is here:
Next post:
Integrals and Miscellaneous 10
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。