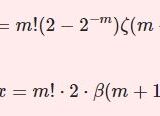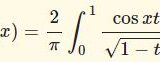極限計算を $\epsilon-\delta$ 論法で行う例題を考えましょう.
\begin{equation}\displaystyle\lim_{x\to0}e^{-\frac{1}{x^2}}\tag{1}\end{equation}を計算せよ.
$e^{-\infty}$ となるので答えは $0$ だろうと分かりますが,あえて $\epsilon-\delta$ でやります.ちなみに $f(x)=e^{-\frac{1}{x^2}}$ は下図のような形です.
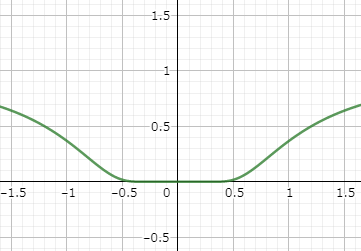
示したい式は $\lim$ を使って書かれています.収束先が $0$ であることを $\epsilon-\delta$ に書き直すと\begin{equation}\forall\epsilon>0\,,\,\exists\delta>0\,,\,|x|<\delta\Rightarrow|e^{-\frac{1}{x^2}}|<\epsilon\end{equation}$|x|$ を小さい数 $\delta$ で押さえる(0に近くする)と $|e^{-\frac{1}{x^2}}|$ も小さい数 $\epsilon$ で押さえられる(0に近くなる)よということです.
$\delta$ の取り方はいろいろあって中にはスマートなものもごり押しのものもあります。とにかく条件に合うような $\delta$ が探せればなんでもいいです。試しに $|x|<\delta$ として計算してみると$$\frac{1}{|x|}>\frac{1}{\delta}\Longrightarrow -\frac{1}{x^2}<-\frac{1}{\delta^2}$$となりますので\begin{eqnarray*}|e^{-\frac{1}{x^2}}|&=&e^{-\frac{1}{x^2}}\\&<&e^{-\frac{1}{\delta^2}}\le\epsilon\end{eqnarray*}つまり任意の $\epsilon$ に対して$$e^{-\frac{1}{\delta^2}}\le\epsilon$$となるように $\delta>0$ をとればいいのです。$\delta$ を,この条件を満たす $\epsilon$ の関数と考えたらよいのです。対数をとると$$-\frac{1}{\delta^2}\le\log\epsilon$$これを解いて$$\delta=\sqrt{-\frac{1}{\log\epsilon}}$$$\epsilon>0$ ですので、この式では $\epsilon\ge 1$ で機能しません。$\delta$ が虚数になってしまって $\delta>0$ を満たさないからです。そこで次のように $\delta$ を書き換えます。$$\delta=\begin{cases}\sqrt{-\displaystyle\frac{1}{\log\epsilon}}&\quad& (0<\epsilon<1)\\1&\quad&(\epsilon\ge 1)\end{cases}$$下の行で $\delta=1$ としていますが、これは適当に定数をとって実際に代入してみて、OKならそれでいいですし、だめならもっと小さい定数をとります。この $\delta$ を使って問題の式を導きましょう。
(1) $0<\forall\epsilon<1$ に対し、$$\delta=\sqrt{-\displaystyle\frac{1}{\log\epsilon}}>0$$ととると、$|x|<\delta$ ならば\begin{eqnarray*}|e^{-\frac{1}{x^2}}|&=&e^{-\frac{1}{x^2}}\\&<&e^{-\frac{1}{\delta^2}}\\&=&e^{\log\epsilon}=\epsilon\end{eqnarray*}$$\therefore\;|e^{-\frac{1}{x^2}}|<\epsilon$$
(2)次に $\epsilon\ge 1$ に対し、$\delta=1$ ととると、$|x|<\delta$ ならば$$|e^{-\frac{1}{x^2}}|<e^{-\frac{1}{\delta^2}}=\frac{1}{e}<1\le\epsilon$$$$\therefore\;|e^{-\frac{1}{x^2}}|<\epsilon$$
(1)(2)より、$\forall\epsilon>0$ に対し$$\delta=\begin{cases}\sqrt{-\displaystyle\frac{1}{\log\epsilon}}&\quad& (0<\epsilon<1)\\1&\quad&(\epsilon\ge 1)\end{cases}$$ととると、$$|x|<\delta\Longrightarrow |e^{-\frac{1}{x^2}}|<\epsilon$$
$$\therefore\quad\displaystyle\lim_{x\to0}e^{-\frac{1}{x^2}}=0$$
\begin{equation}\displaystyle\lim_{x\to0}\frac{\sqrt{7x+2}-\sqrt{x+2}}{x}\tag{2}\end{equation}
高校数学の知識で値は計算できます.\begin{eqnarray*}\displaystyle\lim_{x\to0}\frac{\sqrt{7x+2}-\sqrt{x+2}}{x}&=&\displaystyle\lim_{x\to0}\frac{(7x+2)-(x+2)}{x(\sqrt{7x+2}+\sqrt{x+2})}\\&=&\displaystyle\lim_{x\to0}\frac{6}{\sqrt{7x+2}+\sqrt{x+2}}\\&=&\frac{3}{\sqrt{2}}\end{eqnarray*}よって $\epsilon-\delta$ での表現は$$\forall\epsilon>0\,,\,\exists\delta>0\,,\,|x|<\delta\Rightarrow\left|\frac{\sqrt{7x+2}-\sqrt{x+2}}{x}-\frac{3}{\sqrt{2}}\right|<\epsilon$$となります.これを示しましょう.
$\epsilon>0$ に対して$$\d=\min\left[\frac{\epsilon}{9},\frac{1}{7}\right]$$ととります.$|x|<\d$ ならば $-\frac{1}{7}<x<\frac{1}{7}$ となるので$$\sqrt{7x+2}>1\;,\;\sqrt{x+2}>1$$が成立します.これを踏まえて以下の式変形を行います.\begin{eqnarray*}&&\left|\frac{\sqrt{7x+2}-\sqrt{x+2}}{x}-\frac{3}{\sqrt{2}}\right|\\&=&\left|\frac{6}{\sqrt{7x+2}+\sqrt{x+2}}-\frac{3}{\sqrt{2}}\right|\\&=&\frac{3}{\sqrt{2}}\frac{\left|\sqrt{7x+2}+\sqrt{x+2}-2\sqrt{2}\right|}{\sqrt{7x+2}+\sqrt{x+2}}\\&=&\frac{3}{\sqrt{2}}\frac{1}{\sqrt{7x+2}+\sqrt{x+2}}\left|(\sqrt{7x+2}-\sqrt{2})+(\sqrt{x+2}-\sqrt{2})\right|\\&<&\frac{3}{2\sqrt{2}}\left|(\sqrt{7x+2}-\sqrt{2})+(\sqrt{x+2}-\sqrt{2})\right|\\&\le& \frac{3}{2\sqrt{2}}\left(\left|\sqrt{7x+2}-\sqrt{2}\right|+\left|\sqrt{x+2}-\sqrt{2}\right|\right)\\&=&\frac{3}{2\sqrt{2}}\left(\frac{7}{\sqrt{7x+2}+\sqrt{2}}+\frac{1}{\sqrt{x+2}+\sqrt{2}}\right)|x|\\&<&\frac{3}{2\sqrt{2}}\left(\frac{7}{1+\sqrt{2}}+\frac{1}{1+\sqrt{2}}\right)|x|\\&=&\frac{6\sqrt{2}}{1+\sqrt{2}}|x|<6\sqrt{2}|x|\\&<&9|x|<9\d \le\epsilon\end{eqnarray*}でOKです.
ε論法シリーズ

【2】無限積と級数の関係と収束性

【1】無限積の定義と収束・発散
絶対収束する二重級数・和の順序、コーシー積
正項の二重級数と和の順序
二重数列と二重級数(収束性と足し合わせの順)

実数論の練習問題

無限級数の収束性3(アーベル・ディリクレ)

シュトルツ・チェザロの定理(数列の極限)
【ε論法】極限の計算:limをεδに
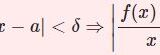
【ε論法】ε-δ論法によって微分する・例題7つ
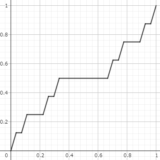
【ε論法】カントール集合と悪魔の階段の連続性
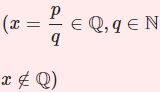
【ε論法】トマエ関数は有理数の点では不連続

【ε論法】連続関数の和も積も合成も連続関数
【ε論法】一様コーシーな関数列と一様収束性
【ε論法】関数列が一様収束でないことの証明
【ε論法】関数列の各点収束と一様収束
【ε論法】一様連続でないことの証明
【ε論法】関数の一様連続性の証明
【ε論法】関数の連続性とδのテクニック
【ε論法】コーシー列でないことの証明
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。