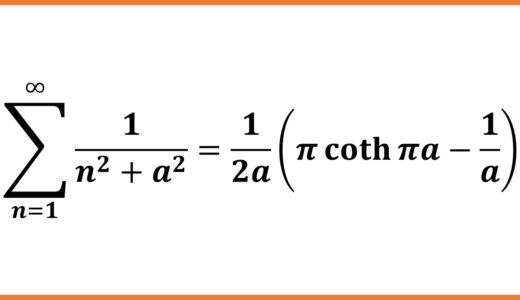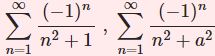独立させました。
【4】条件収束する無限積の収束性(Cauchy's test)
【5】条件収束する無限積の収束性2(積の順序・Pringsheim's Test・regularly convergent)
【7】関数列の無限積における具体例(ヴィエトの公式・ゼータ関数)
【8】整関数とワイエルシュトラスの因数分解定理①(基本乗積・種数)
【17】オイラーの五角数定理とワトソンの五重積(ヤコビ三重積から得られる公式たち)
「特殊関数」「微分方程式」カテゴリにも超幾何級数の記事があります。
Clausenの公式(一般化超幾何級数3F2を2F1に変える強力な式)
Well-poisedな一般化超幾何関数の変換公式とDougallの5F4-和公式
Whippleの7F6変換公式とDougallの7F6-和公式・6F5・5F4・4F3への応用(一般化超幾何関数)
4F3の特殊値の計算例(一般化超幾何級数のEuler積分表示)