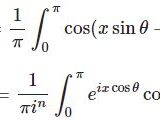「特殊関数」の記事一覧
調和数を含んだ級数とゼータ関数 part2
4次の多重対数関数を応用する積分
調和数を含んだ級数とゼータ関数 part1
多重対数関数（ポリログ）の関係式一覧・証明付き
arctan(μsin x)とarctan(μcsc x)の積分（二重対数関数と黄金比）
調和数を含んだ級数とζ(4) part2
Integrals and Miscellaneous 6
調和数を含んだ級数とζ(4) part1
x^m/(sin x)^nの積分（logsinのフーリエ展開・ディリクレのベータ関数）
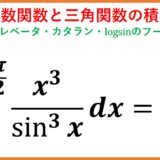
x^3/(sinx)^3の積分（ディリクレベータ関数・カタラン定数）
コサインの実数乗(cosθ)^μをフーリエ級数展開（ベータ関数の逆数の積分表示を応用）
ベータ関数の逆数の積分表示（複素積分演習）
ガンマ関数の逆数のテイラー展開（微分の繰り返し・係数の積分表示）
二重対数関数(dilogarithm)の等式(lntanhの積分と相反公式)
重積分を用いたバーゼル問題の解法②（ゼータ関数・座標変換）
重積分を用いたバーゼル問題の解法（ゼータ関数・座標軸の回転）
指数関数を含む積分演習 ： 3F2(1)型の超幾何級数とトマエの関係式
【ζ9】実部が正でのフルヴィッツゼータ関数の不等式・無限遠でのふるまい(ゼータ関数の基礎9)
【ζ8】ゼータ関数・全平面におけるRiemannの積分表示(複素積分・クシー関数)(ゼータ関数の基礎8)
【ζ7】ゼータ関数と素数・オイラー積・絶対収束(ゼータ関数の基礎7)
【ζ6】フルヴィッツゼータ関数のHermiteの公式(積分表示・Abel-Planaの和公式・ビネの公式)(ゼータ関数の基礎6)
【ζ5】リーマンゼータ関数の特殊値・関数等式とクシー関数・零点・全平面への接続（ゼータ関数の基礎5）
【ζ4】フルヴィッツゼータ関数のフーリエ展開・複素積分・Critical Stripへの拡張(ゼータ関数の基礎4)
【ζ3】ハンケル路によるフルヴィッツゼータ関数の値を求める・ベルヌーイ多項式・留数定理(ゼータ関数の基礎3)
【ζ2】フルヴィッツゼータ関数のハンケル路による積分表示・解析接続・留数計算(ゼータ関数の基礎2)
【ζ1】フルヴィッツゼータ関数の積分表示（ゼータ関数の基礎1）
ベータ関数のポッホハマー積分路を用いた積分表示（ガンマ関数論・複素積分）
「ビネの関数」の第2階乗型級数展開（スターリング近似の剰余項・ガンマ関数論）
「ビネの関数」の第1展開とビネの第1公式（ガンマ関数）
【γ20】ガンマ関数の漸近展開（ビネの第2公式・arctanの展開・スターリング級数）（ガンマ関数の基礎20）
【γ19】対数ガンマ関数におけるビネの第2公式の導出（アベル・プラナの和公式,ポリガンマ関数）（ガンマ関数の基礎19）
【γ18】対数ガンマ関数のフーリエ級数表示（ガンマ関数の基礎18）
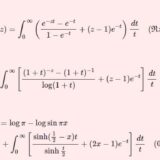
【γ17】ガンマ関数のクンマーによる積分表示
【γ16】ビネの第1公式（導出が技巧的！）
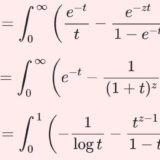
【γ15】ディガンマ関数の積分表示３選
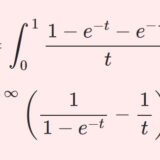
【γ14】オイラー定数の積分表示２選・調和数・積分評価（ガンマ関数の基礎14）
【γ13】ガンマ関数の放物線経路によるブルゲの積分表示・ハンケル路（ガンマ関数の基礎13）
【γ12】ガンマ関数の逆数・見た目だけは簡単な積分表示
Binetの第1公式の初等的証明（ログガンマの積分表示）後半
Binetの第1公式の初等的証明（ログガンマの積分表示）前半
【γ11】ガンマ関数の積分表示導出①（ハンケルとか）
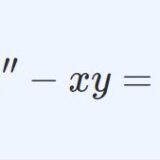
三角井戸型ポテンシャルとエアリー関数
【γ10】ポリガンマ関数の値、極、級数表示、ゼータ関数との関係（ガンマ関数の基礎シリーズ10）
【γ9】ディガンマ関数の相反公式・倍数公式と特殊値・ゼータ関数（ガンマ関数の基礎シリーズ9）
【γ8】ディガンマ関数の特殊値と極
【γ7】Γ(1/3),Γ(1/4),Γ(1/6)の値
【γ6】ログガンマの微分と4つの級数表示
【γ5】ガンマの微分とディガンマ関数
【γ4】ガンマ関数の倍数公式とガウスの乗法公式
【γ3】ベータ関数の定義・ガンマ関数との関係・三角関数での積分表示
【γ2】ガンマ関数の３つの乗積表示と相反公式（ガウス・オイラー・ワイエルシュトラス）
【γ1】ガンマ関数の定義・特殊値・解析接続・留数（ガンマ関数の基礎1）
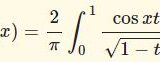
ラプラス変換でベッセル関数の積分表示を作る
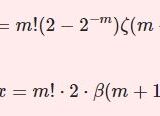
$\int\frac{x^m}{\sinh x}dx,\int\frac{x^m}{\cosh x}dx$ ゼータとベータ
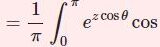
第1種変形ベッセル関数の積分表示
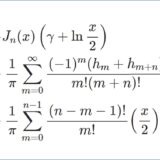
第2種ベッセル関数 $Y_\nu(x)$ の計算
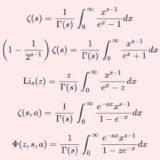
3種類のゼータ関数・多重対数関数とガンマ関数の関係
ゼータ関数値の求め方３選（フーリエ級数・パーセヴァルの等式・sin無限乗積）
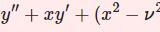
【D18】ベッセルの微分方程式と級数解
ルジャンドル多項式とシュレーフリの積分表示（ローラン展開・ロドリグの公式より）
ルジャンドル多項式とラプラスの積分表示（母関数とワイエルシュトラス置換）
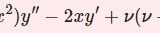
偶奇統一！第1種ルジャンドル関数
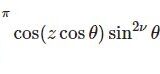
第1種ベッセル関数の積分表示(2) ポアソンの公式の導出
