「特殊関数」の記事一覧
ペー関数を使って楕円積分を変換する具体例
ヤコビの楕円関数６～12種類のフーリエ展開
ヤコビの楕円関数５～無限積表示と対数のフーリエ展開
ヤコビの楕円関数４～周期を変換する・ペー関数との関係
テータ関数11～ヤコビの楕円関数の登場
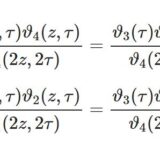
テータ関数10～ランデン変換と微分方程式
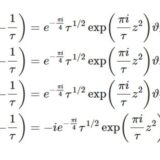
テータ関数９～ヤコビの虚数変換式
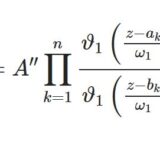
テータ関数８～ワイエルシュトラスのシグマ・ゼータ関数や楕円関数との関係
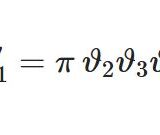
テータ関数７～無限積の導関数とテータ定数
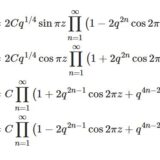
テータ関数６～無限積による表示
テータ関数５～ヤコビの基本関係式②
テータ関数４～ヤコビの基本関係式①
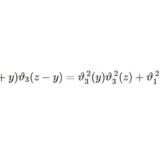
テータ関数３～周期性と極に注目した加法定理の導出
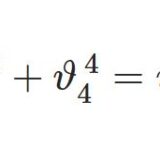
テータ関数２～零点・2乗の関係
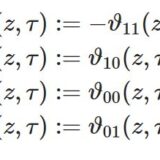
テータ関数１～定義と性質
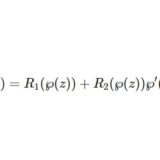
ワイエルシュトラスのペー関数８～任意の楕円関数をワイエルシュトラスの関数であらわす
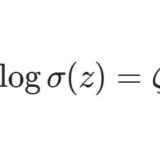
ワイエルシュトラスのペー関数７～シグマ関数：擬周期性をもつ整関数
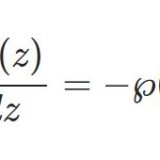
ワイエルシュトラスのペー関数６～擬周期性をもつゼータ関数
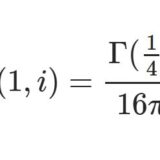
ワイエルシュトラスのペー関数５~周期・不変量・アイゼンシュタイン級数の計算
ワイエルシュトラスのペー関数４～三次方程式との関係・半周期
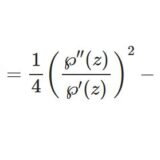
ワイエルシュトラスのペー関数３～同次性・加法定理等
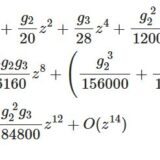
ワイエルシュトラスのペー関数２～係数の漸化式,積分公式
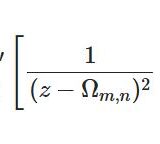
ワイエルシュトラスのペー関数１～基本的性質と級数展開
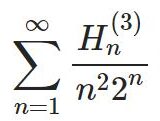
調和数を含んだ級数(Euler-sum)とゼータ関数 part17
logを含む難しい積分16
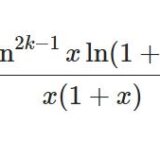
logを含む難しい積分15
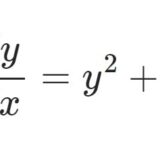
１階非線型微分方程式の例
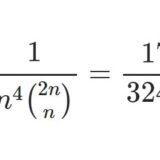
二項係数の逆数を含む級数
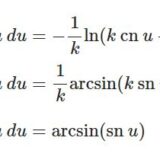
ヤコビの楕円関数を含む積分
ヤコビの楕円関数３（二重周期性・零点・極）
ある4F3の特殊値と逆三角関数および対数正弦積分
ヤコビの楕円関数２（定義域の拡張・半角公式・倍角公式・展開）
ヤコビの楕円関数（定義・導関数・加法定理）
楕円積分がみたす微分方程式とルジャンドルの関係式・singular value
完全楕円積分と算術幾何平均・上昇/下降変換
楕円積分の導入とその計算方法２(ルジャンドル・ヤコビの標準形)
楕円積分の導入とその計算方法１
【13】素数が無限積と級数をつなぐ（完全乗法的関数）
【12】無限積とガンマ関数
ハイパー階乗・K関数とGlaisher-Kinkelin定数②
ハイパー階乗・K関数とGlaisher-Kinkelin定数①
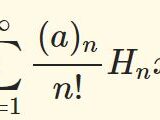
調和数と超幾何級数3
Integrals and Miscellaneous 18
logを含む難しい積分12(超幾何関数の微分の応用)
調和数を含んだ級数(Euler-sum)とゼータ関数 part16
logを含む難しい積分11(調和数とEuler sumの利用)
超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値３
超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値２
超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値１
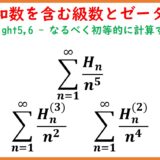
調和数を含んだ級数(Euler-sum)とゼータ関数 part14
Integrals and Miscellaneous 16
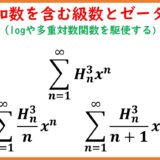
調和数を含んだ級数(Euler-sum)とゼータ関数 part13
logを含む難しい積分９
Whippleの7F6変換公式とDougallの7F6-和公式・6F5・5F4・4F3への応用（一般化超幾何関数）
Well-poisedな一般化超幾何関数の変換公式とDougallの5F4-和公式
Whippleの和定理（一般化超幾何級数3F2）
Watsonの定理（一般化超幾何級数3F2）
Dixonの定理の導出（一般化超幾何級数3F2）
Dixonの定理の導出2・オリジナル論文より（未完）
Integrals and Miscellaneous 15
ポリログを含む積分2（重積分・級数展開）
ポリログを含む積分1（重積分・級数展開）
Clausenの公式（一般化超幾何級数3F2を2F1に変える強力な式）
z=1/4における超幾何関数2F1の特殊値（代数的手法）
リーマンP方程式から超幾何関数の二次変換を導出
Integrals and Miscellaneous 14
複２次式の平方根を含む積分（楕円積分の応用）
超幾何関数2F1の特殊値と楕円積分2
超幾何関数2F1の特殊値と楕円積分1
超幾何関数のある変換公式の証明
z=1/9における超幾何関数2F1の特殊値６選（後編）
z=1/9における超幾何関数2F1の特殊値６選（前編）
超幾何関数に関するガウスの隣接関係式
双曲線関数を含む難しい積分１
二重のlogを含む積分１(ゼータ関数の微分)
超幾何関数2F1の変換公式１（基本の10個）
調和数を含んだ級数(Euler-sum)とゼータ関数 part12
調和数と超幾何級数2
調和数と超幾何級数1
logを含む難しい積分７（arcsinhの利用）
logを含む難しい積分６（4F3・楕円積分・二重対数関数）
logを含む難しい積分３（超幾何級数）
Integrals and Miscellaneous 10
log(sinh x)の対数正弦積分（調和数・ポリログ）
log(sin x)の2乗の対数正弦積分（調和数・ポリログ）
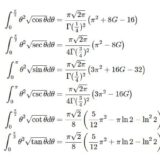
三角関数の平方根とx^2の積の積分
調和数を含んだ級数(Euler-sum)とゼータ関数 part11
arctan(x)のn乗の積分(フーリエ展開とディリクレベータ関数)
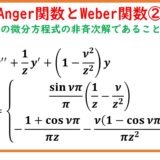
Anger関数とWeber関数②(ベッセル微分方程式の非斉次解)
Anger関数とWeber関数①(sinやcosの中にsinがある積分)
調和数を含んだ級数(Euler-sum)とゼータ関数 part10
調和数を含んだ級数(Euler-sum)とゼータ関数 part9
調和数を含んだ級数(Euler-sum)とゼータ関数 part8
調和数を含んだ級数(Euler-sum)とゼータ関数 part7
調和数を含んだ級数(Euler-sum)とゼータ関数 part6
調和数を含んだ級数(Euler-sum)とゼータ関数 part5
調和数を含んだ級数(Euler-sum)とゼータ関数 part4
調和数を含んだ級数とゼータ関数 part3
