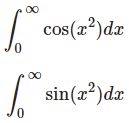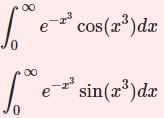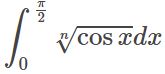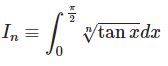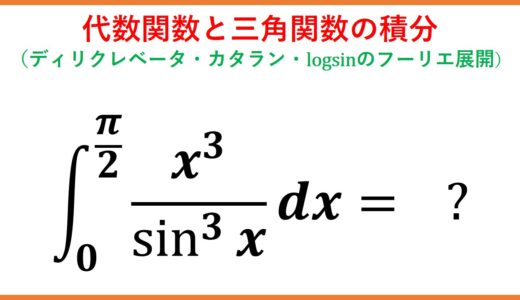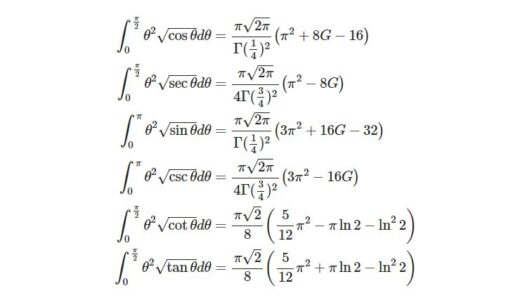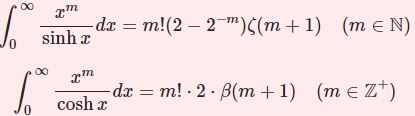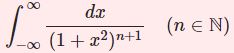微分方程式や特殊関数に関わるものはそちらのカテゴリに入っています。
ベータ関数などと絡めたものです。
ポリログや調和数と絡めたものは：
英語版：
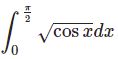Definite integral of √cos x , √sin x (with Gamma function)-integration sqrt(cos x),sqrt(sin x)
楕円積分の導入とその計算方法２(ルジャンドル・ヤコビの標準形)
楕円積分がみたす微分方程式とルジャンドルの関係式・singular value
logを含む難しい積分13（Euler-sumの応用,weight5）
複素積分演習 cosx と e^-xの混合（4分円の周回積分）
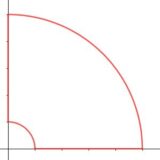Excercise of Contour Integral (Combination of Real and Imaginary Axis)
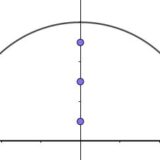複素積分演習（cos(log x)/(1+x^2)）
Ramanujan's Master Theoremの留数定理による導出
単発の細かい積分をストックしたページ：
Integrals and Miscellaneous 10
Integrals and Miscellaneous 11
Integrals and Miscellaneous 12
Integrals and Miscellaneous 13
Integrals and Miscellaneous 14
Integrals and Miscellaneous 15
Integrals and Miscellaneous 16
Integrals and Miscellaneous 17
Integrals and Miscellaneous 18
Integrals and Miscellaneous 19
Integrals and Miscellaneous 20
- logを含む難しい積分18（多重対数関数の積分ふくむ）前回はこちら： weight5の積分やEuler-sumを扱います。 はじめに$$\int_0^1\frac{\ln^3(1-x)\ln(1+x)}{x}dx$$を計算します。\begin{equat ...
- logを含む難しい積分17結果にゼータ関数が現れるタイプの積分を紹介。Euler-sumとよばれるタイプの無限級数とも関連する。
- logを含む難しい積分16前回の続きです。前回はこちら。 前回の(15)式で\begin{equation}\int_0^\infty\frac{\ln^{2k-1}x\ln(1+x)}{x(1+x)}dx=2\cdot(2k ...
- logを含む難しい積分15前回は： 今回から、何回かに分けて、互いにつながりのあるいくつかの積分を計算していきます。過去記事とダブるものがあるかもしれませんが、掘り起こすのも面倒なので、一からやっていきます。 もとはといえば\ ...
- 三角関数の積・累乗を組み合わせた積分２前回はこちら： やり方は前回と同様ですので、前回の記事を読まれた方は、本記事を読まずともできるかもしれません。 (1a)を示します。(1a)を $a_n$ と定義すると階差をとって\begin{ali ...
- 三角関数の積・累乗を組み合わせた積分本記事で扱う積分を次のように定義します。 積分の計算にはいくつかのアプローチがあります。 こちらで示した、$s>0$ で成り立つ等式\begin{equation}\int_0^\frac{\p ...
- logを含む難しい積分14（調和数・重積分の応用）前回は： 調和数がらみの級数シリーズはこちら： こちらの「2024/6/29」より $x\le 1$ に対して\begin{equation}\int_0^x\frac{t\ln(1-t)}{1+t^ ...
- Ahmed's IntegralNahin [1] で紹介されている方法を解説します。1つ目の積分を$$I:=\int_0^1\frac{\arctan\sqrt{2+x^2}}{(1+x^2)\sqrt{2+x^2}}dx$$と定 ...
- logを含む難しい積分13（Euler-sumの応用,weight5）前回： $$I:=\int_0^1\frac{\ln^3x\ln(1-x)}{1+x}dx$$について、$\ln(1-x)$ と $\frac{1}{1+x}$ を級数展開します。$$I=\sum_{ ...
- ヤコビの楕円関数を含む積分ヤコビの楕円関数については： タイトルにある積分として最も簡単な積分をやってみましょう。まずは$$I_1 :=\int \sn u \:du$$$\sn u$ は母数も明示するなら $\mathrm{ ...
- ある4F3の特殊値と逆三角関数および対数正弦積分Brychkov[1]の初等関数の定積分を眺めていると なる公式がありました。過去に得られた知見に基づけば、これの証明は難しくありません。 $\arccos x=\frac{\pi}{2}-\arcs ...
- 楕円積分がみたす微分方程式とルジャンドルの関係式・singular value第1種完全楕円積分と第2種完全楕円積分が満たすルジャンドルの関係式を導出します。その際、これらの楕円積分が満たす微分方程式を利用します。またsingular valueについても解説。
- Integrals and Miscellaneous 20.
- 完全楕円積分と算術幾何平均・上昇/下降変換第1種および第2種完全楕円積分と算術幾何平均の関係からスタートし、それを用いて上昇変換と下降変換を導出します。導関数や級数展開についても紹介。
- 楕円積分の導入とその計算方法２(ルジャンドル・ヤコビの標準形)楕円積分はすべて、初等関数と第1,2,3種楕円積分の線型結合で書かれる（ルジャンドル・ヤコビの標準形）ことを示す。
- 楕円積分の導入とその計算方法１有理関数中に4次多項式の無理函数があるものは、一般的に初等関数の範囲では積分できません。一見、無数のパターンがあってどうにもならなそうなこの積分は、実は数パターンに分類できて、その先に面白い世界が広がっています。
- 二重のlogを含む積分２(複素解析・偏角に注意！)被積分関数が２つの複素対数を含むときの、留数定理の活用。
- Integrals and Miscellaneous 19.
- Frullani積分とRamanujanによる一般化フルラニ積分とラマヌジャンによるその拡張について解説。Master theoremを応用します。
- Ramanujan's Master Theoremの留数定理による導出$$\int_0^\infty x^{s-1}\sum_{n=0}^\infty \phi(n)(-x)^n dx=\frac{\pi}{\sin\pi s}{\phi(-s)}$$ラマヌジャンによるメリン変換に関する公式を留数計算によって導出する。
- Integrals and Miscellaneous 18.
- logを含む難しい積分12(超幾何関数の微分の応用)$$\int_0^1\frac{\ln(1-x)}{\sqrt{x-x^3}}dx=\frac{\G^2(\frac{1}{4})}{4\sqrt{2\pi}}\left(\ln2-\pi\right)$$超幾何関数およびそのパラメータによる微分を用いて計算する。
- Integrals and Miscellaneous 17
- logを含む難しい積分11(調和数とEuler sumの利用)$$\int_0^x\frac{\ln^2u\ln^2(1-u)}{u}du$$Euler-sumと深い関係がある積分を導出。非常にテクニカルだが、ほぼ初等的で、さまざまな系を得る。
- logを含む難しい積分10(調和数・アーベルの級数変形法)$$\int_0^1 x^{n-1}\ln^3(1-x)dx=-\frac{H_n^3+3H_nH_n^{(2)}+2H_n^{(3)}}{n}$$対数のマクローリン展開、調和数の利用、アーベルの級数変形法の利用により計算する。Euler-sumの有限和バージョンを扱う。
- Integrals and Miscellaneous 16Previous posts: NEXT:
- logを含む難しい積分９$$\int_0^1\frac{x\ln(1\pm x)}{1+x^2}dx$$調和数および交代調和数の公式を使う方法と、重積分に直して対称性を利用して解く方法を解説。
- Integrals and Miscellaneous 15
- ポリログを含む積分2（重積分・級数展開）$$\int_0^1\frac{x\ln^nx\Li_{n+1}(x)}{1+x^2}dx$$ポリログの積分表示によって重積分へ帰着させ、対称性をうまくもちいて計算する。
- ポリログを含む積分1（重積分・級数展開）$$\int_0^1\frac{\ln^nx\Li_{n+1}(x)}{1+x}dx$$ポリログの積分表示によって重積分へ帰着させ、対称性をうまくもちいて計算する。
- Integrals and Miscellaneous 14Previous posts: Next post:
- 複２次式の平方根を含む積分（楕円積分の応用）$$\int_0^\infty\frac{dx}{\sqrt{x^4+21x^2+112}}=\frac{\G(\frac{1}{7})\G(\frac{2}{7})\G(\frac{4}{7})}{8\sqrt{7}\pi}$$分母が複2次式の平方根となる関数の積分は、第1種楕円積分で表される。ガンマ関数等で閉じた形で表せるものを特に見ていこう。
- Integrals and Miscellaneous 13
- 双曲線関数を含む難しい積分１$$\int_0^\infty\frac{dx}{\sqrt[4]{7+\cosh x}}=\left(\frac{2}{27}\right)^\frac{1}{4}\frac{\G(\frac{1}{4})^2}{\sqrt{\pi}}$$ガウスの超幾何関数を駆使しよう。
- 二重のlogを含む積分１(ゼータ関数の微分)$$\int_0^1\ln\ln\left(\frac{1+\sqrt{1-x^2}}{x}\right)dx$$級数表示し、フルヴィッツゼータ関数の特殊値と、その微分係数を使って計算する。逆双曲線関数にも関りがある。
- logを含む難しい積分８$$\int_0^\infty\frac{\arctan^2x\ln^2(1+x^2)}{x^2}dx$$複素積分を通してlogだらけの６つの実数積分を得る。交代調和数や二重対数関数を駆使して計算しよう。
- Integrals and Miscellaneous 12
- 複素積分演習（真性特異点）$$\int_0^\pi \exp(e^{\cos x}\cos\sin x)\cos(e^{\cos x}\sin\sin x)dx=\pi e$$うまく積分を変形し、留数積分に持ち込む。真性特異点の留数を求める簡単な例。
- 複素積分演習（logの分岐点と切断）留数定理と分岐点を応用する積分2題を解説する。
- logを含む難しい積分７（arcsinhの利用）$$\int_0^a \frac{x^{-\frac{1}{2}}}{\sqrt{1+b^2\sqrt{x(a-x)}}}\ln\left(b\sqrt[4]{x(a-x)}+\sqrt{1+b^2\sqrt{x(a-x)}}\right)dx$$などを計算しよう。
- Integrals and Miscellaneous 11
- logを含む難しい積分６（4F3・楕円積分・二重対数関数）$$\int_0^a x^{s-1}(a-x)^{t-1}\ln\left(b\sqrt{x(a-x)}+\sqrt{1+b^2x(a-x)}\right)dx$$arcsinhとその級数表示により4F3が現れるが、ときに3F2や2F1で表せる。その場合は楕円積分や二重対数関数を駆使しよう。
- logを含む難しい積分５（超幾何級数3F2）$$\int_0^a x^{s+\frac{1}{2}}(a-x)^s\ln\left(1-b\sqrt{x(a-x)}\right)dx$$一般化された超幾何級数を計算する。
- logを含む難しい積分４（複素積分演習）$$\int_0^\infty \frac{x}{x^2+a^2}\ln\frac{x^2+2bx+c}{x^2-2bx+c}dx = 2\pi\arctan\frac{b}{a+\sqrt{c-b^2}}$$留数定理と分岐点を使う。
- logを含む難しい積分３（超幾何級数）$$\int_0^a x^{s-1}(a-x)^{t-1}\ln\bigl(1-bx(a-x)\bigr)dx$$初等的に求まるものから超幾何級数、さらには一般化された超幾何級数を用いたものまで、計算手法は様々である。
- logを含む難しい積分２（級数展開）$$\int_0^1\frac{(1-x)^{s-1}\ln(1-x)}{(1-xz)^{s+1}}dx=-\frac{1}{s(1-z)}\sum_{n=0}^\infty\frac{z^n}{s+n}$$log(1-x)を含む困難な積分について、二項級数に展開してベータ関数を用いて計算する。
- logを含む難しい積分（調和数の4倍添え字を応用）$$\int_0^1\frac{x\ln(1-x)}{1+x^4}dx=\frac{\pi}{32}\ln2-\frac{G}{4}-\frac{\pi}{8}\ln(\sqrt{2}+1)$$級数展開によって計算する。その際、調和数の4倍添え字が現れるため、少々煩雑な計算を要する。
- Integrals and Miscellaneous 10Previous posts: Next:
- 複素積分演習（対数と２つの分岐点）$$\int_0^1\frac{\sqrt{x}\ln(1-x)}{1+x^3}dx=-\frac{2}{9}G-\frac{\pi}{6}\ln2$$分岐点が２つある積分を行う。また級数展開する手法および副産物として現れる奇調和数を含む級数を導出する。
- log(sinh x)の対数正弦積分（調和数・ポリログ）\begin{eqnarray}\int_0^{\frac{\ln2}{2}}x\ln^2(2\sinh x)dx &=& \frac{1}{2}\Li_4\left(\frac{1}{2}\right)-\frac{7\pi^4}{1440}+\frac{7}{16}\zeta(3)\ln2-\frac{\pi^2}{48}\ln^22+\frac{7}{192}\ln^42\end{eqnarray}対数正弦積分の $\sinh$ 版。流れは同様。
- log(sin x)の2乗の対数正弦積分（調和数・ポリログ）\begin{eqnarray}\int_0^\frac{\pi}{4} x\ln^2(2\sin x)dx&=&\frac{5}{16}\Li_4\left(\frac{1}{2}\right)-\frac{11\pi^4}{1152}-\frac{\pi G}{8}\ln2\\&&+\frac{35}{128}\zeta(3)\ln2-\frac{11\pi^2}{384}\ln^22\\&&+\frac{5\ln^42}{384}-\frac{\pi}{4}\mathfrak{I}\Li_3(1-i)\end{eqnarray} 多重対数関数を駆使して解いていこう。
- Integrals and Miscellaneous 9.
- x^s・arctan x の定積分We consider the integrals that have the product of $\arctan x$, $x^s$ and $\ln x$. The point is that ...
- x^s・arcsin x の定積分$$\int_0^1 x^s\ln x\arcsin xdx$$ポイントは x^s をsで微分すると ln x が現れるということだ。
- 三角関数の平方根とx^2の積の積分$$\int_0^\frac{\pi}{2}\t^2\sqrt{\tan\t} d\t$$など6種。ベータ関数の逆数の積分表示を微分するという単純だがやや面倒な問題。
- arctan(x)のn乗の積分(フーリエ展開とディリクレベータ関数)$$I_n:=\int_{0}^{1}\arctan^n x dx$$ディリクレのベータ関数やゼータ関数で表現することになる。途中、フーリエ級数展開を用いる。
- Anger関数とWeber関数①(sinやcosの中にsinがある積分)\begin{eqnarray}\mathbf{J}_\nu(z) &=& \frac{1}{\pi}\int_0^\pi\cos(\nu\t-z\sin\t)d\t\\ \mathbf{E}_\nu(z) &=& \frac{1}{\pi}\int_0^\pi\sin(\nu\t-z\sin\t)d\t\end{eqnarray}を超幾何級数で表す。
- Integrals and Miscellaneous 8積分、級数、その他 小記事集合体。
- Integrals and Miscellaneous 7.
- 複素積分演習 cosx と e^-xの混合（4分円の周回積分）$$\int_0^\infty\frac{\cos ax-e^{-ax}}{x(x^4+b^4)}dx\quad,\quad\int_0^\infty\frac{\sin ax}{x(x^4+b^4)}dx=\frac{\pi}{2b^4}\left(1-e^{-\frac{ab}{\sqrt{2}}}\cos\frac{ab}{\sqrt{2}}\right)$$四分円をうまく用いた複素積分。直線2本が当該の積分にあたり、２つの円弧は適切に計算する必要がある。
- 4次の多重対数関数を応用する積分$$\int_0^x\frac{\ln^2t\ln(1-t)}{1-t}dt$$はどのように表されるだろうか？$Li_4(x)$を繰り返し部分積分して現れる式を活用して困難な積分を導出する。多重対数関数の定義や簡単な関係式を前提とする。
- arctan(μsin x)とarctan(μcsc x)の積分（二重対数関数と黄金比）$$I(s):=\int_0^\frac{\pi}{2}\arctan(s\csc x)dx$$$$J(s):=\int_0^\frac{\pi}{2}\arctan(s\sin x)dx$$と$s=1,2$での値を計算する。二重対数関数を用いる。最後は黄金比がカギとなる。
- Integrals and Miscellaneous 6.
- x^m/(sin x)^nの積分（logsinのフーリエ展開・ディリクレのベータ関数）多項式をsin xの累乗で割った関数を定積分する。１つを除いて初等的に計算できず、ゼータ関数やディリクレのベータ関数を用いて表現することになる。途中、logsinなどのフーリエ展開を用いる。
- x^3/(sinx)^3の積分（ディリクレベータ関数・カタラン定数）$$\int_0^\frac{\pi}{2}\frac{x^3}{\sin^3x}dx=-\frac{3}{8}\pi^2+\left(6+\frac{3}{4}\pi^2\right)G-6\beta(4)$$部分積分によりあえてばらばらにし、級数展開等によってそれぞれ積分を実行する。カタラン定数やディリクレのベータ関数が登場。
- Integrals and Miscellaneous 5.
- コサインの実数乗(cosθ)^μをフーリエ級数展開（ベータ関数の逆数の積分表示を応用）$$\cos^\mu x=\frac{\G(\mu+1)}{2^{\mu-1}\G(\frac{\mu}{2}+1)^2}\left[\frac{1}{2}+\frac{\mu}{\mu+2}\cos2x+\frac{\mu(\mu-2)}{(\mu+2)(\mu+4)}\cos4x\cdots\right]$$前回のベータ関数の知識を生かして導出する。
- 複素積分演習 log(2-2cos x^2) ～フレネル積分の応用～$$I_p\equiv \int_{0}^\infty\ln(2-2\cos x^p)dx$$をフレネル積分に似た複素解析で計算する。
- 重積分を双曲線関数で置換する積分３つ$$\int_0^\infty[\mathrm{arcsinh}(\cosh x)-x]dx=\frac{\pi^2}{16}$$他２つ。ゼータ関数と結びついた重積分を計算することで複雑な定積分の値を求める。重積分の変数を双曲線関数に置換し、座標軸を回転させる。
- Integrals and Miscellaneous 4Various formulas
- 指数関数を含む積分演習 ： 3F2(1)型の超幾何級数とトマエの関係式$$I\equiv\int_0^\infty\frac{xdx}{(e^x-1)^\frac{2}{3}}$$2通りの解法を示す。１つはベータ関数の微分を用いる方法、もう１つは一般化された超幾何関数を計算する方法です。
- 複素積分演習(arctan z/z(1+z^4))複素関数としてのarctanの扱いおよび分岐点、留数定理、鍵穴経路による積分など、いろいろな要素を使って学べる積分例題。
- Integrals and Miscellaneous 3Integrals and Miscellaneous
- アベル・プラナの和公式のバリエーション（複素積分・cotでなくtanで導出する）\begin{multline}\sum_{k=m}^{n-1}f\left(k+\frac{1}{2}\right)=\int_m^nf(x)dx\\+i\int_0^\infty\frac{f(m-iy)-f(m+iy)-f(n-iy)+f(n+iy)}{e^{2\pi y}+1}dy\end{multline}アベル・プラナの和公式を導出したときと似た方法で導こう。複素解析を用いる。
- 複素積分演習（cos(log x)/(1+x^2)）$$I=\int_0^1\frac{\cos\log x}{1+x^2}dx$$複素解析によって計算する。
- Integrals and Miscellaneous 2.
- Excercise of Contour Integral (Combination of Real and Imaginary Axis)Thanks to @AlbahariRicardo : Considering $e^{iz}$, we can see that $e^{ix}$ appears on the real axis ...
- Integrals and Miscellaneous 1Integrals and Miscellaneous 1
- アベル・プラナの和公式 複素積分を応用して\begin{multline}\sum_{k=m}^nf(k)=\frac{f(m)+f(n)}{2}+\int_m^nf(z)dz\\+i\int_0^\infty\frac{f(m+iy)-f(m-iy)-f(n+iy)+f(n-iy)}{e^{2\pi y}-1}dy\end{multline}ビネの第2公式を示すための補題として取り組んだ。複素解析を用いる。
- $\int\sqrt{1+x^n}dx$（超幾何関数）$$\int^1_0\sqrt{1+x^n}dx=F\left(\frac{1}{n},-\frac{1}{2},\frac{1}{n}+1;-1\right)$$$n\ge 3$ においては初等的に解けないが、ガウスの超幾何関数を用いて表すことができる。
- $\int\frac{x^m}{\sinh x}dx,\int\frac{x^m}{\cosh x}dx$ ゼータとベータ$$\int_0^\infty\frac{x^m}{\sinh x}dx\;,\;\int_0^\infty\frac{x^m}{\cosh x}dx$$ガンマ関数と４つのゼータ系関数を使って導く。厳密値が得られる場合とそうでない場合が半々。
- 第1種変形ベッセル関数の積分表示$$I_n(z)=\frac{1}{\pi}\int_0^\pi e^{z\cos\t}\cos n\t d\t=\frac{(z/2)^\nu}{\sqrt{\pi}\G(\nu+\frac{1}{2})}\int_0^\pi e^{\pm z\cos\t}\sin^{2\nu}d\t$$母関数や複素積分、ベータ関数を用いて２つの積分表示を導出する。第1種ベッセル関数 $J_\nu(z)$ の積分表示を導出した記事と方法は酷似している。
- $\int\frac{dx}{(1+x^2)^{n+1}}$ 複素積分演習$$\int_{-\infty}^\infty\frac{dx}{(1+x^2)^{n+1}}=\frac{\pi(2n)!}{(n!)^2\cdot 2^{2n}}$$$n$ 位の極をもつ関数の複素積分を解説．ガウス平面上に半円の閉曲線をとる．初等的にも計算可能．
- Definite integral of √cos x , √sin x (with Gamma function)-integration sqrt(cos x),sqrt(sin x)$$\int_0^\frac{\pi}{2} \sqrt{\cos x}dx\;,\;\int_0^\frac{\pi}{2} \sqrt{\sin x}dx$$There is no elementary solution but we can write the answer with gamma function.
- 三角関数の有理関数と複素積分$$\int_0^{2\pi}\frac{dx}{3+2\sin x} =\frac{2\pi}{\sqrt{5}}$$以前ワイエルシュトラス置換で扱った積分を複素積分で解く。複素平面上で単位円に置換しよう。
- $\int e^{-x^n}\sin(x^n)dx$ の積分（ガンマ関数）$$\int_0^\infty e^{-x^n}\sin(x^n)dx$$特殊な定積分の値を考察する。この積分は過去に見た積分の考え方を応用して解ける。その際ガンマ関数が登場する。
- e^{-x^n} の積分(ガンマ関数と極限操作)$e^{-x}$ の積分は高等学校で学習し、$e^{-x^2}$ の積分も「ガウス積分」としてよく知られています。では $e^{-x^3}\;,\;e^{-x^4}\cdots$ の場合はどうでしょう ...
- 【複素解析】cos(x^n),sin(x^n) の定積分（フレネル積分を一般化）$$\int^\infty_0\cos (x^n)dx\;,\;\int^\infty_0\sin (x^n)dx$$複素積分によって求めたフレネル積分を一般化して考えることによって、求める積分値はガンマ関数を用いて表現できることが分かる。扇形の経路で積分する。
- 【複素解析】cos(x^3),sin(x^3)の積分(扇形周回積分とガンマ関数)$$\int^\infty_0\cos (x^3)dx\;,\;\int^\infty_0\sin (x^3)dx$$フレネル積分を一般化して考える。この積分値は複素積分によりガンマ関数を用いて表現できる。またこの積分はエアリー関数の特殊な場合としても現れることを補足する。
- 【複素解析】フレネル積分-三角関数の特殊な積分 sin x^2 , cos x^2$$\int^\infty_0\cos (x^2)dx\;,\;\int^\infty_0\sin (x^2)dx$$フレネル積分とよばれており、複素解析によって求めることができる。コーシーの積分定理を使うなどの複素積分の練習としてうってつけである。
- $\int\sqrt[n]{\tan x}dx$ とベータ関数$\displaystyle\int_0^{\frac{\pi}{2}}\sqrt[n]{\tan x}dx$ を論じる。$\cos$ と$\sin$ のときは初等的には解けずガンマ関数を使わざるを得なかった。しかし今回は初等的に意外ときれいな式が現れる。まずは正攻法でゴリゴリと積分を試し、さらにベータ関数を用いた方法で導こう。
- $\int\sqrt[n]{\cos x}dx$ の計算 (ガンマ関数,ベータ関数)定積分 $\displaystyle\int_0^{\frac{\pi}{2}}\sqrt[n]{\cos x}dx$ を論じる。初等的には解けないが、ベータ関数とガンマ関数が登場する。
- $\int\sqrt{\cos x}dx$とガンマ関数・ベータ関数$\displaystyle\int_0^{\frac{\pi}{2}}\sqrt{\cos x}dx$ を計算します。初等的に積分できませんが、ベータ関数・ガンマ関数で表すことができます。テイラー展開やガウスの超幾何級数にも触れて多くを学びながら結果にたどり着きます。
- 第1種ベッセル関数の積分表示(2) ポアソンの公式の導出$$\int^\pi_0\cos(z\cos\theta)\sin^{2\nu}\theta d\theta=\frac{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}{(z/2)^\nu}J_\nu(z)$$N次元グリーン関数を求める際に用いた、ベッセル関数のとある積分表示について論じます。
- ワイエルシュトラス置換（三角関数の有理式を積分）$$\int_{0}^{2\pi}R(\cos x,\sin x)dx=\int^\infty_{-\infty}R\left( \frac{1-t^2}{1+t^2},\frac{2t}{1+t^2} \right)\frac{2dt}{1+t^2}$$被積分関数が三角関数の有理式になっている場合の強力な切り札について紹介。初等的な範囲の積分。
- 第1種ベッセル関数の積分表示とその導出$$J_n(x)=\frac{1}{\pi}\int^\pi_0\cos(x\sin\theta-n\theta)d\theta$$$$J_n(x)=\frac{1}{\pi i^n}\int^\pi_0e^{ix\cos\theta}\cos n\theta d\theta$$ベッセルの微分方程式の解「第1種ベッセル関数」の積分表示であるBesselの積分表示およびHansen-Besselの公式の２つを複素積分により導出する。
- ∫(logsin x)^n dx , ∫(logcos x)^n dx -対数正弦積分その３$$\int_0^\frac{\pi}{2}\log^n\sin xdx\;,\;\int_0^\frac{\pi}{2}\log^n\cos xdx$$は厳密に求めることができる。ベータ関数を置換して三角関数を出現させると、微分するたびに$\log\sin$や$\log\cos$が出てくる。あとはディガンマ関数・ポリガンマ関数・ゼータ関数を駆使しよう。
- 対数正弦積分その2 ∫(logsin x)^2dx$$\int_0^\frac{\pi}{2}(\log\sin x)^2dx\;,\;\int_0^\frac{\pi}{2}(\log\cos x)^2dx$$は厳密に求めることができる．ベータ関数を置換して三角関数を出現させると，微分するたびに$\log\sin$や$\log\cos$が出てくる．後はポリガンマ関数などを駆使しよう．
- ∫logsin xdx 対数正弦積分その1$$\int_0^\frac{\pi}{2}\log\sin xdx\;,\,\int_0^\frac{\pi}{2}\log\cos xdx$$を初等的に求める．また，より一般的な対数正弦関数へ拡張するためにベータ関数などの特殊関数を用いた解法も解説．